
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фундаментальные колебательные спектрыСодержание книги
Поиск на нашем сайте
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ
А.М. Ефимов ОПТИЧЕСКИЕ СВОЙСТВА Материалов
Санкт-Петербург Ефимов А.М. Оптические свойства материалов и механизмы их формирования. – СПб: СПбГУИТМО., 2008. – 103 с.
Настоящее издание представляет собой учебное пособие к образовательному модулю ОПД.Ф.07 «Оптическое материаловедение» бакалаврской программы «Фотоника и оптоинформатика». Учебное пособие предназначено для студентов, обучающихся по бакалаврскому направлению «Фотоника и оптоинформатика». Материал может быть также рекомендован для студентов, обучающихся по магистерскому направлению «Оптические материалы фотоники и оптоинформатики».
Рекомендовано УМО по образованию в области приборостроения и оптотехники в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению подготовки 200600 - «Фотоника и оптоинформатика».
В 2007 году СПбГУ ИТМО стал победителем конкурса инновационных образовательных программ вузов России на 2007–2008 годы. Реализация инновационной образовательной программы «Инновационная система подготовки специалистов нового поколения в области информационных и оптических технологий» позволит выйти на качественно новый уровень подготовки выпускников и удовлетворить возрастающий спрос на специалистов в информационной, оптической и других высокотехнологичных отраслях экономики.
© Санкт-Петербургский государственный университет информационных технологий, механики и оптики, 2008. © Ефимов А.М. 2008. В 2007 году СПбГУ ИТМО стал победителем конкурса инновационных образовательных программ вузов России на 2007–2008 годы. Реализация инновационной образовательной программы «Инновационная система подготовки специалистов нового поколения в области информационных и оптических технологий» позволит выйти на качественно новый уровень подготовки выпускников и удовлетворить возрастающий спрос на специалистов в информационной, оптической и других высокотехнологичных отраслях экономики.
1994 г. Организована базовая кафедра СПбГУ ИТМО при Государственном оптическом институте (ГОИ) им. С.И.Вавилова – кафедра оптического материаловедения. Образование кафедры явилось логичным развитием тесных связей, которые в течение многих лет существовали между ГОИ и ИТМО. В частности, для преподавания в ИТМО широко привлекались ведущие сотрудники ГОИ, а ИТМО был постоянным источником, из которого ГОИ черпал новые молодые кадры. Кафедра начала подготовку специалистов по образовательному направлению «Оптотехника», специальность «Оптические технологии и материалы». 1999 г. Реорганизация кафедры. На кафедре созданы три направления: оптическое материаловедение, информационная оптотехника, физическая оптика и спектроскопия. Кафедра переименована в кафедру оптического материаловедения и оптики (ОМиО). 2002 г. Кафедра ОМиО вошла в состав нового факультета СПбГУ ИТМО - фотоники и оптоинформатики. 2003 г. При кафедре создана учебно-исследовательская лаборатория материалов и технологий фотоники. 2004 г. Кафедра явилась одним из инициаторов и организаторов создания нового образовательного направления подготовки бакалавров и магистров – «Фотоника и оптоинформатика». Кафедра начала подготовку бакалавров и магистров по направлению - 200600 «Фотоника и оптоинформатика». 2005 г. Кафедра ОМиО переименована в кафедру оптоинформационных технологий и материалов (ОТиМ). 2006 г. Кафедра ОТиМ – лидер в России по подготовке специалистов по оптическому материаловедению в области фотоники и оптоинформатики. Кафедра ведет совместные научные исследования с зарубежными компаниями Corning, Samsung, PPG Inc. 2007 г. Первый выпуск бакалавров по направлению «Фотоника и оптоинформатика». 2008 г. Второй выпуск бакалавров по направлению «Фотоника и оптоинформатика». Содержание Введение Основные понятия физики оптических явлений в твердых телах 1.1. Общие соотношения 1.2. Виды и механизмы поглощения электромагнитного излучения в различных спектральных диапазонах 1.2.1. Фундаментальное поглощение, обусловленное возбуждениями в твердых телах 1.2.1.1. Формирование электронных спектров твердого тела в одноэлектронном приближении 1.2.1.2. Фундаментальное электронное поглощение в диэлек-триках Литература Введение Начиная знакомство с данным разделом дисциплины "Оптическое материаловедение", студентам нужно иметь в виду, что этот раздел предполагает наличие у них некоторого базового объема знаний по смежным естественнонаучным дисциплинам (таким, как, например, «Физика твердого тела»). Необходимость таких исходных базовых знаний обусловлена тем, что при изложении всех вопросов от самых истоков непосредственно в данном разделе дисциплины объем этого раздела превысил бы все разумные рамки. При этом следует также учитывать, что любые названия конкретных дисциплин являются достаточно условными. В природе не существует жестких разграничительных линий между различными классами явлений. Поэтому, например, в средние века, когда весь имеющийся объем знаний о естественных науках еще мог быть охвачен и проанализирован мозгом одного человека, не возникало и необходимости как-то разграничивать эти науки друг от друга, и все они обозначались единым термином – натурфилософия. По мере развития естественных наук исследователи оказались вынужденными проводить какие-то разграничительные линии, чтобы структурировать все возрастающий объем знаний и получить возможность специализироваться в тех или иных направлениях. Естественно, эти разграничительные линии и, соответственно, названия конкретных дисциплин менялись и продолжают меняться с течением времени. Например, первое издание всеобъемлющей монографии Роберта Вуда, вышедшее в 1909 г., называлось «Физическая оптика»: в то время понятие «Физическая оптика» включало в себя почти все, что к тому времени было известно существенного обо всем классе оптических явлений (включая вопросы, выделившиеся позднее в направление «Спектроскопия»). Вышедшая в 1967 г. монография Макса Гарбуни «Оптическая физика» (в русском переводе – «Физика оптических явлений» [1]) снова освещает, несмотря на различие названий, тот же круг общих вопросов, что и монография Роберта Вуда, отражая при этом уже значительно более поздний этап развития данной области науки и включая ряд новых аспектов. Современное же содержание термина «Оптическая физика» (как можно видеть, например, по дисциплине, обозначаемой этим термином в действующей учебной программе естественнонаучного цикла) стало существенно более узким по части изложения общих вопросов, но зато затрагивает многие новые направления, еще только появившиеся или даже просто не существовавшие во времена Макса Гарбуни. Ввиду такой условности границ между различными смежными дисциплинами некоторые исходные моменты излагаемых ниже вопросов (включая математические соотношения) неизбежно перекликаются с теми, которые представлены и в других дисциплинах (например, в тех же дисциплинах естественнонаучного цикла «Физика твердого тела» и «Оптическая физика»). Присутствие ряда таких общих исходных моментов в данном разделе необходимо ради сохранения логической последовательности изложения, так как здесь эти моменты и соотношения развиваются далее и детализируются до уровней, не достигаемых в других дисциплинах. Сравнивая аналогичные исходные уравнения в различных дисциплинах, следует иметь в виду, что набор мировых констант, участвующих в том или ином уравнении, и положение в нем множителя 2 p могут различаться в зависимости от выбора системы единиц. В данном разделе все уравнения приводятся для системы единиц CGSE, так как в системе СИ они были бы более громоздкими из-за необходимости введения дополнительных констант (прежде всего диэлектрической проницаемости вакуума, являющейся в системе СИ размерной величиной в отличие от системы CGSE, где она безразмерна и равна единице). Известно, что в качестве оптических материалов могут использоваться не только твердые тела, но и вещества в других агрегатных состояниях (например, жидкие и газообразные активные среды для некоторых типов лазеров). Однако в подавляющем большинстве случаев оптические материалы являются твердотельными, то есть по своей физической природе они относятся либо к кристаллам, либо к стеклам. Поэтому данный раздел дисциплины посвящен, прежде всего, именно этим классам оптических материалов. Общая схема взаимосвязей между различными группами оптических материалов приведена на рис. 1. Все оптические материалы для удобства последующего рассмотрения можно условно разделить по их практическому применению на две больших группы - пассивные и активные материалы (см. рис. 1). Пассивные оптические материалы служат для передачи световых потоков, несущих энергию излучения или оптическое изображение, и для формирования этого изображения. Активные оптические материалы служат дляуправления световыми потоками и генерации этих потоков. Исторически первые оптические материалы были именно пассивными материалами, а активные материалы возникли позднее. Они разрабатывались, используя имевшиеся пассивные оптические материалы как исходные матрицы для последующей модификации путем введения активаторов (то есть добавок определенных веществ) или направленного создания дефектов, которые придают матрице дополнительные свойства. Поэтому для понимания всей совокупности оптических свойств даже самых сложных современных активных материалов совершенно необходимы глубокие знания в области механизмов формирования оптических свойств пассивных материалов. Основополагающим требованием к пассивным оптическим материалам является оптическая однородность, то есть отсутствие заметных изменений волнового фронта при прохождении через слой материала в произвольно выбранном направлении. Вопрос об оптической однородности ставится принципиально различным образом для кристаллических и стеклообразных материалов. Для кристаллов наличие правильной решетки, обладающей свойством трансляционной симметрии, предопределяет, как известно, неизбежную анизотропию большинства или даже всех их свойств (более подробно данный вопрос уже рассматривался в предшествующем разделе данной дисциплины и затрагивался также в дисциплине естественнонаучного цикла «Физика твердого тела»). Изотропность оптических свойств и соответственно оптическая однородность свойственны лишь кристаллам кубической сингонии, для которых скорости распространения световой волны по трем осям решетки совпадают (тогда как некоторые другие их свойства – например, механические – все же обладают анизотропией). Для стекол, лишенных технологических дефектов, полная изотропность всех их свойств и соответственно оптическая однородность являются, напротив, их характерными отличительными чертами. Это обусловливается такой принципиальной физической особенностью стеклообразного состояния вещества как случайная неупорядоченность его структуры (этот вопрос более подробно затрагивается ниже в параграфе 5.1, а также рассматривается в последующем разделе данной дисциплины). К сожалению, в русскоязычной научной и педагогической литературе отсутствуют какие-либо издания, охватывающие достаточно большую часть тематики данного раздела дисциплины. Известные переводные монографии [1-3] уже не соответствуют современному состоянию науки и к тому же освещают лишь общие вопросы, не затрагивая расчетных методов и задач практического применения оптических материалов. То же самое относится и к хорошо известному учебнику [4]. Поэтому значительная часть необходимого материала оказывается рассеянной по узкоспециализированным монографиям (например, [5-7]) и оригинальным журнальным публикациям, а некоторые вопросы вообще не освещены в русскоязычной литературе. В англоязычной литературе превалируют те же тенденции – с тем исключением, что тематика данного раздела достаточно широко излагается как целое в монографии [8]. Однако эта монография имеется лишь в двух крупнейших научных библиотеках Петербурга и Москвы и поэтому мало доступна студентам. Данное учебное пособие призвано в какой-то мере возместить эти пробелы в имеющейся литературе.
Общая схема взаимосвязей между различными группами оптических материалов. Основные понятия физики оптических явлений в твердых телах Общие соотношения На макроскопическом уровне поведение материала под воздействием электрического поля световой волны определенной частоты описывается в линейном приближении с помощью уравнений Максвелла (см., например, [2]). Уравне́ния Ма́ксвелла (1864 г.) - основные уравнения классической электродинамики, описывающие эволюцию электромагнитного поля и его взаимодействие с зарядами и токами. В данном пособии они подробно не рассматриваются. Чтобы дать общее представление об уравнениях Максвелла, ниже приводится их вид в системе единиц CGSE:
Здесь: · ρ — плотность электрического заряда (в единицах СИ — Кл/м³); · j — плотность электрического тока (в единицах СИ — А/м²); · λ — удельная проводимость или, что то же, электропроводность (в единицах СИ — м/Ом); · E — напряжённость электрического поля (в единицах СИ — В/м); · H — напряжённость магнитного поля (в единицах СИ — А/м); · D — электрическая индукция (в единицах СИ — Кл/м²); · B — магнитная индукция (в единицах СИ — Тл = Вб/м²= кг·с-2·А-1); · rot — дифференциальный оператор ротора; · div — дифференциальный оператор дивергенции. Магнитная и электрическая постоянные вакуума обозначаются через ε0 и μ0. Поэтому для вакуума электрическая и магнитная индукция может быть записана (без учета очень малых квантовых эффектов) в виде
Уравнения Максвелла для вакуума без электрических зарядов и токов имеют вид:
Эта система дифференциальных уравнений имеет простое решение — гармоническая, плоская волна. Векторы электрического и магнитного полей перпендикулярны направлению распространения волны и друг другу, и находятся в фазе. Волна распространяется со скоростью
где c - скорость света в вакууме. Общепринятые значения скорости света, электрической и магнитной постоянных в системе СИ приведены в таблице.
Для понимания дальнейшего изложения данной дисциплины достаточно знать, что, согласно решениям уравнений Максвелла, а) отклик материала на воздействие электрического поля световой волны полностью определяется его диэлектрической проницаемостью при этой частоте; б) диэлектрическая проницаемость материала с любой конечной (не равной нулю) электрической проводимостью (то есть любого материала, кроме вакуума) является комплексной величиной. Таким образом, используя широко распространенное в математике обозначение комплексной величины с помощью значка ˆ над ее символом, можно написать: Поскольку диэлектрическая проницаемость – это всегда квадрат показателя преломления, то показатель преломления также оказывается комплексной величиной
Соответственно e¢ = n 2 - k 2 (1.1.2а) и e¢¢ = 2 n´k. (1.1.2б) Рассмотрим теперь в общих чертах, что происходит в материале на микроуровне при воздействии на него электрической составляющей электромагнитного поля световой волны. Под воздействием приложенного электрического поля световой волны имеющиеся в нем электрические заряды (электроны, ионы и атомы, несущие какие-либо эффективные заряды) смещаются в направлении соответствующих полюсов. Это явление называется поляризацией материала. В результате в нем возникают наведенные диполи (которые добавляются к постоянным диполям, если таковые имелись в материале). Количественной мерой поляризации материала служит вектор поляризации (или, кратко, просто поляризация) Таким образом, действительная и мнимая части комплексной диэлектрической проницаемости (равно как и показателя преломления), которые определяют преломляющие и абсорбционные свойства материала соответственно, не являются независимыми: существует глубокая внутренняя взаимосвязь этих на первый взгляд различных свойств. Эта взаимосвязь подробно рассматривается ниже в подразделах 3-5. Во всех дисциплинах, относящихся к области физики оптических явлений, принято обозначать взаимосвязанные пары величин e¢ и e¢¢ и/или n и k собирательным термином «оптические постоянные». Именно такой смысл термина «оптические постоянные» и используется в данном учебно-методическом пособии.[3] В простейшем случае равенства внешнего (приложенного) электрического поля E и внутреннего электрического поля в материале E int[4] значение вектора поляризации
где N - число заряженных частиц (электронов, атомов или ионов) в единице объема вещества. Комплексный коэффициент пропорциональности Как же связать эту микроскопическую характеристику с вышеописанными характеристиками макромира? Из электростатики известно, что
Приравнивая это выражение и вышеприведенное выражение (3) для P, получаем, что в приближении равенства внешнего и внутреннего электрического поля комплексная диэлектрическая проницаемость выражается через поляризуемость соотношением
До сих пор рассмотрение ограничивалось случаем постоянной частоты световой волны (т. е. случаем монохроматического излучения). Однако оптические постоянные всегда являются, как известно, функциями частоты, что не рассматривается в рамках решений уравнений Максвелла (они являются слишком общими для такого рассмотрения). Поэтому, строго говоря, вышеприведенные выражения для
и
Здесь w - текущая круговая частота, являющаяся аргументом соответствующих функций. Она связана с длиной волны l соотношением w = 2p c/l, где c - скорость света. Наряду с круговой частотой используются и другие характеристики частоты: · линейная частота n (здесь n - греческая буква «ню»; не путать с латинской v!), характеризующая число периодов волны в секунду (размерность – Гц), · n = c/l = w/ 2p; · волновое число
Линейная частота используется, как правило, для волн радиодиапазона, а волновое число – для волн инфракрасного (ИК) диапазона. Для областей очень высоких частот излучение принято характеризовать также энергией кванта E (в эВ):
где h – постоянная Планка, или, при выражении длины волны в мкм,
Прежде чем переходить к анализу частотной зависимости оптических постоянных, необходимо напомнить вкратце физическую природу поглощения оптического излучения в различных спектральных диапазонах, а также количественные соотношения, описывающие изменения характеристик светового потока при прохождении через слой оптического материала. Феноменология Общий вид зависимости показателя преломления и показателя собственного поглощения бесцветных оптических материалов от длины волны в области прозрачности показан на рис. 10. Как видно из рисунка, в области прозрачности показатель преломления нелинейно уменьшается с длиной волны; эту тенденцию принято называть термином «нормальная дисперсия». Примерно к середине области прозрачности скорость этого уменьшения замедляется, а затем начинает снова постепенно возрастать, то есть в центре области прозрачности существует точка перегиба. Примеры зависимостей n = n(l) для кварцевого стекла и халькогенидного стекла ИКС25, существенно различающихся по спектральному положению области прозрачности, приведены на рис. 11. Как видно из рис. 10, собственное поглощение в общем случае быстро спадает при переходе от далекого ультрафиолета к ближнему и далее к видимому диапазону. Оно также спадает при переходе в обратном направлении - от среднего ИК к ближнему ИК и далее к видимому диапазону. Таким образом, при отсутствии поглощающих примесей и собственных дефектов потери света в бесцветных оптических материалах определяются лишь «хвостами» областей собственного электронного и колебательного поглощения, расположенными в вакуумном УФ и среднем ИК диапазонах. Из экспериментов с особо чистыми оптическими волокна-
Рис. 10. Типичный ход зависимости показателя преломления и показателя поглощения от длины волны в области прозрачности материала
ми из кварцевого стекла известно, что точка пересечения этих «хвостов» (и соответственно точка максимально возможного светопропускания) лежит при длине волны около 1.5 мкм. Перейдем теперь к экспериментальной картине дисперсии показателя преломления и показателя собственного поглощения в широком диапазоне длин волн, охватывающем не только область прозрачности, но и диапазоны фундаментального поглощения, иллюстрируемой на примере кварцевого стекла с помощью данных [16] (см. рис. 12). Видно, что за пределами области "нормальной" дисперсии по обе ее стороны лежат области, в которых показатель преломления возрастает с длиной волны. Такие области принято называть областями "аномальной" дисперсии. Существенно отметить, что, как видно на рисунке, положение мощных максимумов собственного поглощения как раз и соответствует центрам областей "аномальной" дисперсии, подтверждая, таким образом, наличие глубокой внутренней взаимосвязи между явлениями поглощения и преломления. Такова степень сложности экспериментальной картины, которую исследо- вателям предстояло не только качественно объяснить с помощью подходящих физических моделей, но и количественно описать наблюдае-
Рис. 11. Примеры зависимостей n = n(l) для (а) кварцевого стекла и (б) халькогенидного стекла ИКС25. Точки – данные разных измерений, линии – аппроксимирующие кривые.
Рис. 12. Полный спектр оптических постоянных стеклообразного кремнезема [16]. мые явления с помощью соответствующих математических уравнений, называемых также аналитическими моделями этих явлений. Метод Крамерса-Кронига Метод Крамерса-Кронига базируется на использовании соотношения Крамерса-Кронига (3.1.5) для фазового угла. Существенно, что это соотношение предусматривает интегрирование от нуля до бесконечности, а экспериментальный спектр отражения
Для первого и третьего интегралов, соответствующих неизмеряемым спектральным диапазонам Например, вид
где C - константа, а показатель степени k подбирается в пределах 3 < k < 4. Уточнение вида модельных функций и значений их параметров производится с помощью привязочных точек, для которых значения фазового угла известны из независимых соображений (например, во всей области высокой прозрачности фазовый угол по определению равен нулю) или измерений. В литературе описано множество версий метода Крамерса-Кронига, различающихся выбором модельных функций, спектральной областью применения и степенью надежности вычисления значений оптических постоянных. Известно, что в целом результаты применения метода Крамерса-Кронига весьма чувствительны к локальным ошибкам анализируемого спектра отражения. Наличие таких ошибок может привести к получению ложных экстремумов в спектрах оптических постоянных. Значения фазового угла, полученные с помощью уравнения (6.2.1), используются вместе со значениями
и
Как и в случае двух предыдущих методов, получаемые с помощью метода Крамерса-Кронига результаты целиком ограничиваются спектрами оптических постоянных. Если исследователю нужно найти не только спектры оптических постоянных как таковые, но также значения частот и интенсивностей полос, перекрывающихся между собой в сложном спектре мнимой части диэлектрической проницаемости, он должен разложить этот спектр на такие индивидуальные полосы с помощью уже какого-то другого, независимого метода разложения. В этом случае итоговая погрешность расчета параметров полос будет равна сумме погрешностей метода вычисления оптических постоянных (в частности, метода Крамерса-Кронига) и метода разложения сложного спектра. Диаграмма Аббе. Для наглядного представления взаимосвязи между основными характеристиками различных оптических материалов Эрнстом Аббе была предложена диаграмма «главный показатель преломления – коэффициент дисперсии», носящая с тех пор его имя. Диаграмма Аббе чрезвычайно удобна для совместного представления всех стекол каталога оптического стекла и других бесцветных материалов и для выбора пар оптических стекол, используемых для ахроматизации оптической системы (см. ниже параграф 7.3). Пример диаграммы Аббе nd - nd для стекол современного каталога фирмы Шотт представлен на рис. 28. Следует обратить внимание, что значения коэффициента дисперсии на диаграмме Аббе возрастают, по традиции, заложенной еще ее автором, справа налево, а не наоборот. При таком выборе координат все бесцветные оптические стекла, известные во временаШотта и Аббе (когда их химические составы базировались лишь на силикатной основе), располагались на этой диаграмме в виде широкой области, вытянутой от нижнего левого угла диаграммы к ее правому верхнему углу. Таким образом, одного взгляда на диаграмму Аббе было достаточно, чтобы увидеть преобладающую тенденцию взаимосвязанного изменения значений двух основных оптических характеристик с химическим составом оптических стекол: с возрастанием главного показателя преломления стекла его коэффициент дисперсии в большинстве случаев уменьшается. На самом начальном этапе развития оптического стекловарения были выделены всего лишь два основных типа оптических стекол: кроны (стекла с высокими значениями коэффициента дисперсии и сравнительно низкими – показателя преломления) и флинты (стекла с низкими значениями коэффициента дисперсии и высокими – показателя преломления). В дальнейшем общее число оптических стекол быстро возрастало, а область, занимаемая ими на диаграмме Аббе, непрерывно увеличивалась.[18] По мере расширения номенклатуры оптических стекол потребовалось вводить новые их типы и соответственно делить диаграмму Аббе на большее число специфических участков. Прежние кроны распались на легкие кроны, кроны, тяжелые кроны и сверхтяжелые кроны. Прежние флинты распались на легкие флинты, флинты, тяжелые флинты и сверхтяжелые флинты. Между легкими кронами и легкими флинтами появилась группа кронфлинтов. Однако вскоре и этого разнообразия типов оказалось недостаточно. В целях достижения либо предельно высоких значений коэффициента дисперсии, либо высоких значений одновременно и показателя преломления, и коэффициента дисперсии разработка стекол новых составов велась в основном путем использования несиликатных матриц (боратной, фосфатной, фторидной и некоторых других) и ряда новых компонентов (таких, как окислы лантана, тантала, титана). Новые типы стекол стали обозначаться с привлечением названий химических элементов, окислы которых придают им свою специфику. Последняя тенденция ярко проявляется для стекол каталога фирмы Шотт: на соответствующей диаграмме Аббе (см. рис. 28) можно видеть области
Рис. 28. Диаграмма Аббе для стекол современного каталога фирмы Шотт. стекол типов FK (фторидных кронов), PK и PSK (фосфатных кронов), BaK, BaLF и BaSF (кронов, легких и тяжелых флинтов, содержащих окись бария), LaK, LaF и LaSF (кронов, флинтов и тяжелых флинтов, содержащих окись лантана).[19] Для стекол на несиликатных основах характерны несколько иные, чем в случае силикатных стекол, сочетания главного показателя преломления и коэффициента дисперсии. В результате область, занимаемая оптическими стеклами на современных диаграммах Аббе (см. рис. 28), существенно расширилась, и поэтому вышеупомянутая тенденция уменьшения коэффициента дисперсии с возрастанием главного показателя преломления стала проявляться не столь ярко. В настоящее время достигнутые пределы значений nd и nd промышленных оптических стекол составляют примерно 17 - 95 и 1.43 - 2.17 соответственно. Крайние значения nd» 95 при nd» 1.43 и nd» 17 при nd» 2.17 относятся к стеклу N-FK56 из каталога фирмы Шотт 1996 года и к российскому стеклу СТФ3 (в настоящее время снятому с производства) соответственно. Для изотропных оптических кристаллов нижний предел соответствует кристаллу фтористого лития (nd» 99 при nd» 1.39) а для анизотропных (одноосных) - кристаллу фтористого магния (для обыкновенного луча nd» 106 при nd» 1.38). Диаграммы типа Аббе могут строиться и для материалов, прозрачных в других частотных диапазонах, с соответствующим изменением опорных длин волн для выбора главного показателя преломления и средней дисперсии. В частности, для халькогенидных оптических стекол используются диаграммы типа Аббе в координатах n 2.0- n 2.0, n 4.0- n 4.0и n 10.0- n 10.0(см. [8]), где подстрочные индексы указывают длину волны в мкм, а именно: n 2.0= (n 2.0- 1)/(n 1.8- n 2.2); n 4.0= (n 4.0- 1)/(n 3.0- n 5.0); n 10.0= (n 10.0- 1)/(n 8.0- n 12.0). Литература [1] Гарбуни М. Физика оптических явлений, М.: Машиностроение, 1967. – 517 с. [2] Борн М., Вольф Э. Основы оптики. - М.: Наука, 1970. – 855 с. [3] Мосс Т.С. Оптические свойства полупроводников. М.: Наука, 1965. – 317 с. [4] Ландсберг Г.С. Оптика. Л.: Наука, 1982. – 615 с. [5] Бонч-Бруевич В.Л., Звягин И.Р., Кайпер Р., Миронов А.Г., Эндерлин Р., Эссер Б. Электронная теория неупорядоченных полупроводников, М.: Наука, 1981. – 377 с. [6] Филлипс Дж. Оптические спектры твердых тел. М.: Наука, 1970. – 287 с. [7] Накамото К. Инфракрасная спектроскопия. М.: Наука, 1970. – 287 с. [8] Efimov A.M. Optical Constants of Inorganic Glasses. Boca Raton, N. Y., etc.: CRC Press, 1995. – 202 с. (chaps. 1-3, 5). [9] Mott N.F., Davis E.A. Electronic Processes in Non-Crystalline Materials. Oxford: Clarendon Press, 1979. – 604 p. [10] Соболев В.В. Экситонные спектры MgO. // Неорганические Материалы. – 2004. – Т. 40. – № 11. – С. 1333-1336. [11] Силинь А.Р., Трухин А.Н. Точечные дефекты и элементарные возбуждения в кристалл
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 527; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.89.181 (0.016 с.) |


 Учебное пособие
Учебное пособие

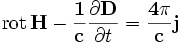








 ,
,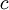


 .
. , в которой действительная часть n – это знакомый всем из школьного курса физики показатель
, в которой действительная часть n – это знакомый всем из школьного курса физики показатель  . (1.1.1)
. (1.1.1) - суммарный наведенный дипольный момент [2] единицы объема. Наличие не равного нулю поглощения энергии световой волны в материале вызывает отставание вектора поляризации
- суммарный наведенный дипольный момент [2] единицы объема. Наличие не равного нулю поглощения энергии световой волны в материале вызывает отставание вектора поляризации  по фазе от внешнего электрического поля этой волны Е, что и приводит к необходимости описания вектора поляризации и диэлектрической проницаемости (а, следовательно, и показателя преломления) как комплексных величин.
по фазе от внешнего электрического поля этой волны Е, что и приводит к необходимости описания вектора поляризации и диэлектрической проницаемости (а, следовательно, и показателя преломления) как комплексных величин. определяется соотношением
определяется соотношением , (1.1.3)
, (1.1.3) между приложенным полем и вкладом в значение вектора поляризации называется поляризуемостью соответствующей частицы вещества. Таким образом, поляризуемость служит микроскопической характеристикой поляризации.
между приложенным полем и вкладом в значение вектора поляризации называется поляризуемостью соответствующей частицы вещества. Таким образом, поляризуемость служит микроскопической характеристикой поляризации. . (1.1.4)
. (1.1.4) . (1.1.5)
. (1.1.5) и
и  следует переписать в виде
следует переписать в виде (1.1.6)
(1.1.6) . (1.1.7)
. (1.1.7)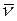 (его размерность – см-1):
(его размерность – см-1):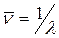 .
. ,
,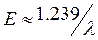 .
.



 , подлежащий обработке, всегда известен только в конечном (притом обычно не слишком широком) диапазоне частот. Поэтому процедура вычислений строится на разбиении интеграла в (3.1.5) на три, средний из которых имеет конечные пределы и соответствует измеренному диапазону частот
, подлежащий обработке, всегда известен только в конечном (притом обычно не слишком широком) диапазоне частот. Поэтому процедура вычислений строится на разбиении интеграла в (3.1.5) на три, средний из которых имеет конечные пределы и соответствует измеренному диапазону частот  :
: 6.2.1)
6.2.1) и
и  , должны быть подобраны какие-то подходящие модельные функции
, должны быть подобраны какие-то подходящие модельные функции  и
и 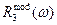 , задающие ожидаемую дисперсию
, задающие ожидаемую дисперсию  в этих диапазонах. Предполагаемый вид этих модельных функций и является той независимой дополнительной информацией, которая необходима для решения задачи вычисления оптических постоянных.
в этих диапазонах. Предполагаемый вид этих модельных функций и является той независимой дополнительной информацией, которая необходима для решения задачи вычисления оптических постоянных.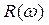 в области энергий свыше 30 эВ часто аппроксимируется степенной функцией вида
в области энергий свыше 30 эВ часто аппроксимируется степенной функцией вида
 для расчета спектров оптических постоянных с помощью формул
для расчета спектров оптических постоянных с помощью формул (6.2.2а)
(6.2.2а) (6.2.2б)
(6.2.2б)



