
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отражение на границе раздела двух сред.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В общем случае произвольного угла падения луча на границу раздела двух сред коэффициент отражения R определяется известными формулами Френеля, согласно которым он является функцией значений оптических постоянных этих двух сред и значения угла падения, а также зависит от поляризации падающего луча (понятие поляризации света предполагается известным студентам).[7] 2.2.1. Отражение на границе раздела двух прозрачных сред Формулы Френеля для отражения на границе раздела двух прозрачных сред имеют следующий вид. Для луча, поляризованного перпендикулярно плоскости падения: R s = Для луча, поляризованного параллельно плоскости падения: R p = Для простейшего случая нормального падения луча из среды c показателем преломления n 1 на границу раздела с полностью прозрачным (непоглощающим) материалом, имеющим показатель преломления n 2, формулы Френеля (2.2.1а) и (2.2.1б) сводятся к одной простой формуле, так как коэффициент отражения R перестает зависеть от вида поляризации падающего луча: R = (n 2 - n 1)2 / (n 2 + n 1)2. (2.2.2а) При нормальном падении луча из вакуума (n 1 = 1) или воздуха (n 1» 1) уравнение (2.1.5) переходит, при обозначении n 2 просто через n, в хорошо известную простейшую формулу R = (n -1)2 / (n +1)2. (2.2.2б) Рассмотрим угловую зависимость коэффициента отражения на примере границы раздела двух прозрачных сред со значениями показателя преломления, равными 1.0 (вакуум или воздух) и 2.0 (см. рис. 9). Как видно из рис. 9, при падении луча из оптически менее плотной среды на поверхность более плотной коэффициент отражения R s (для поляризации перпендикулярно плоскости падения) нелинейно возрастает с увеличением угла падения. Напротив, коэффициент отражения R p (для поляризации параллельно плоскости падения) нелинейно убывает с увеличением угла падения, проходя через глубокий (почти до нуля) минимум при определенном значении угла, называемом углом Брюстера. [8] Для стекла со значением n 2 ≈ 1.5 в воздухе или вакууме значение угла Брюстера составляет примерно 56°.
Рис. 9. Угловая зависимость коэффициента отражения для случаев падения луча (а) из менее плотной среды (вакуум) в более плотную (n 2 = 2.0) и (б) из той же более плотной среды в менее плотную (вакуум).
Такое различное угловое поведение значений R s и R p приводит к тому, что при падении пучка неполяризованного света, характеризуемого коэффициентом отражения R = (R s + R p)/2, отраженный и преломленный лучи оказываются в той или иной степени поляризованными. В отраженном луче преобладает (или, при угле Брюстера, полностью доминирует) s-составляющая поляризации (этот эффект раньше даже использовался на практике для создания поляризаторов за счет многократного отражения). В преломленном луче преобладает p-составляющая поляризации.
Рис. 9 показывает далее, что при падении луча из оптически более плотной среды на поверхность менее плотной общая форма кривых угловой зависимости коэффициентов отражения R s и R p сохраняется. Однако возрастание обоих коэффициентов отражения с увеличением угла происходит гораздо быстрее, и их значения, равные 1.0 (100%) достигаются не при нормальном падении, как в предыдущем случае, а при определенном значении угла падения j << 90°, которое называется критическим углом или углом полного внутреннего отражения.[9] Для стекла со значением n 2 ≈ 1.5 в воздухе или вакууме значение критического угла составляет примерно 41°. 2.2.2. Отражение на границе сильно поглощающего материала Для сильно поглощающего материала (k» n) действительный показатель преломления n во всех вышеприведенных соотношениях должен быть заменен комплексным показателем преломления
Из уравнения (2.2.3) видно, что при k >> n значение R стремится к единице (случай зеркального отражения металлов). Переходя к более детальному рассмотрению отражения на границе сильно поглощающего материала, необходимо уточнить само понятие коэффициента отражения. Тот коэффициент отражения R, который рассматривался выше, более точно именуется термином «энергетический коэффициент отражения». Однако для полной характеристики отраженного луча необходимо знать не только его энергию, но и его фазу. Дело в том, что фаза отраженного луча остается неизменной только при отражении от полностью прозрачного диэлектрика. При наличии поглощения в материале фаза отраженного от него луча изменяется тем
больше, чем выше его показатель поглощения k. Крайним случаем являются металлы (k >> n), при отражении от которых фаза отраженного луча изменяется на p (180°). Таким образом, изменение фазы луча при отражении от поверхности материала, обозначаемое обычно термином «фазовый угол», является хотя и непрямой, но вполне однозначной характеристикой поглощения в материале. Поскольку k = k(w), то и фазовый угол является функцией частоты падающего излучения. При измерении энергетического коэффициента отражения R информация о значениях фазового угла (и соответственно о поглощении) теряется. Полную информацию об отраженном луче дает комплексный амплитудный коэффициент отражения:
где Зависимость комплексного амплитудного коэффициента отражения от угла падения j дается соответствующими уравнениями Френеля для перпендикулярно и параллельно поляризованных пучков:
и
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.222.102 (0.01 с.) |

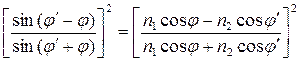 (2.2.1а)
(2.2.1а)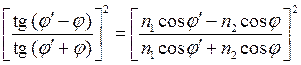 (2.2.1б)
(2.2.1б)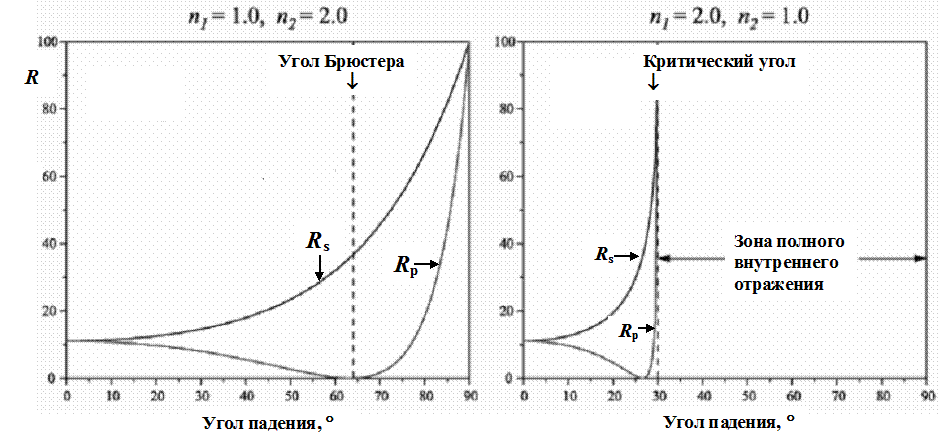
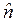 , что делает их достаточно сложными, В простейшем случае нормального падения из вакуума или воздуха соотношение (2.2.2б) принимает вид
, что делает их достаточно сложными, В простейшем случае нормального падения из вакуума или воздуха соотношение (2.2.2б) принимает вид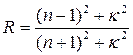 (2.2.3)
(2.2.3)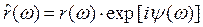 , (2.2.4)
, (2.2.4)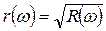 и y (w) - фазовый угол. Однако амплитудный коэффициент отражения не поддается прямому измерению, и поэтому для извлечения информации о значениях фазового угла из экспериментальных данных требуется достаточно сложная вычислительная процедура (см. ниже параграфы 3.2 и 6.1).
и y (w) - фазовый угол. Однако амплитудный коэффициент отражения не поддается прямому измерению, и поэтому для извлечения информации о значениях фазового угла из экспериментальных данных требуется достаточно сложная вычислительная процедура (см. ниже параграфы 3.2 и 6.1).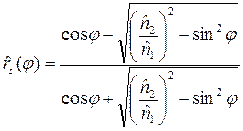 (2.2.5а)
(2.2.5а)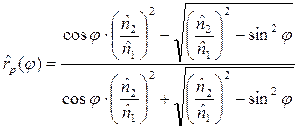 (2.2.5б)
(2.2.5б)


