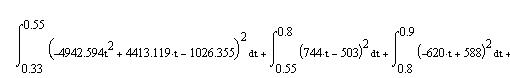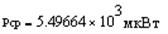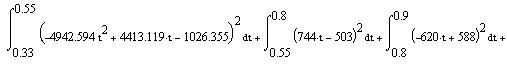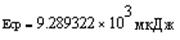Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование спектральных характеристик сигналаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Построение АЧХ и ФЧХ спектра периодического сигнала
Для анализа сигналов и их обработки важное значение имеет разложение заданной функции f(t) по различным ортогональным системам. Из теории математического анализа известно, что любую кусочно-непрерывную функцию S(t), суть детерминированный сигнал, для которой выполняется условие:
можно представить в виде суммы ортогональных функций: S(t)=C0φ0(t)+C1φ1(t)+…+Cnφn(t), где φ0(t), φ1(t),…,φn(t) - система ортогональных функций. Функции φn(t) называются ортогональными на отрезке (t1; t2), если эта совокупность удовлетворяет условию:
где i=1,2,3,4,…,m, k=1,2,3,4,…,m,
Коэффициенты Cn ряда определяются выражением:
Ряд, в котором коэффициенты Если система функций принимает комплексные значения, то приведенные выше определения обобщаются следующим образом: условие ортогональности- при квадрат нормы функции: коэффициенты обобщенного ряда Фурье: φ*(t) - есть функция комплексно сопряженная функции φ (t). Выбор наиболее рациональной ортогональной системы функций зависит от цели, преследуемой при разложении сложной функции в ряд. Так, например, для точного разложения сигнала на простейшие ортогональные функции наибольшее распространение получила система тригонометрических функций - синусов и косинусов. Это объясняется тем, что гармоническое колебание является единственной функцией времени, сохраняющей свою форму при прохождении через любую линейную цепь с постоянными параметрами, изменяются только амплитуда и фаза колебания. Итак, при разложении периодического сигнала S(t) в ряд Фурье по тригонометрическим функциям в качестве ортогональной системы берут I, cosω0t, sinω0t, cos2ω0t, sin2ω0t,…, cosnω0t, sinnω0t. Или в комплексной экспоненциальной форме: … Интервал ортогональности в этом случае совпадает с периодом функции S(t):
Тогда любую функцию S(t) на интервале (t;t +Т) можно представить рядом:
Коэффициенты
Амплитуда n-ой гармоники определяется выражением:
Фаза n-ой гармоники:
Распределение значений амплитуд по оси частот называется амплитудно-частотным спектром, а распределение фаз – фазочастотным спектром сигнала S (t). Рассчитаем амплитуду и фазу первых 25 гармоник периодического сигнала по следующим формулам: Коэффициент а(n) - Коэффициент b(n) - Амплитуда n-ой гармоники - Фаза n-ой гармоники - где n=0…25, T=1.69c,
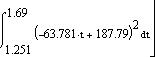
Произведем расчет первой гармоники, учитывая, что Т= 1,69 n=1.
Проверка:
Проверка:
Значения вычисленных 25 гармоник, соответствующих АЧХ, ФЧХ и частоты приведены в таблице 1. Таблица 1
Графики АЧХ и ФЧХ показаны на рисунках 3 и 4 соответственно.
Рисунок 3 – АЧХ периодического сигнала
Рисунок 4 – ФЧХ периодического сигнала
ИССЛЕДОВАНИЕ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
Построение АЧХ и ФЧХ спектра непериодического сигнала
Ряд Фурье справедлив для периодических сигналов. Спектр периодического сигнала дискретен. Если сигнал непериодический, то ряд Фурье применить нельзя. Однако, непериодический сигнал (одиночный) можно представить как периодический с периодом Т→∞ и продолжить рассмотрение непериодического сигнала на бесконечном интервале времени можно получить представление непериодического сигнала в виде спектральной плотности функции
Модуль и аргумент спектральной плотности определяются выражениями:
Первое из этих выражений можно рассматривать как АЧХ, а второе – как ФЧХ сплошного спектра непериодического сигнала s(t). На рисунках 6 и 7 представлено соответственно АЧХ и ФЧХ непериодического сигнала.
Рисунок 5 – АЧХ непериодического сигнала
Рисунок 6 – ФЧХ непериодического сигнала
Вывод: Модуль спектральной плотности одиночного импульса и огибающая линейчатого спектра периодического сигнала, полученного путём повторения заданного импульса, совпадают по форме и отличаются масштабом.
Средняя энергия и средняя мощность Периодического сигнала Пусть сигнал s(t) (ток, напряжение) представляет собой сложную периодическую функцию времени с периодом Т. Энергия такого сигнала, длящегося от t=-∞ до t=∞, бесконечно велика. Основной интерес представляет средняя мощность периодического сигнала и распределение этой мощности между отдельными гармониками сигнала. Очевидно, что средняя мощность сигнала, рассматриваемого на всей оси времени, совпадает с мощностью, средней за один период Т. Таким образом, средняя мощность периодического сигнала
При использовании тригонометрической формы ряда Фурье, учитывая, что С0=а0/2,
Если s(t) представляет собой ток i(t), то при прохождении его через сопротивление r выделяется мощность (средняя):
Символом I0=а0/2 обозначена постоянная составляющая, а In =An – амплитудой n-ой гармоники тока.
Итак, средняя мощность периодической последовательности равна сумме средних мощностей всех составляющих в спектре и не зависит от начальных фаз отдельных составляющих. Для данного сигнала средняя мощность равна:
Энергия периодического сигнала:
Проверка размерности величин:
Мы берём амплитуду в мВ, возводим в квадрат, получаем мкВ.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1082; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.170.253 (0.009 с.) |



 -есть норма функции.
-есть норма функции.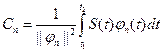
 определены выражением (4), называется обобщенным рядом Фурье по конкретной системе ортогональных функций φi(t).
определены выражением (4), называется обобщенным рядом Фурье по конкретной системе ортогональных функций φi(t).




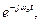 1,
1, 
 …
…

 ,
,  ,
, 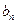 определяются с помощью выражения, пределы интегрирования задаются периодом Т:
определяются с помощью выражения, пределы интегрирования задаются периодом Т:

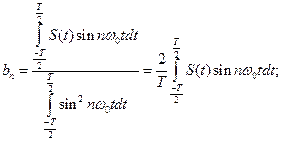






 =3.718 Гц
=3.718 Гц
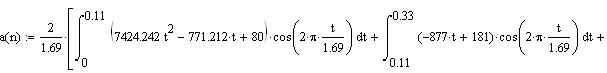











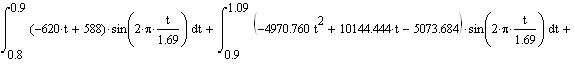











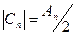 получаем
получаем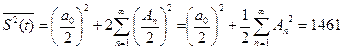 мВт
мВт