
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принципы оптимального приема сигналовСодержание книги Поиск на нашем сайте
Оптимальный приёмник Борьба с шумами и помехами при передаче сигнала по каналу связи была и будет одной из основных проблем радиотехники. Это относится к каналам, где передатчик и приемник информации разделены пространством (эфирные, спутниковые, кабельные каналы) или разделены во времени (каналы записи-воспроизведения на магнитном, проволочном, оптическом и твёрдотельном носителях). Проблема помехоустойчивости систем передачи информации решается путем специальной обработки сигнала, а также путем выбора специальных структур сигнала, использованием помехоустойчивого кодирования и модуляции. Принципы специальной обработки сигнала, т.е. метод оптимального приема сигнала, позволяет наилучшим образом выделить полезный сигнал на фоне помех. Задача ставится следующим образом. Пусть используется импульсный сигнал S (t), заранее известный, отличный от нуля на промежутке Приемник должен решить: в приходящем сигнале х (t) присутствует полезный сигнал S (t) или в нем содержится только сигнал помехи ξ (t). Составим скалярное произведение:
где φ (t) – весовая функция. Необходимо подобрать весовую функцию Величина b есть скалярное произведение функций В соответствии с неравенством Коши-Буняковского
которое записывается в виде:
Таким образом, величина полезного сигнала ограничена энергиями функций S (t) и φ (t) и достигает максимума, если Следовательно, в выражении (2.1) в качестве весовой функции φ (t), обеспечивающей наибольшее значение полезного сигнала b, необходимо взять сам сигнал S (t). В теории оптимального приёма доказывается, что эта же весовая функция обеспечивает наибольшее отношение сигнал/шум на выходе оптимального приёмника, если сигналом помехи будет белый шум, т.е. случайный сигнал, спектральная плотность мощности которого не зависит от частоты. На рис. 2.1 изображена блок-схема оптимального приемника. Здесь П – перемножитель, Г – генератор весовой функции, И – интегратор. Так как S (t) – импульсный сигнал, то в (2.1) интегрирование осуществляется в течение времени длительности импульса Этот сигнал поступает на один вход решающего устройства (Р), на второй вход которого подается опорный сигнал U OП. Величина U OП находится из условия минимума вероятности ошибки при принятии решения и определяется свойствами сигнала S (t) и статистическими параметрами случайного сигнала помехи ξ (t). Порядок расчета U OП здесь не рассматривается.
Рис. 2.1. Блок-схема оптимального приемника
Совокупность устройств, очерченных пунктиром на рис. 2.1, называют линейным фильтром, согласованным с сигналом, или коррелятором. Он может быть реализован так, как показано на рис. 2.1, и в этом случае его называют активным фильтром. Кроме того, он может быть реализован в виде фильтра в обычном понимании, к передаточной функции которого либо к его импульсной характеристике предъявлены специальные требования, о которых мы скажем ниже. В этом случае фильтр, согласованный с сигналом, называют пассивным фильтром. Название пришло из того времени, когда фильтры реализовывались только в базисе пассивных элементов.
Согласованный фильтр Пусть на вход фильтра поступает рассмотренный в предыдущем параграфе сигнал S (t). Сигнал на выходе фильтра
Зафиксируем момент времени t0 и выберем импульсную характеристику g (t) такой, чтобы в этот момент времени выходной сигнал U ВЫХ(t) принимал максимальное значение. Неравенство Коши-Буняковского применительно к (2.2) имеет вид:
При этом выходной сигнал U ВЫХ(t 0) в момент времени t 0 принимает максимальное значение при условии:
Заменой переменных t = t 0 - τ получаем требуемое значение импульсной характеристики согласованного фильтра:
В соответствии с (4.4) импульсная характеристика согласованного фильтра представляет собой с точностью до постоянной «зеркальную» копию входного сигнала S (t), сдвинутую на время t 0. На рис. 2.2 показано построение импульсной характеристики согласованного фильтра. Ясно, что момент времени t 0, при котором достигается максимум U ВЫХ(t), не может быть менее, чем длительность импульса Т. В противном случае импульсная характеристика g (t) будет отлична от нуля при t < 0, т.е. импульсный отклик на выходе фильтра появится раньше, чем на его вход поступит d - импульс.
Рис. 2.2. Иллюстрация к порядку построения импульсной характеристики
Запишем (24) в виде выражения
Интеграл в (2.5) представляет собой автокорреляционную функцию Окончательное выражение для сигнала на выходе согласованного фильтра имеет вид:
Таким образом, если в приёмнике используется оптимальный фильтр, согласованный с сигналом, то сигнал на его выходе представляет собой с точностью до постоянной автокорреляционную функцию входного сигнала, сдвинутую во времени на величину t 0. Обычно этот момент времени совпадает с моментом окончания импульсного сигнала, т.е. t 0 = T. Автокорреляционная функция, а, следовательно, сигнал на выходе оптимального фильтра, имеет несколько максимумов; наибольший из них B S(0), соответствующий моменту времени t 0 = T, равен энергии сигнала. В этот же момент времени выходной сигнал достигает максимума и происходит сравнение выходного сигнала с опорным сигналом. В цифровой системе передачи логической единице соответствует прямоугольный импульс сигнала положительной полярности, а логическому нулю – отрицательной полярности. В этих системах реализуется принцип поэлементного приёма сигналов. Это значит, что приёмник принимает решение отдельно по каждому элементу цифрового потока, т.е. по каждому прямоугольному импульсу положительной или отрицательной полярности. Определим функцию автокорреляции и вид сигнала на выходе оптимального приёмника, когда на его вход поступает прямоугольный импульс S(t) длительностью T:
Вычисление автокорреляционной функции иллюстрируется рис. 2.3.
Рис. 2.3 Иллюстрация к выводу формулы
Пусть первоначально
Так как функция автокорреляции чётная, то есть выполняется условие
Рис. 2.4 Функция автокорреляции
Сигналом на выходе является сдвинутая на время T функция автокорреляции:
График сигнала Uвых(t) на выходе оптимального приёмникапредставлен на рис.2.5.
Рис. 2.5 Сигнал на выходе оптимального приёмника
|
|||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

 и равный нулю вне этого промежутка. На вход приемника поступает сигнал
и равный нулю вне этого промежутка. На вход приемника поступает сигнал  , где
, где  - сигнал помехи.
- сигнал помехи. , (2.1)
, (2.1) таким образом, чтобы она максимизировала полезный сигнал
таким образом, чтобы она максимизировала полезный сигнал  .
. и φ (t), т.е.
и φ (t), т.е.  .
. выполняется неравенство:
выполняется неравенство:
 .
. . Этот факт очевиден, так как с геометрической точки зрения скалярное произведение двух векторов пропорционально проекции одного вектора на другой. Проекция будет наибольшей, если векторы совпадают по направлению.
. Этот факт очевиден, так как с геометрической точки зрения скалярное произведение двух векторов пропорционально проекции одного вектора на другой. Проекция будет наибольшей, если векторы совпадают по направлению. , по окончании которого на выходе интегратора появляется не зависящий от времени сигнал y.
, по окончании которого на выходе интегратора появляется не зависящий от времени сигнал y.
 определяется интегралом Дюамеля, т.е. является сверткой функции S (t) и импульсного отклика g (t).
определяется интегралом Дюамеля, т.е. является сверткой функции S (t) и импульсного отклика g (t).  . (2.2)
. (2.2) . (2.3)
. (2.3)
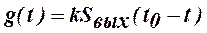 (2.4)
(2.4)
 и подставим его в (2.2):
и подставим его в (2.2): . (2.5)
. (2.5)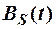 сигнала S (t), сдвинутую во времени на величину t 0.
сигнала S (t), сдвинутую во времени на величину t 0. . (2.6)
. (2.6)

 . Проведём преобразования:
. Проведём преобразования: .
. , то для всех значений τ функция автокорреляции имеет вид, представленный на рис. 2.4:
, то для всех значений τ функция автокорреляции имеет вид, представленный на рис. 2.4:







