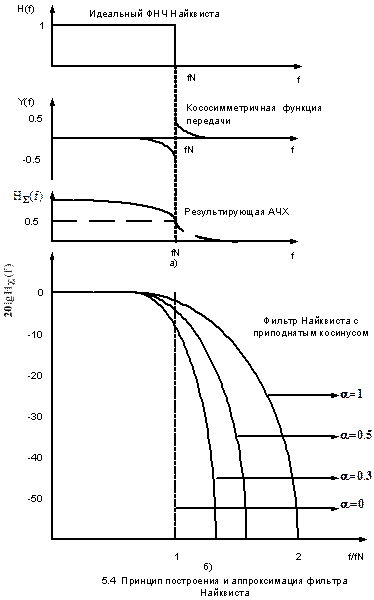Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стандарт ГОСТ Р52023 – 2003. Сети распределительные систем кабельного телевиденияСодержание книги
Поиск на нашем сайте
Введение Цифровая форма представления сигнала давно уже перестала быть объектом для обсуждений и споров. Эта форма используется практически на всех этапах создания, консервации и транспортирования телевизионного сигнала. Система телевизионного вещания предназначена для доставки телевизионных программ от источника программ к абоненту. Она включает в себя студийное оборудование, оборудование канала передачи и абонентские устройства. Студийное оборудование осуществляет преобразование, обработку, консервацию и кодирование аудио и видеоинформации. Так как это оборудование является источником программ, то именно в нём было впервые использовано цифровое представление сигнала. Первоначально цифровое студийное оборудование участвовало только во внутреннем цикле создания в студии телевизионной программы. Оно обеспечивало широкие возможности работы с аудио и видеоматериалом, недоступные аналоговым методам. Однако сигналы, выходящие со студии для подачи в систему телевизионного вещания были аналоговыми, так как сама система вещания оставалась аналоговой. Телевизионный сигнал в цифровой форме имеет спектр частот в десятки раз шире, чем аналоговый. Поэтому реальный переход к цифровому телевизионному вещанию оказался возможным только после разработки методов цифрового сжатия (компрессирования) видео и аудиосигналов в соответствии со стандартами MPEG2 [1], MPEG4 [2]. Эти стандарты предусматривает организацию элементарных программных потоков (ПП), соответствующих одной телевизионной программе и мультиплексирование нескольких ПП в единый транспортный поток (ТП). Таким образом, входным сигналом в системе цифрового телевизионного вещания (ЦТВ) является стандартизованный транспортный поток в форматах MPEG2, MPEG4 который поступает в эфирный, спутниковый или кабельный канал передачи. Несмотря на использование компрессии ширина спектра ТП значительно шире полосы частот, выделяемой в системе ЦТВ для его передачи. Поэтому в канале передачи предусматривается многоуровневая модуляция сигнала несущей радиочастоты цифровым сигналом, которая обеспечивает согласование ширины спектра цифрового сигнала ТП с шириной канала передачи. Организация системы ЦТВ, т.е. состав и правила выполнения операций над сигналом ТП определяется стандартами DVB (Digital Video Broadcasting) и, в частности, DVB – T для эфирного вещания [2], DVB – S для спутникового вещания [3], DVB – C для кабельного вещания [4,5]. Совершенно ясно, что введение в эксплуатацию ЦТВ имеет явные преимущества для компаний, предоставляющих услуги телевизионного вещания. Это обусловлено, в частности, тем, что на одной несущей частоте может быть передано сразу несколько ТВ программ, что значительно снижает затраты на организацию вещания. Качество видео и аудиосигналов, доставляемых абоненту в системе ЦТВ, выше, чем для аналоговых систем вещания. Однако простое улучшение качества телевизионного изображения по сравнению с достаточно высоким качеством для современных аналоговых систем ТВ вещания вряд ли является привлекательным стимулом для абонентов. Только предоставление дополнительных услуг может обеспечить рентабельность ЦТВ. Именно поэтому стандарт предусматривает построение интерактивной сети ЦКТВ, предоставляющей абонентам возможность подключения к скоростному INTERNET, пользование услугами электронной почты, возможность проведения игр между абонентами, банковские услуги на дому и т.д. И всё это происходит на фоне получения абонентами полного набора ТВ программ. Стандарт ETSI ES 200 800 [4] описывает структуру передающего и абонентского оборудования и операции над сигналами, предусмотренные при организации вещательного канала. Стандарт ETSI EN 300 429 [5] описывает структуру передающего и абонентского оборудования и операции над сигналами, предусмотренные при организации интерактивного канала. В России построение сетей кабельного телевидения регламентируется стандартом ГОСТ Р52023 – 2003, в котором установлены параметры сетей и методы их измерений. Стандарт распространяется как на системы аналогового, так и цифрового кабельного телевидения.
Стандарт ГОСТ Р52023 – 2003. Сети распределительные систем кабельного телевидения Область применения Рассматриваемый стандарт [1] распространяется на распределительные сети систем кабельного телевидения с частотным разделением каналов и полосой частот от 5 до 1000 МГц, предназначенные для двунаправленной или однонаправленной передачи радиосигналов телевидения, радиовещания и других сигналов электросвязи. Полоса частот от 40 до 1000 МГц предназначена для распределения радиосигналов в прямом направлении, полоса частот от 5 до 30 МГц – для передачи радиосигналов в обратном направлении. Допускается расширение полосы частот обратного направления за счет полосы частот прямого направления. Стандарт устанавливает параметры, технические требования, методы измерений и испытаний кабельных распределительных сетей при проектировании, строительстве, сертификации и эксплуатации.
Принципы оптимального приема сигналов Оптимальный приёмник Борьба с шумами и помехами при передаче сигнала по каналу связи была и будет одной из основных проблем радиотехники. Это относится к каналам, где передатчик и приемник информации разделены пространством (эфирные, спутниковые, кабельные каналы) или разделены во времени (каналы записи-воспроизведения на магнитном, проволочном, оптическом и твёрдотельном носителях). Проблема помехоустойчивости систем передачи информации решается путем специальной обработки сигнала, а также путем выбора специальных структур сигнала, использованием помехоустойчивого кодирования и модуляции. Принципы специальной обработки сигнала, т.е. метод оптимального приема сигнала, позволяет наилучшим образом выделить полезный сигнал на фоне помех. Задача ставится следующим образом. Пусть используется импульсный сигнал S (t), заранее известный, отличный от нуля на промежутке Приемник должен решить: в приходящем сигнале х (t) присутствует полезный сигнал S (t) или в нем содержится только сигнал помехи ξ (t). Составим скалярное произведение:
где φ (t) – весовая функция. Необходимо подобрать весовую функцию Величина b есть скалярное произведение функций В соответствии с неравенством Коши-Буняковского
которое записывается в виде:
Таким образом, величина полезного сигнала ограничена энергиями функций S (t) и φ (t) и достигает максимума, если Следовательно, в выражении (2.1) в качестве весовой функции φ (t), обеспечивающей наибольшее значение полезного сигнала b, необходимо взять сам сигнал S (t). В теории оптимального приёма доказывается, что эта же весовая функция обеспечивает наибольшее отношение сигнал/шум на выходе оптимального приёмника, если сигналом помехи будет белый шум, т.е. случайный сигнал, спектральная плотность мощности которого не зависит от частоты. На рис. 2.1 изображена блок-схема оптимального приемника. Здесь П – перемножитель, Г – генератор весовой функции, И – интегратор. Так как S (t) – импульсный сигнал, то в (2.1) интегрирование осуществляется в течение времени длительности импульса Этот сигнал поступает на один вход решающего устройства (Р), на второй вход которого подается опорный сигнал U OП. Величина U OП находится из условия минимума вероятности ошибки при принятии решения и определяется свойствами сигнала S (t) и статистическими параметрами случайного сигнала помехи ξ (t). Порядок расчета U OП здесь не рассматривается.
Рис. 2.1. Блок-схема оптимального приемника
Совокупность устройств, очерченных пунктиром на рис. 2.1, называют линейным фильтром, согласованным с сигналом, или коррелятором. Он может быть реализован так, как показано на рис. 2.1, и в этом случае его называют активным фильтром. Кроме того, он может быть реализован в виде фильтра в обычном понимании, к передаточной функции которого либо к его импульсной характеристике предъявлены специальные требования, о которых мы скажем ниже. В этом случае фильтр, согласованный с сигналом, называют пассивным фильтром. Название пришло из того времени, когда фильтры реализовывались только в базисе пассивных элементов.
Согласованный фильтр Пусть на вход фильтра поступает рассмотренный в предыдущем параграфе сигнал S (t). Сигнал на выходе фильтра
Зафиксируем момент времени t0 и выберем импульсную характеристику g (t) такой, чтобы в этот момент времени выходной сигнал U ВЫХ(t) принимал максимальное значение. Неравенство Коши-Буняковского применительно к (2.2) имеет вид:
При этом выходной сигнал U ВЫХ(t 0) в момент времени t 0 принимает максимальное значение при условии:
Заменой переменных t = t 0 - τ получаем требуемое значение импульсной характеристики согласованного фильтра:
В соответствии с (4.4) импульсная характеристика согласованного фильтра представляет собой с точностью до постоянной «зеркальную» копию входного сигнала S (t), сдвинутую на время t 0. На рис. 2.2 показано построение импульсной характеристики согласованного фильтра. Ясно, что момент времени t 0, при котором достигается максимум U ВЫХ(t), не может быть менее, чем длительность импульса Т. В противном случае импульсная характеристика g (t) будет отлична от нуля при t < 0, т.е. импульсный отклик на выходе фильтра появится раньше, чем на его вход поступит d - импульс.
Рис. 2.2. Иллюстрация к порядку построения импульсной характеристики
Запишем (24) в виде выражения
Интеграл в (2.5) представляет собой автокорреляционную функцию Окончательное выражение для сигнала на выходе согласованного фильтра имеет вид:
Таким образом, если в приёмнике используется оптимальный фильтр, согласованный с сигналом, то сигнал на его выходе представляет собой с точностью до постоянной автокорреляционную функцию входного сигнала, сдвинутую во времени на величину t 0. Обычно этот момент времени совпадает с моментом окончания импульсного сигнала, т.е. t 0 = T. Автокорреляционная функция, а, следовательно, сигнал на выходе оптимального фильтра, имеет несколько максимумов; наибольший из них B S(0), соответствующий моменту времени t 0 = T, равен энергии сигнала. В этот же момент времени выходной сигнал достигает максимума и происходит сравнение выходного сигнала с опорным сигналом. В цифровой системе передачи логической единице соответствует прямоугольный импульс сигнала положительной полярности, а логическому нулю – отрицательной полярности. В этих системах реализуется принцип поэлементного приёма сигналов. Это значит, что приёмник принимает решение отдельно по каждому элементу цифрового потока, т.е. по каждому прямоугольному импульсу положительной или отрицательной полярности. Определим функцию автокорреляции и вид сигнала на выходе оптимального приёмника, когда на его вход поступает прямоугольный импульс S(t) длительностью T:
Вычисление автокорреляционной функции иллюстрируется рис. 2.3.
Рис. 2.3 Иллюстрация к выводу формулы
Пусть первоначально
Так как функция автокорреляции чётная, то есть выполняется условие
Рис. 2.4 Функция автокорреляции
Сигналом на выходе является сдвинутая на время T функция автокорреляции:
График сигнала Uвых(t) на выходе оптимального приёмникапредставлен на рис.2.5.
Рис. 2.5 Сигнал на выходе оптимального приёмника Поле сигналов Для передачи информационного сигнала по каналу используется синусоидальный сигнал U (t) = A sin(2π f Н t + φ), параметрами которого являются амплитуда A, несущая частота f Н, и фазовый угол φ. Если зафиксировать m вариантов сочетаний параметров A r, φ r, r =1,… m, то получим m различных сигналов U r(t) = A rsin(2π f Н t + φr). Разделим цифровой поток на фрагменты из n последовательно расположенных элементов. Число таких фрагментов, отличающихся друг от друга, равно m=2n. Каждому фрагменту, который называется кортежем, поставим в соответствие один из m различных сигналов U r(t). Таким образом, реализуется процесс m уровневой модуляции сигнала несущей частоты сигналом цифрового потока. Получить m вариантов сочетания параметров A r, φ r, r =1,… m можно множеством способов. Один из вариантов, т.е. один из методов модуляции, является наиболее помехоустойчивым и называется квадратурно-амплитудным методом КAM m [6]. В общем случае, следуя теории многоуровневой модуляции [6], можно рассмотреть плоскость, на которой расположено множество точек, каждая из которых соответствует n -значному двоичному числу, n =ln m / ln2, где m – число уровней модуляции. Каждой r -ой точке из множества, Этот сигнал генерируется в передатчике и, пройдя через среду распространения, поступает на вход приемника. Таким образом, налицо пространство сигналов, которое будем рассматривать как двумерное функциональное гильбертово пространство. Выделим в этом пространстве ортонормированный базис
Скалярное произведение в гильбертовом пространстве определяется в виде:
Подставим (3.2), (3.3) в (3.1):
Выражение (3.4) представляет собой запись операций над сигналами, которые производятся в передающих устройствах транспортирования многоуровневого сигнала. Эти устройства построены по принципу квадратурной обработки, т.е. имеют два квадратурных канала в соответствии со структурой устройства, представленной на рисунке 3.5. На вход 1 поступает n -значное двоичное число, на выходе 2 – сигнал U r sin (ωн t + φr).
Рис. 3.5. Структура передающего устройства (1 – Вход, 2 – Выход)
Из (3.4) следует, что сигнал Такое представление сигналов, называемое полем сигналов (constellation), изображено на рис.6.4 для частного случая многоуровневой модуляции – квадратурно-амплитудной модуляции КАМ 64.
Основные понятия о помехоустойчивом кодировании На вход головной станции кабельного телевидения поступает цифровой сигнал, который представляет собой транспортный поток (ТП) в виде следующих друг за другом транспортных пакетов длиной 188 байт. В результате прохождения информационного сигнала по каналу передачи в принятом сигнале под влиянием помех возникают ошибки. Для их обнаружения и исправления используется процедура помехоустойчивого кодирования с помощью корректирующих кодов. Обычно количество исправленных ошибок меньше, чем обнаруженных. Исправляющей способностью кода называется количество ошибок в транспортном пакете, которые код может исправить. Идея построения корректирующих кодов состоит во введении p дополнительных символов в транспортный пакет, содержащий k информационных двоичных символов. Общее число двоичных символов становится равным n= k+p. Доля информационных символов, т.е. R= k/n= k/(p+k) называется относительной скоростью кода. Сам код обозначается в виде (n,k). Он имеет 2 nвозможных кодовых комбинаций. Из них 2 k– число разрешённых кодовых комбинаций, а кодовые комбинации числом (2n– 2k) являются запрещёнными. В передаваемом транспортном потоке присутствуют только разрешённые кодовые комбинации, которые должны обладать следующим свойством – при появлении ошибки, т.е. при изменении любого двоичного символа, разрешённая кодовая комбинация переходит в запрещённую, что легко обнаруживается и свидетельствует о наличии ошибки. Если это требование к коду не выполняется, то разрешённая кодовая комбинация в результате ошибки переходит в другую разрешённую и обнаружить ошибку невозможно. Самым первым примером помехоустойчивого кодирования, реализованным в системах передачи телеграфных сообщений, является «проверка на чётность». Суть его состоит в том, что в каждую кодовую комбинацию добавляется двоичный символ, который называется контрольным или поверочным битом. Этому биту присваивается значение 1, если количество единиц в кодовой комбинации является нечётным числом и значение 0 в противном случае. Таким образом общее количество бит в передаваемой кодовой комбинации с учётом поверочного бита является чётным. Если в принятой кодовой комбинации общее количество бит окажется нечётным числом, то это значит, что произошла ошибка и она обнаружена. Таким образом, проверка на чётность позволяет обнаружить одиночные ошибки, но не позволяет их исправить. В теории помехоустойчивого кодирования для оценки работоспособности кода вводится понятие кодового расстояния или расстояния Хэмминга dмежду двумя кодовыми комбинациями Если расстояние Хэмминга между любыми разрешёнными кодовыми комбинациями равно единице, т.е. d= 1, то при появлении ошибки одна разрешённая кодовая комбинация превратится в другую разрешённую и ошибка не будет обнаружена. Следовательно, для обнаружения одной одиночной ошибки необходимо выбрать такие разрешённые кодовые комбинации, что бы расстояние Хэмминга между ними было бы не менее двух, т.е. d≥ 2. Для обнаружения l одиночных ошибок должно выполняться требование d≥ l + 1. Для исправления одиночных ошибок требуется, что бы расстояние Хэмминга между двумя любыми разрешёнными кодовыми комбинациями было бы не менее трёх. В этом случае принятая и ставшая запрещённой в результате ошибки кодовая комбинация заменяется ближайшей по Хэммингу из разрешённых кодовых комбинаций. При единичной ошибке принятая запрещённая кодовая комбинация отличается от переданной разрешённой на одну единицу, а от остальных на две единицы. По этому признаку ошибка исправляется. Для коррекции, т.е. для исправления нескольких r2ошибок, расстояние между любыми двумя разрешёнными кодовыми комбинациями должно удовлетворять условию d≥ 2* r2+1. Для исправления пакетных, т.е. расположенных рядом ошибок, разработан ряд корректирующих кодов и, в частности, код БЧХ (Bose, Chaudhuri, Hockwinham) и вытекающий из него код Рида – Соломона. Последний используется в Европейском стандарте DVBи имеет 188 информационных байта в пакете транспортного потока и 16 поверочных символов. Таким образом пакет транспортного потока содержит 204 байта. Фильтр Найквиста Рассмотрим модель идеального канала передачи с прямоугольной амплитудно-частотной (АЧХ)
Частота среза АЧХ f N = 1/2 T = f T /2 называется частотой Найквиста, где f T =1/ T – частота следования прямоугольных видеоимпульсов. Пусть на вход идеального канала подаётся последовательность δ импульсов. Тогда сигнал на выходе будет представлять собой последовательность его импульсных характеристик
Характерной особенностью его импульсных характеристик является то, что в момент времени, когда одна импульсная характеристика достигает своего максимума, значения остальных импульсных характеристик равны нулю. При подаче на вход идеального канала прямоугольных видеоимпульсов эта особенность сохраняется, если в канал ввести специализированный корректор АЧХ [2]. Как показано в разделе 2, оптимальный приёмник принимает решение в моменты времени, когда автокорреляционная функция входного прямоугольного видеоимпульса, т.е. выходной сигнал, принимает наибольшее значение в момент окончания видеоимпульса. Таким образом, в идеальном канале с прямоугольной АЧХ и линейной ФЧХ реализуются функции оптимального приёмника без межсимвольных искажений, так как в момент принятия решения на его выходе присутствует сигнал только одного видеоимпульса, а сигналы от остальных предыдущих видеоимпульсов равны нулю. Однако предложенный Найквистом идеальный канал физически не реализуем. Для решения этой задачи Найквист сформулировал и доказал принцип частичной симметрии, проиллюстрированный рисунком 5.4,а. В соответствии с этим принципом, если просуммировать АЧХ идеального фильтра Найквиста H (f) с кососимметричной функцией передачи H (f), то суммарная функция H Σ(f) физически реализуема в виде фильтра нижних частот и обеспечивает отсутствие межсимвольных искажений. На практике функция H Σ(f) аппроксимируется функцией приподнятого косинуса:
где α = f Х/ f N – коэффициент скругления. φ (f) =φ0 - k*f - линейная фазочастотная характеристика.
Малые значения коэффициента α обеспечивают малое значение коэффициента передачи H Σ(f), близкое к нулю на частотах выше частоты Найквиста. Однако, при этом возникает большая неравномерность коэффициента передачи H Σ(f) в полосе пропускания. Большие значения коэффициента α обеспечивают требования в полосе пропускания и плохо удовлетворяют требованиям в полосе задерживания. Реально используемые значения коэффициента α лежат в пределах от 0,15 до 0,3.
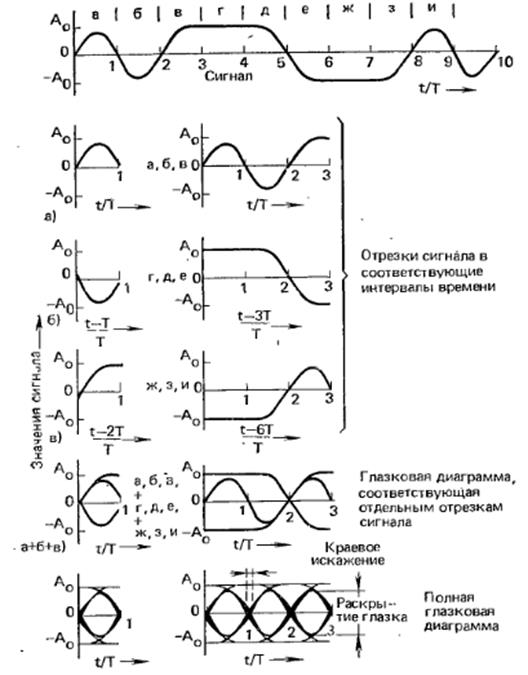
Глазковая диаграмма В разделе 5.1 показано, что при ограниченной полосе пропускания канала возникают межсимвольные искажения. Их наличие, а также присутствие шумов в канале приводит к возникновению ошибок в принятом сигнале. Для визуального контроля степени искажения и зашумленности сигнала используется глазковая диаграмма (глаз-диаграмма, Eye), которая в реальном масштабе времени отображается на экране осциллографа. Глаздиаграмма используется для визуального текущего контроля состояния тракта передачи и приёма цифровых сигналов. Для получения глаз-диаграммы на вход осциллографа с выхода приёмника подаётся поток символов, при этом период строчной развёртки должен быть кратным периоду следования символов. В этом случае текущая последовательность символов будет наложена на предыдущие. За счёт инерционности зрения изображение, видимое на экране, представляет собой глаз-диаграмму, процесс образования которой иллюстрируется рис. 5.5. По вертикали глаз-диаграммы можно непосредственно определить сумму отклонения сигнала от порогового уровня в моменты отсчёта, т.е. в моменты принятия решения о переданном символе. Эта величина называется раскрытием «глаза». По горизонтальному раскрытию «глаза» можно оценить межсимвольные (краевые) искажения.
Рис. 5.5. Глаз-диаграмма
Глаз-диаграмма является одной из важнейших характеристик передатчиков. На основе анализа глаз-диаграммы можно делать выводы о качестве передатчика, рассчитывать параметры линии, прогнозировать стабильность и качество передачи данных. Глаз-диаграмма имеет большое значение при оценке качества трансиверов, которые используются в телекоммуникационном оборудовании. Важность ее анализа растет со скоростью передачи данных. Наиболее простой пример – диаграмма для троичного (возможные уровни -1, 0, +1) линейного сигнала при косинус-квадратной форме входного сигнала регенератора (рис. 5.6.). Хорошо видна область («раскрыв») глаз-диаграммы, в пределах которой должна производиться операция опознания сигнала для каждого из двух уровней решения. Горизонтальные линии, обозначенные как -1, 0 и +1, соответствуют амплитудам импульсов при отсутствии помех, а вертикальные линии через каждый тактовый интервал Т – идеальным моментам решения.
Рис.5.6. Глаз-диаграмма идеального троичного сигнала.
Процесс принятия решения показан в виде двух крестиков в каждом «раскрыве» глаз-диаграммы. Вертикальная черта каждого крестика определяет момент решения, а горизонтальная – его уровень. Гарантией безошибочной регенерации цифрового сигнала является наличие вблизи каждого крестика определенной области, в пределах которой и должно происходить опознание сигнала. Наличие помех приводит к сокращению этой области по сравнению с идеальным случаем. Минимальное расстояние между центром крестиков и краями «глаза» служит мерой запаса помехозащищенности. Запас уменьшается как из-за искажений формы импульса, так и вследствие несовершенства самого процесса принятия решения. Первая причина приводит к уменьшению «раскрыва» глаз-диаграммы, а вторая – к перемещению точки принятия решения вдоль границ глаза. Возникающие вследствие двух указанных причин искажения принято подразделять на амплитудные и временные, соответствующие смещению точки принятия решения по вертикали и горизонтали. Для удобства дальнейших рассуждений будем считать, что точка принятия решения остается неподвижной, а уменьшается «раскрыв». Степень уменьшения «раскрыва» глаз-диаграммы по вертикали определяется результирующими искажениями, вызванными межсимвольными помехами, эхосигналами, изменениями амплитуды импульсов на выходе регенератора, погрешностями порогов решающих устройств. В результате воздействий появляется вертикальная составляющая искажений глаз-диаграммы ΔA. Именно на эту величину должны быть сдвинуты края идеальной глаз-диаграммы (рис. 5.7.).
Рис. 5.7. Глаз-диаграмма троичного сигнала при наличии помех.
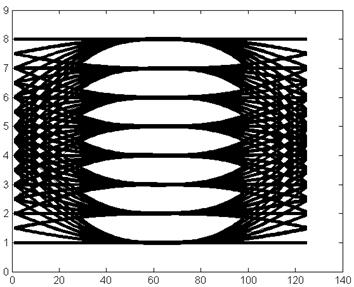
Временные искажения глаз-диаграммы ΔТ, включающие несоответствие моментов решения их статическим значениям и джиттер, учитываются обычно в смещении границ «глаза» по горизонтали. Очевидно, что для компенсации ухудшения реальной глаз-диаграммы по сравнению с идеальной необходимо увеличить величину отношения сигнал/шум на величину ΔS/N = 20 lg (H/h), дБ. Здесь H и h представляют собой вертикальный «раскрыв» идеальной и реальной глаз-диаграмм, соответственно. На рис.5.8 представлены графики пяти символов на входе фильтра Найквиста и на его выходе. На рис. 5.9, рис. 5.10 приведены изображения глаз-диаграмм одного символа, для отношения сигнал /шум, соответственно, 35 дБ и 50 дБ. Изображения наглядно демонстрируют увеличение «раскрыва» глаз – диаграммы при увеличении отношения сигнал/шум.
Рис. 5.8. Изображения символов на входе и на выходе фильтра Найквиста
Рис. 5.9. Изображение глаз-диаграммы одного символа, отношение сигнал /шум 35 дБ
Рис. 5.10. Изображение глаз-диаграммы одного символа, отношение сигнал /шум 50 дБ
Принцип модуляции СOFDM Рассмотренные в разделе 5 межсимвольные искажения имеют своей причиной рассогласование между шириной спектра цифрового потока и шириной диапазона частот, занимаемого каналом передачи. При этом предполагается, что существует только один канал передачи между передатчиком и приёмником. Между тем радиосигнал, распространяемый в условиях многоэтажной городской застройки и попадающий в приёмник, представляет собой сумму прямого и отражённых от зданий сигналов, задержанных относительно прямого сигнала. Налицо многолучевое распространение радиосигналов и, как следствие, их суперпозиция (интерференция). Это же явление возникает при приёме радиосигнала в движущемся автомобиле. Следствием многолучевой интерференции является искажение принимаемого сигнала в виде периодического замирания его уровня. В цифровых системах передачи и, в частности в системах цифрового эфирного телевидения, в беспроводных сетях передачи данных WiMAX, и в системах цифрового спутникового телевидения используется современный метод передачи цифрового сигнала по радиоканалу. Этот метод получил название - ортогональное частотное мультиплексирование OFDM(OrthogonalFrequencyDivisionMultiplex). Метод основан на распределении передаваемого цифрового потока по множеству частотных подканалов с одновременной параллельной передачей радиосигналов на всех этих подканалах. Рис. 6.1 поясняет принцип метода.
Рис. 6.1 Принцип построения суммарного сигнала
Цифровой поток, представляющий случайную последовательность единиц и нулей делится на Nподпотоков. Генерируются Nнесущих гармонических сигналов, частоты которых fi i= 0, …, N-1 находятся на равных расстояниях друг от друга и отличаются на величину Δf. Каждый из выделенных подпотоков модулирует один сигнал несущей частоты. На рис. 6.2 изображён суммарный сигнал. Суммарная ширина спектра частот модулированного колебания равна: Δfк= Δf*N.
Рис. 6.2 Суммарный сигнал
Введение Цифровая форма представления сигнала давно уже перестала быть объектом для обсуждений и споров. Эта форма используется практически на всех этапах создания, консервации и транспортирования телевизионного сигнала. Система телевизионного вещания предназначена для доставки телевизионных программ от источника программ к абоненту. Она включает в себя студийное оборудование, оборудование канала передачи и абонентские устройства. Студийное оборудование осуществляет преобразование, обработку, консервацию и кодирование аудио и видеоинформации. Так как это оборудование является источником программ, то именно в нём было впервые использовано цифровое представление сигнала. Первоначально цифровое студийное оборудование участвовало только во внутреннем цикле создания в студии телевизионной программы. Оно обеспечивало широкие возможности работы с аудио и видеоматериалом, недоступные аналоговым методам. Однако сигналы, выходящие со студии для подачи в систему телевизионного вещания были аналоговыми, так как сама система вещания оставалась аналоговой. Телевизионный сигнал в цифровой форме имеет спектр частот в десятки раз шире, чем аналоговый. Поэтому реальный переход к цифровому телевизионному вещанию оказался возможным только после разработки методов цифрового сжатия (компрессирования) видео и аудиосигналов в соответствии со стандартами MPEG2 [1], MPEG4 [2]. Эти стандарты предусматривает организацию элементарных программных потоков (ПП), соответствующих одной телевизионной программе и мультиплексирование нескольких ПП в единый транспортный поток (ТП
|
|||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.126.51 (0.028 с.) |

 и равный нулю вне этого промежутка. На вход приемника поступает сигнал
и равный нулю вне этого промежутка. На вход приемника поступает сигнал  , где
, где  - сигнал помехи.
- сигнал помехи. , (2.1)
, (2.1) таким образом, чтобы она максимизировала полезный сигнал
таким образом, чтобы она максимизировала полезный сигнал  .
. и φ (t), т.е.
и φ (t), т.е.  .
. выполняется неравенство:
выполняется неравенство:
 .
. . Этот факт очевиден, так как с геометрической точки зрения скалярное произведение двух векторов пропорционально проекции одного вектора на другой. Проекция будет наибольшей, если векторы совпадают по направлению.
. Этот факт очевиден, так как с геометрической точки зрения скалярное произведение двух векторов пропорционально проекции одного вектора на другой. Проекция будет наибольшей, если векторы совпадают по направлению. , по окончании которого на выходе интегратора появляется не зависящий от времени сигнал y.
, по окончании которого на выходе интегратора появляется не зависящий от времени сигнал y.
 определяется интегралом Дюамеля, т.е. является сверткой функции S (t) и импульсного отклика g (t).
определяется интегралом Дюамеля, т.е. является сверткой функции S (t) и импульсного отклика g (t).  . (2.2)
. (2.2) . (2.3)
. (2.3)
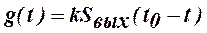 (2.4)
(2.4)
 и подставим его в (2.2):
и подставим его в (2.2): . (2.5)
. (2.5)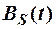 сигнала S (t), сдвинутую во времени на величину t 0.
сигнала S (t), сдвинутую во времени на величину t 0. . (2.6)
. (2.6)

 . Проведём преобразования:
. Проведём преобразования: .
. , то для всех значений τ функция автокорреляции имеет вид, представленный на рис. 2.4:
, то для всех значений τ функция автокорреляции имеет вид, представленный на рис. 2.4:




 ставится в соответствие сигнал
ставится в соответствие сигнал 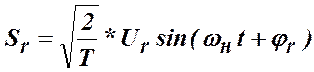 , являющиёся гармоническим колебанием с частотой несущей
, являющиёся гармоническим колебанием с частотой несущей  , амплитудой
, амплитудой  и начальной фазой φr
и начальной фазой φr и запишем сигнал Sr в этом базисе:
и запишем сигнал Sr в этом базисе: (3.1)
(3.1) (3.2)
(3.2) (3.3)
(3.3) (3.4)
(3.4)
 можно рассматривать, как вектор в евклидовом пространстве с осями I и Q, координаты которого задаются синфазной составляющей
можно рассматривать, как вектор в евклидовом пространстве с осями I и Q, координаты которого задаются синфазной составляющей  (ось I) и квадратурной составляющей
(ось I) и квадратурной составляющей  (ось Q).
(ось Q). Оно определяется как число двоичных разрядов, в которых эти комбинации различаются. Расстояние Хэмминга между двумя взятыми для примера кодовыми комбинациями x= {110101}, y= {100100} равно d= 2.
Оно определяется как число двоичных разрядов, в которых эти комбинации различаются. Расстояние Хэмминга между двумя взятыми для примера кодовыми комбинациями x= {110101}, y= {100100} равно d= 2.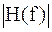 и линейной фазо-частотной (ФЧХ) φ (f) характеристиками, представленными на рис. 5.2.
и линейной фазо-частотной (ФЧХ) φ (f) характеристиками, представленными на рис. 5.2.
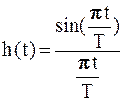 , представленных на рис. 5.3.
, представленных на рис. 5.3.
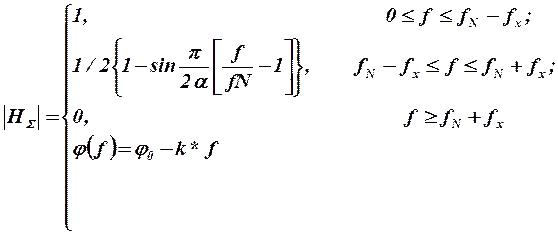 ,
,