
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение частоты сигнала и сдвига фаз методом фигур Лиссажу.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При подаче на пластины " Y " и " Х " осциллографа гармонических сигналов на экране получаются кривые различной формы, получившие название фигур Лиссажу. Форма фигур и их ориентация относительно осей определяется соотношением частот и сдвигом фаз между сигналами, подаваемыми на различные пластины осциллографа. Осциллограф С1-83 двухлучевой, что дает возможность пронаблюдать как временную развертку складываемых сигналов, так и результат сложения.
Подбирая частоту звукового генератора, пронаблюдать и проанализировать вид фигур, получающихся при соотношении частот 1:1, 1:2, 2:1, 3:1 и т.д., определить частоту сигнала, снимаемого с ВС-24. клонный эллипс, по углу наклона которого можно судить о величине сдвига фаз (Рис. 9). Он определяется по формулам:
где X 0, Y 0 – проекции эллипса на оси координат, а x 0, y 0 – отрезки между точками пересечения эллипса с осями координат. Определить сдвиг фаз между колебаниями напряжения на резисторе и реактивном сопротивлении (конденсаторе или катушке индуктивности) можно и другим способом, используя двухлучевой осциллограф (Рис. 10). В этом случае включается временная развертка на оба входа " Y 1" и " Y 2", на которые подаются сигналы с резистора и с конденсатора (или катушки), и по смещению одной синусоиды относительно другой определяется сдвиг фаз одного сигнала относительно другого:
причем знак сдвига фаз определяется по тому, опережает или отстает синусоида UC или (UL)относительно UR. Вопросы к зачету по работе. – Из каких блоков состоит электронно-лучевой осциллограф? – Назначение и принцип действия основных блоков осциллографа. – Для чего предназначен электронно-лучевой осциллограф? – Электрические схемы для снятия вольт-вольтовых и временных характеристик. – Каким образом производить численные измерения с использованием электронно-лучевого осциллографа?
Лабораторная работа № 9 Изучение закономерностей электромагнитных колебаний Цель работы. Изучить закономерности колебаний в электромагнитном колебательном контуре на примере затухающих колебаний. Знания, необходимые для допуска к работе. – Энергия электрического и магнитного полей; – Свободные, затухающие, вынужденные колебания; – Электрический колебательный контур, его рабочие параметры. Краткие сведения из теории.
Допустим, что при разомкнутом ключе конденсатор зарядили до напряжения U 0 (сообщили заряд Q 0). Энергия электрического поля равна:  . .
После замыкания ключа начинается процесс разрядки конденсатора через катушку, в которой возникает ЭДС самоиндукции, препятствующая разрядному току. В катушке появляется магнитное поле, которое становится максимальным при полной разрядке конденсатора Энергия электрического поля преобразуется в энергию магнитного поля:
Далее ток начинает уменьшаться, возникает ЭДС самоиндукции, теперь поддерживающая уменьшающийся ток разряда. Конденсатор перезарядится до первоначального напряжения, но электрическое поле будет противоположного направления. Произойдет обратное преобразование энергии магнитного поля в энергию электрического поля. В дальнейшем процессы будут повторяться в обратном направлении, и в конечном итоге колебательная система вернется в исходное состояние. Если активное сопротивление колебательного контура R равно нулю, описанные выше колебания называются собственными электрическими колебаниями.
Период собственных колебаний определяется по формуле
а частота и циклическая (круговая) частоты, соответственно, равны:
Величина w 0 называется собственной частотой колебательного контура. В замкнутом колебательном контуре (Рис. 2), включающем в себя сопротивление R, индуктивность L и емкость C, по второму закону Кирхгофа сумма падений напряжения равна сумме ЭДС:
а, выразив напряжение на конденсаторе и ток в контуре через заряд
получаем дифференциальное уравнение второго порядка, связывающее заряд на обкладках конденсатора со временем:
Поделив на L и введя обозначения
При отсутствии активного сопротивления R это уравнение упрощается:
и его решением являются уравнения гармонических колебаний заряда, напряжения на конденсаторе и силы тока в контуре
Показатель b называется коэффициентом затухания, и его можно определить из следующего отношения последующих амплитуд:
Логарифм этого отношения называется логарифмическим декрементом затухания и равен:
где
а, следовательно,
и отсюда получаем формулу для экспериментального определения d
Описанные выше рассуждения верны для небольших сопротивлений R, т.е. при которых выполняется условие
Практические задания
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 820; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.137.40 (0.012 с.) |

 Для наблюдения фигур Лиссажу необходимо на одни пластины осциллографа подать сигнал со звукового генератора, а на другие – с переменного выхода источника тока ВС-24 (Рис. 8). Простейшая фигура – эллипс получается при совпадении частот двух источников, причем при точном совпадении эллипс не должен вращаться. Если эллипс вращается, это означает, что частоты немного не совпадают и разность фаз колебаний плавно меняется. Если частоты складываемых колебаний отличаются в целое число раз (в 2, в 3 и т.д.) то на экране осциллографа при определенной разности фаз получается вертикальная или горизонтальная восьмерка с двумя, тремя и более петлями.
Для наблюдения фигур Лиссажу необходимо на одни пластины осциллографа подать сигнал со звукового генератора, а на другие – с переменного выхода источника тока ВС-24 (Рис. 8). Простейшая фигура – эллипс получается при совпадении частот двух источников, причем при точном совпадении эллипс не должен вращаться. Если эллипс вращается, это означает, что частоты немного не совпадают и разность фаз колебаний плавно меняется. Если частоты складываемых колебаний отличаются в целое число раз (в 2, в 3 и т.д.) то на экране осциллографа при определенной разности фаз получается вертикальная или горизонтальная восьмерка с двумя, тремя и более петлями.
 ,
, ,
,
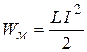 .
.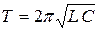 ,
, .
.
 ,
, ,
, .
. и
и  , получаем окончательное уравнение:
, получаем окончательное уравнение: .
. ,
,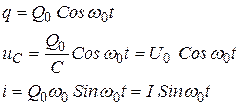 .
. ,
, где
где  , а график колебаний представляет собой косинусоиду с плавно уменьшающейся амплитудой
, а график колебаний представляет собой косинусоиду с плавно уменьшающейся амплитудой  (Рис. 3).
(Рис. 3). .
.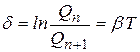 ,
, – период затухающих колебаний. Логарифмический декремент затухания можно определить и другим способом. Если обозначить t время, за которое амплитуда колебаний уменьшится в e раз, то
– период затухающих колебаний. Логарифмический декремент затухания можно определить и другим способом. Если обозначить t время, за которое амплитуда колебаний уменьшится в e раз, то ,
, ,
, .
. .
. . Если же сопротивление велико, и
. Если же сопротивление велико, и  то электрических колебаний в контуре не возникает вовсе, а напряжение на конденсаторе по экспоненте спадает до нуля. Это происходит, при сопротивлениях, больших критического сопротивления Rкр, удовлетворяющего условию:
то электрических колебаний в контуре не возникает вовсе, а напряжение на конденсаторе по экспоненте спадает до нуля. Это происходит, при сопротивлениях, больших критического сопротивления Rкр, удовлетворяющего условию: .
.


