
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила выполнения работы и офрмления полученных результатовСодержание книги
Поиск на нашем сайте
ВВЕДЕНИЕ В методических указаниях приведены описания цикла лабораторных работ по разделу "Электричество и магнетизм" курса общей физики, разработанного коллективом кафедры общей и экспериментальной физики РГПУ им. А.И. Герцена. Электромагнитное взаимодействие является одним из фундаментальных взаимодействий, электрические и магнитные закономерности наиболее широко используются в научной и промышленной деятельности, поэтому при изучении именно раздела "Электричество и магнетизм" особую ценность приобретает лабораторный практикум. Пособие призвано оказать помощь студентам при изучении теоретического курса, стимулировать самостоятельную работу студентов с учебной и справочной литературой и способствовать приобретению навыков получения и обработки экспериментальных данных. Содержание лабораторных работ подобрано таким образом, чтобы по возможности равномерно осветить все основные разделы курса "Электричество и магнетизм": электростатика, постоянный ток, электромагнитные колебания. Одна из работ посвящена изучению принципа действия осциллографа. Описание каждой работы содержит формулировку цели работы, указание разделов, знание которых необходимо для выполнения работы, краткие сведения из теории изучаемого явления, перечень экспериментальных заданий и рекомендаций по их выполнению. Предлагаемые методические указания могут быть использованы при выполнении лабораторного практикума как студентами физического факультета, так и студентами других естественнонаучных направлений при изучении раздела "Электричество и магнетизм" в курсе общей физики.
Правила выполнения работы и офрмления полученных результатов Для получения допуска к выполнению работы студент должен продемонстрировать знание изучаемого явления, понимание методики используемого эксперимента, представить протокол выполнения работы, выполненный в тетради для лабораторных работ и содержащий: 1. название и цель работы; 2. доэкспериментальные данные и предварительные расчеты (при необходимости); 3. перечень заданий (в каждом – электрическая схема, параметры используемых приборов, расчетные формулы, таблицы измерений). Доэкспериментальные данные должны содержать физические константы и табличные величины, которые необходимы для расчетов. Предварительные расчеты подразумевают вычисление величин, которые понадобятся при выполнении работы или которые необходимо проверить в ходе работы. При выборе электроизмерительных приборов необходимо указать требуемые параметры: предел измерения, внутреннее сопротивление (или предельный ток), цену деления для определения погрешности измерения. При выборе элементов схемы нужно указать их номинальные значения (напряжения, тока, мощности, сопротивления). Расчетную формулу необходимо записать так, чтобы она содержала только экспериментально измеренные величины, табличные величины и константы, величины, определенные в предыдущем задании или полученные рассчетно. В таблице нужно предусмотреть графы для непосредственно измеряемых величин (если производится серия измерений), для величин, которые получаются путем произведения каких-либо операций с измеренными величинами (например, по измеренным сериям значений напряжения и тока можно рассчитать серию соответствующих им сопротивлений). В "шапке" таблицы обязательно указывать, в каких единицах измеряется данная величина. После выполнения работы студент обязан представить отчет, который оформляется в той же лабораторной тетради как продолжение протокола работы. Отчет должен содержать: 1. результат выполнения каждого задания с заполненными таблицами, определенными величинами, построенными графиками; 2. окончательный результат, полученный после выполнения всех заданий (если он требуется для достижения цели работы); 3. краткий вывод по результатам работы (определена величина, подтверждена зависимость, исследовано явление и т.д.). Если необходимо по ходу работы построить график, он должен быть построен на миллиметровой бумаге в необходимом масштабе (т.е. захватывать всю область экспериментальных значений, с ценой деления каждой оси много меньше измеряемой величины) с обязательным указанием единиц измерения отложенных на осях величин. Каждая измеренная величина должна быть приведена с погрешностью измерения, каждая определенная по графику величина также должна учитывать погрешность, задаваемую ценой деления осей графика. Соответственно, и каждая рассчитанная величина обязательно должна быть указана с погрешностью, включающей в себя все погрешности измерений и графиков. Вывод должен содержать краткое описание исследуемого явления, закономерности, характеристику эффективности использованного метода исследования. Необходимо привести (если возможно) табличные или номинальные значения определенных экспериментально или рассчитанных по экспериментальным данным величин. Рекомендуемая литература 1. Сивухин Д.В. Общий курс физики. Электричество: – М.: Наука, 1998. – Т.3. 2. Савельев И.В. Курс общей физики. – М.: Наука, 1987, Т.2. 3. Калашников С.Г. Электричество: – М.: Наука, 1977. 4. Матвеев А.Н. Электричество и магнетизм. – М.: Высшая школа, 1979. 5. Фриш С.Э., Тиморева А.Б. Курс общей физики. М.: Наука, 1951. – Т.2 6. Лабораторная работа № 1 Методы ограничения и регулировки тока и напряжения Цель работы. Изучить методы регулировки тока и напряжения в цепях постоянного тока. Знания, необходимые для допуска к работе. – Закон Ома для участка цепи постоянного тока; – Закономерности последовательного и параллельного соединения сопротивлений. Краткие сведения из теории. Любые электрические приборы рассчитаны на определенные значения мощности, выделяемой на них при протекании тока (так называемую номинальную мощность), а соответственно, на номинальные значения тока и напряжения. Для ограничения и регулировки силы тока в цепях постоянного тока применяются специальные регулируемые сопротивления – реостаты, включаемые в цепь либо в варианте собственно реостата, либо в варианте потенциометра.  Изменять силу тока, протекающего по цепи при неизменном выходном напряжении источника тока, можно, меняя общее сопротивление цепи. Для этого реостат включается в электрическую цепь последовательно с сопротивлением нагрузки R (Рис. 1). В этом случае, сила тока может меняться в пределах от Изменять силу тока, протекающего по цепи при неизменном выходном напряжении источника тока, можно, меняя общее сопротивление цепи. Для этого реостат включается в электрическую цепь последовательно с сопротивлением нагрузки R (Рис. 1). В этом случае, сила тока может меняться в пределах от  , когда движок реостата находится в крайнем левом положении (1) и сопротивление включенной в цепь части реостата равно нулю, а значит, общее сопротивление цепи определяется сопротивлением нагрузки, до , когда движок реостата находится в крайнем левом положении (1) и сопротивление включенной в цепь части реостата равно нулю, а значит, общее сопротивление цепи определяется сопротивлением нагрузки, до  , когда движок находится в крайнем правом положении (2) и весь реостат включен в цепь. Очевидно, что при изменении тока, протекающего через нагрузку, будет изменяться и напряжение на ней , когда движок находится в крайнем правом положении (2) и весь реостат включен в цепь. Очевидно, что при изменении тока, протекающего через нагрузку, будет изменяться и напряжение на ней  . Недостатком реостата является то, что он не позволяет уменьшать ток в цепи и напряжение на нагрузочном сопротивлении до нуля. . Недостатком реостата является то, что он не позволяет уменьшать ток в цепи и напряжение на нагрузочном сопротивлении до нуля.
Практические задания Вопросы к зачету по работе. – Как по известным значениям номинальной мощности и сопротивления определить номинальные силу тока и напряжение? – Чему равны общие сопротивления последовательно или параллельно соединенных проводников? – Как рассчитать общее сопротивление смешанного соединения проводников? – 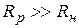 и и  при выборе реостата и потенциометра. при выборе реостата и потенциометра.
Лабораторная работа № 2 Методы расширения пределов измерения Цель работы. Изучить методы расширения пределов измерения амперметра и вольтметра. Краткие сведения из теории. Для расширения пределов измерения электроизмерительных приборов применяют методы последовательного или параллельного подключения к приборам сопротивлений, изменяющих силу тока в цепи или напряжение на зажимах прибора.
 , ,
а сумма токов текущих через амперметр и через шунт равна полному току в электрической цепи:
Отсюда следует метод расчета шунтирующего сопротивления:
откуда
где
а напряжения на сопротивлении вольтметра и на добавочном сопротивлении пропорциональны величинам их сопротивлений:
Несложный вывод позволяет определить необходимую величину добавочного сопротивления: 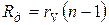 . .
Амперметр с шунтирующим сопротивлением и вольтметр с добавочным сопротивлением следует рассматривать как новые приборы с расширенными пределами измерения. Практические задания 1. Расширение пределов измерения амперметра до ~ 10 ¸ 100 мА. По номинальным значениям цены деления по току CI и внутреннего сопротивления r G школьного демонстрационного гальванометра, указанным на гальванометрической шкале, можно определить предельный ток гальванометра
Выбрав напряжение источника тока U 0, необходимо рассчитать сопротивление, которое включается в цепь для создания тока I 0:
 , где N – деление шкалы гальванометра. , где N – деление шкалы гальванометра.
2. Расширение пределов измерения вольтметра до ~ 1 ¸ 10 В. Зная номинальные значения внутреннего сопротивления r G и предельное значение тока гальванометра I G, определить предел измерения гальванометра по напряжению
Зная U 0, необходимо выбрать контрольный вольтметр с пределом измерения ³ U 0. Собрать схему (Рис. 4), выставить по контрольному вольтметру требуемое напряжение U 0, и, если есть необходимость, скорректировать величину добавочного сопротивления так, чтобы стрелка гальванометра отклонилась на последнее деление. Отградуировать полученный вольтметр по контрольному прибору, меняя напряжение на источнике, и построить график соответствия напряжения делениям гальванометра Проанализировать полученные графики и сделать вывод о рабочих характеристиках полученных электроизмерительных приборов с расширенными пределами измерения. Вопросы к зачету по работе. – Объяснить устройство и принцип действия электроизмерительных приборов магнитоэлектрической, электромагнитной и электродинамической систем. – Почему последовательное или параллельное подключение сопротивления меняет пределы измерения электроизмерительных приборов? – Лабораторная работа № 3 Методы экспериментального определения Цель работы. Изучить метод амперметра и вольтметра и мостовой метод определения сопротивления. Краткие сведения из теории.
 , и, соответственно, дает завышенные показания. Величина этой погрешности равна , и, соответственно, дает завышенные показания. Величина этой погрешности равна 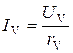 и будет тем меньше, чем больше сопротивление вольтметра по сравнению с исследуемым сопротивлением, т.е. чем меньший ток будет идти через вольтметр. Поэтому данный вариант подключения электроизмерительных приборов используется при измерении небольших сопротивлений и будет тем меньше, чем больше сопротивление вольтметра по сравнению с исследуемым сопротивлением, т.е. чем меньший ток будет идти через вольтметр. Поэтому данный вариант подключения электроизмерительных приборов используется при измерении небольших сопротивлений  . .
Для измерения больших сопротивлений используется другой способ подключения (Рис.1, б). В этом случае уже вольтметр измеряет не напряжение на неизвестном сопротивлении, а сумму напряжений на сопротивлении амперметра и неизвестном сопротивлении Ясно, что желательно при выборе электроизмерительных приборов соблюсти оба условия для их сопротивлений, и тогда обе схемы дадут достаточно высокую точность определения неизвестного сопротивления.
Гальванометр показывает отсутствие тока если:
Эти равенства можно записать через токи, текущие соответственно в ветви сравнения и неизвестного сопротивления и ветви соотношения моста,
а, поделив почленно эти равенства друг на друга, получаем условие равновесия моста:  , ,
откуда выводим формулу для расчета неизвестного сопротивления:
Если сопротивления плеч соотношения R 1 и R 2 равны, такой мост называется равноплечным, и позволяет измерить неизвестное сопротивления с наибольшей точностью. Но использовать равноплечный мост возможно не всегда, например, когда сопротивление плеча сравнения заведомо меньше неизвестного сопротивления, приходится использовать разноплечный мост с известным соотношением плеч Практические задания Вопросы к зачету по работе. – Почему электроизмерительные приборы обладают сопротивлением? – Какие искажения вносят в измеряемые величины электроизмерительные приборы и как уменьшить или учесть эти искажения? – В чем заключается физический принцип мостового метода измерения сопротивлений? – Лабораторная работа № 4 Цель работы. Получить и изучить энергетические соотношения в замкнутых цепях постоянного тока. Краткие сведения из теории. Замкнутая электрическая цепь должна содержать, как минимум, источник тока и нагрузку (внешнее сопротивление R). Источник тока характеризуется наличием ЭДС e и внутреннего сопротивления r. Соответственно, закон Ома для замкнутой (полной) цепи выглядит следующим образом:
Полная мощность, выделяющаяся в замкнутой цепи, рассчитывается по формуле:
Раскрыв скобки, получаем сумму полезной мощности
Подставив в выражение для полезной мощности значение силы тока из закона Ома, получаем формулу зависимости полезной мощности от параметров источника тока и нагрузочного сопротивления:
Из анализа этой формулы следует, что при сопротивлениях нагрузки R значительно меньше внутреннего сопротивления источника r знаменатель не будет сильно меняться, и полезная мощность будет возрастать приблизительно пропорционально сопротивлению нагрузки. При значительных значениях внешнего сопротивления знаменатель возрастает практически пропорционально квадрату сопротивления R, и, соответственно, полезная мощность обратно пропорциональна сопротивлению нагрузки. Можно найти, где находится максимальное значение полезной мощности, взяв первую производную от приведенной выше формулы и приравняв ее нулю:
Очевидно, что максимальное значение полезной мощности достигается при согласовании нагрузки с внутренним сопротивлением источника тока
При этом полная мощность, равная сумме полезной мощности и мощности, теряемой на внутреннем сопротивлении источника, вдвое больше:
и, соответственно, КПД равен 50%. При увеличении сопротивлении нагрузки, устремлении его к бесконечности, КПД стремится к 100%  , ,
но полезная мощность при этом стремится к нулю, и источник никакой полезной работы не совершает. Потери мощности из-за несогласованности нагрузки и внутреннего сопротивления источника характеризуются величиной
Практические задания Вопросы к зачету по работе. – Почему на нагрузке выделяется энергия при протекании тока, сколько ее выделяется и на что она тратится? – Почем не вся мощность, вырабатываемая источником тока, может быть использована в качестве полезной мощности, и как уменьшить потери мощности? – Что означает "согласованная нагрузка" и чему равен КПД источника при согласовании нагрузки? – Лабораторная работа № 5 Изучение компенсационного метода измерения Цель работы. Изучить компенсационный метод измерения напряжений, токов и сопротивлений. Краткие сведения из теории. ЭДС источника тока нельзя точно измерить вольтметром (только если вольтметр не электростатической системы), потому что вольтметр имеет конечное сопротивление, а значит, при подключении его к источнику в замкнутом контуре потечет ток и часть напряжение будет падать на внутреннем сопротивлении источника. Вольтметр же измерит только внешнее падение напряжения, причем оно будет тем меньше, чем меньше сопротивление вольтметра по сравнению с сопротивлением источника. Компенсационный метод измерения позволяет измерять электрические параметры цепей с высокой точностью, как правило, не достижимой при использовании амперметров, вольтметров, гальванометров и т.д.
 , то окончательная формула для определения неизвестного ЭДС выглядит так: , то окончательная формула для определения неизвестного ЭДС выглядит так:
Добиться компенсации можно, меняя напряжение опорного источника U 0 при неизменном положении движка реостата R, или при фиксированном напряжении U 0 перемещая движок до наступления компенсации. Часто невозможно достичь желаемой точности в определении напряжения опорного источника U 0 и параметров компенсирующей цепи R и R 1. Тогда можно воспользоваться относительным методом, взяв в качестве эталонного ЭДС нормальный элемент. Его достоинством является высокая точность и стабильность выходной ЭДС. При комнатной температуре (~ 20°С)
Ясно, что данный метод компенсации позволяет измерять неизвестное ЭДС только при условии В компенсационных схемах повышенной точности вместо измерительного сопротивления R используется набор декад образцовых сопротивлений, причем подключение их выполнено таким образом, чтобы сила тока в цепи опорного источника I 0 оставалась неизменной. Тогда эти декады сопротивлений можно проградуировать по эталонному источнику в единицах напряжения и снимать показания сразу в этих единицах. Компенсационный метод позволяет измерять, правда косвенно, и ток, и сопротивление. При измерении сопротивления его и эталонное сопротивление включают последовательно. При протекании по ним тока I падение напряжения пропорционально величинам их сопротивлений  , ,
а почленно поделив эти выражения друг на друга, получаем формулу для определения неизвестного сопротивления:
По падению напряжения на эталонном сопротивлении можно точно определить силу тока Ix, протекающего в цепи,
Компенсационные методы могут быть использованы и для калибровки и градуировки электроизмерительных приборов. Практические задания Вопросы к зачету по работе. – Почему невозможно измерить ЭДС источника тока вольтметром магнитоэлектрической системы. – Объяснить физическую суть компенсационного метода измерений электрических величин. – Почему компенсационный метод позволяет точно измерить ЭДС источника тока? – Как, используя компенсационный метод, произвести измерение силы тока в цепи и величину сопротивления нагрузки? – Объяснить устройство и принцип действия измерительного потенциометра ПП-63.
Лабораторная работа № 6 Цель работы. Изучить закономерности протекания квазистационарных токов на примере токов зарядки и разрядки конденсатора. Краткие сведения из теории. Отличие квазистационарных токов от постоянного тока в том, что изменение тока происходит достаточно медленно, так, что в каждый момент времени для электрических величин, описывающих состояние системы, выполняются все закономерности, характерные для постоянного тока.
где Iз – мгновенный ток зарядки, U – мгновенное значение напряжения на пластинах конденсатора. Напряжение на конденсаторе и зарядный ток соответственно равны:
Решаем его относительно мгновенного значения напряжения
где A и Тогда выражения для мгновенного напряжения на конденсаторе и мгновенного тока в контуре примут вид:
Видно, что в момент замыкания ключа ток практически мгновенно достигает значения При разрядке конденсатора через сопротивление наблюдаются следующие процессы. В момент замыкания ключа в нижнее положение (2) в цепи потечет ток, вызванный наличием напряжения на обкладках конденсатора
При этом мгновенные значения тока и напряжения будут равны:  . .
Знак "–" в формуле для тока показывает, что выбранное положительное направление тока соответствует уменьшению заряда конденсатора. Эта система уравнений решаются аналогично случаю зарядки конденсатора. Получается выражение:
откуда
Опять же из начальных условий
Мгновенный ток, как в случае зарядки, так и в случае разрядки конденсатора определяется формулой:
Из приведенных выше рассуждений видно, что зарядка и разрядка конденсатора происходит не мгновенно, а в течение некоторого времени. Скорость установления напряжения на конденсаторе зависит от R и C. Величина, постоянная для данного контура, Практические задания Предварительный расчет параметров зарядной и разрядной цепи.  . .
Вопросы к зачету по работе. – Теоретически вывести закономерности изменения зарядного тока и напряжения со временем – Почему при зарядке и разрядке конденсатора в цепи протекает ток, хотя пластины конденсатора разделены диэлектриком, т.е. цепь не замкнута? – Физический смысл постоянной времени зарядки и разрядки конденсатора t. – От чего зависит величина заряда конденсатора и методы определения заряда? – Объяснить устройство и принцип действия вольтметра электростатической системы.
Лабораторная работа № 7 Цель работы. Изучить механизмы поляризации диэлектриков в электрических полях, характеристики диэлектрических свойств. Краткие сведения из теории. Диэлектрики, как и все другие вещества, состоят из частиц (атомов или молекул). Отличительной чертой диэлектриков является то, что в них отсутствуют свободные заряды, а все имеющиеся заряды связаны (носители заряда могут перемещаться на расстояния, сравнимые с размерами атома). Диэлектрики можно разделить на два класса: неполярные и полярные. В неполярных диэлектриках структурные единицы, из которых они состоят, не обладают собственным дипольным моментом. Например, если электроны расположены вокруг атома симметрично, то геометрический центр отрицательного заряда совпадает с расположением ядра атома, т.е. положительного заряда, и такой атом не обладает собственным дипольным моментом. У большинства диэлектриков такой симметрии между отрицательными и положительными зарядами не наблюдается, в результате каждый атом или молекула обладает собственным дипольным моментом. Но и полярные диэлектрики в целом не обладают собственным электрическим полем, так как дипольные моменты отдельных атомов расположены хаотически друг относительно друга вследствие хаотического теплового движения.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.240.14 (0.011 с.) |

 Подключением реостата в электрическую цепь в качестве делителя напряжения (Рис. 2) также можно менять напряжение на нагрузочном сопротивлении, а значит и ток, протекающий через него. В данном случае реостат называют потенциометром и подключают его параллельно цепи, содержащей нагрузочное сопротивление R. При данном методе подключения движок делит потенциометр на две части, на нагрузку приходится напряжение, снимаемое с подключенной параллельно части потенциометра, и оно меняется от нуля, когда движок в крайнем левом положении (1), до U 0, когда движок в крайнем правом положении (2).
Подключением реостата в электрическую цепь в качестве делителя напряжения (Рис. 2) также можно менять напряжение на нагрузочном сопротивлении, а значит и ток, протекающий через него. В данном случае реостат называют потенциометром и подключают его параллельно цепи, содержащей нагрузочное сопротивление R. При данном методе подключения движок делит потенциометр на две части, на нагрузку приходится напряжение, снимаемое с подключенной параллельно части потенциометра, и оно меняется от нуля, когда движок в крайнем левом положении (1), до U 0, когда движок в крайнем правом положении (2). Если сила тока, протекающего в цепи, превышает предельно допустимый ток амперметра, то для того, чтобы этот амперметр можно было использовать в данной цепи, применяется метод шунтирования (Рис. 1). Он заключается в подключении параллельно амперметру шунтирующего сопротивления Rш. В этом случае часть тока пойдет через амперметр, а часть – по шунтирующему сопротивлению, причем соотношение токов, текущих через шунтирующее сопротивление и через амперметр, обратно пропорционально соотношению сопротивлений амперметра и шунта:
Если сила тока, протекающего в цепи, превышает предельно допустимый ток амперметра, то для того, чтобы этот амперметр можно было использовать в данной цепи, применяется метод шунтирования (Рис. 1). Он заключается в подключении параллельно амперметру шунтирующего сопротивления Rш. В этом случае часть тока пойдет через амперметр, а часть – по шунтирующему сопротивлению, причем соотношение токов, текущих через шунтирующее сопротивление и через амперметр, обратно пропорционально соотношению сопротивлений амперметра и шунта: .
. ,
,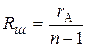 ,
,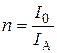 , коэффициент, показывающий, во сколько раз ток в цепи превышает предельный ток амперметра.
, коэффициент, показывающий, во сколько раз ток в цепи превышает предельный ток амперметра.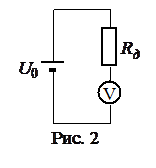 Для расширения пределов измерения вольтметра используется последовательное подключение к нему добавочного сопротивления, которое вместе с сопротивлением вольтметра образует фиксированный делитель напряжения (Рис. 2). Коэффициент деления должен соответствовать отношению напряжения, которое необходимо измерить, и предельному напряжению вольтметра
Для расширения пределов измерения вольтметра используется последовательное подключение к нему добавочного сопротивления, которое вместе с сопротивлением вольтметра образует фиксированный делитель напряжения (Рис. 2). Коэффициент деления должен соответствовать отношению напряжения, которое необходимо измерить, и предельному напряжению вольтметра 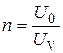 . Полное напряжение равно сумме напряжений на вольтметре и добавочном сопротивлении
. Полное напряжение равно сумме напряжений на вольтметре и добавочном сопротивлении ,
, .
.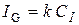 , где k – число делений шкалы, и, зная силу тока, которую необходимо измерить I 0, рассчитать сопротивление шунта:
, где k – число делений шкалы, и, зная силу тока, которую необходимо измерить I 0, рассчитать сопротивление шунта: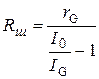 .
. . Потом надо выбрать контрольный амперметр с пределом ³ I 0.
. Потом надо выбрать контрольный амперметр с пределом ³ I 0. Собрать схему (Рис. 3), по контрольному амперметру выставить силу тока, заданную преподавателем, и убедиться, что гальванометр с рассчитанным шунтом показывает полное отклонение, т.е. имеет предел измерения, соответствующий именно I 0. Если при этом токе отклонение стрелки гальванометра не максимально (крайнее деление) или выходит за пределы шкалы, то необходимо экспериментально скорректировать величину сопротивления шунта.
Собрать схему (Рис. 3), по контрольному амперметру выставить силу тока, заданную преподавателем, и убедиться, что гальванометр с рассчитанным шунтом показывает полное отклонение, т.е. имеет предел измерения, соответствующий именно I 0. Если при этом токе отклонение стрелки гальванометра не максимально (крайнее деление) или выходит за пределы шкалы, то необходимо экспериментально скорректировать величину сопротивления шунта. . Получив у преподавателя значение U 0, рассчитать величину добавочного сопротивления:
. Получив у преподавателя значение U 0, рассчитать величину добавочного сопротивления: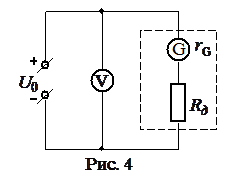
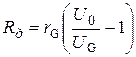 .
. .
. Для определения электрического сопротивления можно воспользоваться законом Ома для участка цепи, содержащего измеряемое сопротивление. Достаточно измерить падение напряжения на сопротивлении и силу тока, протекающего по нему. Но, в силу того, что электроизмерительные приборы также обладают сопротивлением, включение их в электрическую цепь приведет к изменению тока и падения напряжения на остальных элементах цепи, в том числе – и на исследуемом сопротивлении. Причем, в зависимости от того, как подключены амперметр и вольтметр, выдавать искаженные данные будет либо один, либо другой прибор.
Для определения электрического сопротивления можно воспользоваться законом Ома для участка цепи, содержащего измеряемое сопротивление. Достаточно измерить падение напряжения на сопротивлении и силу тока, протекающего по нему. Но, в силу того, что электроизмерительные приборы также обладают сопротивлением, включение их в электрическую цепь приведет к изменению тока и падения напряжения на остальных элементах цепи, в том числе – и на исследуемом сопротивлении. Причем, в зависимости от того, как подключены амперметр и вольтметр, выдавать искаженные данные будет либо один, либо другой прибор. . В таком варианте подключения желательно, чтобы выполнялось условие
. В таком варианте подключения желательно, чтобы выполнялось условие  . Тогда падение напряжения на сопротивлении амперметра
. Тогда падение напряжения на сопротивлении амперметра 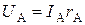 будет незначительным, и показания вольтметра можно считать достаточно точными.
будет незначительным, и показания вольтметра можно считать достаточно точными. Другим методом измерения сопротивлений является мостовой метод. Простейший мост содержит источник питания, плечи соотношения R 1 и R 2, плечо сравнения Rср и плечо, в которое включается неизвестное сопротивление Rx, гальванометр (индикатор нуля). Методика измерения состоит в приведении к нулю разности потенциалов в точках двух параллельных ветвей, к которым подключен гальванометр. Это достигается или смещением движка потенциометра, т.е. изменением соотношения плеч (линейный мост – Рис. 2, а), или изменением величины сопротивления плеча сравнения при неизменном соотношении плеч (магазинный мост – Рис. 2, б).
Другим методом измерения сопротивлений является мостовой метод. Простейший мост содержит источник питания, плечи соотношения R 1 и R 2, плечо сравнения Rср и плечо, в которое включается неизвестное сопротивление Rx, гальванометр (индикатор нуля). Методика измерения состоит в приведении к нулю разности потенциалов в точках двух параллельных ветвей, к которым подключен гальванометр. Это достигается или смещением движка потенциометра, т.е. изменением соотношения плеч (линейный мост – Рис. 2, а), или изменением величины сопротивления плеча сравнения при неизменном соотношении плеч (магазинный мост – Рис. 2, б). .
.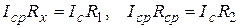 ,
,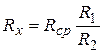 .
. . Возможны ситуации, когда необходимо пользоваться мостом с соотношением плеч < 1.
. Возможны ситуации, когда необходимо пользоваться мостом с соотношением плеч < 1.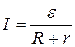 .
.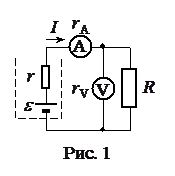 При включении в электрическую цепь электроизмерительных приборов их сопротивление необходимо включить в общее внешнее сопротивление, т.е. наличие приборов приводит к изменению сопротивления нагрузки R (Рис. 1).
При включении в электрическую цепь электроизмерительных приборов их сопротивление необходимо включить в общее внешнее сопротивление, т.е. наличие приборов приводит к изменению сопротивления нагрузки R (Рис. 1). .
.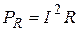 , выделяющейся на нагрузке, и
, выделяющейся на нагрузке, и 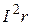 – мощности, теряющейся на внутреннем сопротивлении источника тока и идущей на его нагрев.
– мощности, теряющейся на внутреннем сопротивлении источника тока и идущей на его нагрев.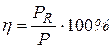 .
. .
.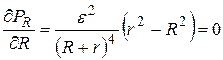 .
.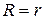 и равно
и равно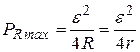 .
. ,
,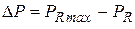 , а относительные потери мощности определяются выражением:
, а относительные потери мощности определяются выражением: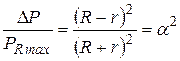 .
. Идея метода заключается в следующем. Падение напряжения на участке сопротивления R 1, возникающее при протекании тока, включается навстречу подключенному параллельно неизвестному источнику ЭДС. При этом, если выполнится условие
Идея метода заключается в следующем. Падение напряжения на участке сопротивления R 1, возникающее при протекании тока, включается навстречу подключенному параллельно неизвестному источнику ЭДС. При этом, если выполнится условие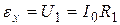 ,
,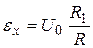 .
. .
. .
. .
. .
. Процессы зарядки и разрядки конденсатора, в этом смысле, можно отнести к квазистационарным. Эти процессы проиллюстрированы на схеме (Рис. 1). Рассмотрим процесс зарядки. Ключ замыкается в верхнее положение (1). По правилу Кирхгофа для верхнего контура
Процессы зарядки и разрядки конденсатора, в этом смысле, можно отнести к квазистационарным. Эти процессы проиллюстрированы на схеме (Рис. 1). Рассмотрим процесс зарядки. Ключ замыкается в верхнее положение (1). По правилу Кирхгофа для верхнего контура ,
, .
. .
.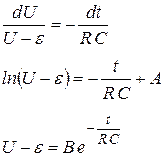 ,
, – некоторые константы. Из начального условия
– некоторые константы. Из начального условия  можно определить
можно определить 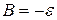 .
.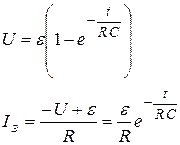 .
.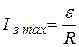 , а потом по экспоненциальному закону спадает до нуля при
, а потом по экспоненциальному закону спадает до нуля при  .
. .
. ,
, .
. определяется
определяется  , и формула мгновенного напряжения на обкладках конденсатора принимает окончательный вид:
, и формула мгновенного напряжения на обкладках конденсатора принимает окончательный вид: .
.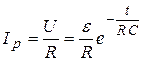 .
. называется постоянной времени данного контура (или временем релаксации) и показывает, через какое время после выключения e напряжение на конденсаторе уменьшится в
называется постоянной времени данного контура (или временем релаксации) и показывает, через какое время после выключения e напряжение на конденсаторе уменьшится в


