
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение неизвестной ЭДС методом компенсации.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Произвести компенсацию неизвестного источника при положении ключа "влево". Рассчитать ЭДС неизвестного источника по формуле:
Переключением ключа "вправо" подключить к измерительной схеме эталонный источник и перемещением движка добиться компенсации eэ падением напряжения на участке реохорда l 2 э . Рассчитать уточненное значение неизвестной ЭДС 
и сравнить его с полученным ранее. Определение компенсационным методом напряжений, токов и сопротивлений.
Произвести измерения напряжений на неизвестном и эталонном сопротивлениях и определить Ux, Ix, Rx. Сделать выводы о возможности и рациональности использования компенсационных методов измерения электрических характеристик цепей постоянного тока. Вопросы к зачету по работе. – Почему невозможно измерить ЭДС источника тока вольтметром магнитоэлектрической системы. – Объяснить физическую суть компенсационного метода измерений электрических величин. – Почему компенсационный метод позволяет точно измерить ЭДС источника тока? – Как, используя компенсационный метод, произвести измерение силы тока в цепи и величину сопротивления нагрузки? – Объяснить устройство и принцип действия измерительного потенциометра ПП-63.
Лабораторная работа № 6 Исследование процессов зарядки и разрядки конденсатора Цель работы.
Изучить закономерности протекания квазистационарных токов на примере токов зарядки и разрядки конденсатора. Знания, необходимые для допуска к работе. – Квазистационарные токи; – Правила Кирхгофа; – Емкостное сопротивление конденсатора. Краткие сведения из теории. Отличие квазистационарных токов от постоянного тока в том, что изменение тока происходит достаточно медленно, так, что в каждый момент времени для электрических величин, описывающих состояние системы, выполняются все закономерности, характерные для постоянного тока.
где Iз – мгновенный ток зарядки, U – мгновенное значение напряжения на пластинах конденсатора. Напряжение на конденсаторе и зарядный ток соответственно равны:
Решаем его относительно мгновенного значения напряжения
где A и Тогда выражения для мгновенного напряжения на конденсаторе и мгновенного тока в контуре примут вид:
Видно, что в момент замыкания ключа ток практически мгновенно достигает значения При разрядке конденсатора через сопротивление наблюдаются следующие процессы. В момент замыкания ключа в нижнее положение (2) в цепи потечет ток, вызванный наличием напряжения на обкладках конденсатора
При этом мгновенные значения тока и напряжения будут равны:  . .
Знак "–" в формуле для тока показывает, что выбранное положительное направление тока соответствует уменьшению заряда конденсатора. Эта система уравнений решаются аналогично случаю зарядки конденсатора. Получается выражение:
откуда
Опять же из начальных условий
Мгновенный ток, как в случае зарядки, так и в случае разрядки конденсатора определяется формулой:
Из приведенных выше рассуждений видно, что зарядка и разрядка конденсатора происходит не мгновенно, а в течение некоторого времени. Скорость установления напряжения на конденсаторе зависит от R и C. Величина, постоянная для данного контура, Практические задания Предварительный расчет параметров зарядной и разрядной цепи.  . .
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 502; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.212.245 (0.011 с.) |

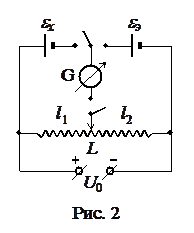 В качестве измерительного сопротивления можно использовать реохорд, сопротивление которого R пропорционально длине l. В целях недопущения перегрева реохорда напряжение опорного источника U 0 не должно превышать 2 В. Источником опорного напряжения служит ИЭПП–1. Для того, чтобы не было необходимости в ходе работы менять собранную схему, можно неизвестный и эталонный источники ЭДС подключать к измерительной цепи последовательно с использованием трехполюсного ключа (Рис. 2).
В качестве измерительного сопротивления можно использовать реохорд, сопротивление которого R пропорционально длине l. В целях недопущения перегрева реохорда напряжение опорного источника U 0 не должно превышать 2 В. Источником опорного напряжения служит ИЭПП–1. Для того, чтобы не было необходимости в ходе работы менять собранную схему, можно неизвестный и эталонный источники ЭДС подключать к измерительной цепи последовательно с использованием трехполюсного ключа (Рис. 2). .
. В качестве измерителя используется потенциометр ПП–63. Так как предел измерения потенциометра Uп составляет 100 мВ, необходимо рассчитать и собрать измерительную схему (Рис. 3). U 0 опять выбирается 2 В (ИЭПП–1). В качестве эталонного сопротивления можно взять магазин сопротивлений. Ограничительное сопротивление рассчитывается по формуле:
В качестве измерителя используется потенциометр ПП–63. Так как предел измерения потенциометра Uп составляет 100 мВ, необходимо рассчитать и собрать измерительную схему (Рис. 3). U 0 опять выбирается 2 В (ИЭПП–1). В качестве эталонного сопротивления можно взять магазин сопротивлений. Ограничительное сопротивление рассчитывается по формуле: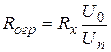 .
. Процессы зарядки и разрядки конденсатора, в этом смысле, можно отнести к квазистационарным. Эти процессы проиллюстрированы на схеме (Рис. 1). Рассмотрим процесс зарядки. Ключ замыкается в верхнее положение (1). По правилу Кирхгофа для верхнего контура
Процессы зарядки и разрядки конденсатора, в этом смысле, можно отнести к квазистационарным. Эти процессы проиллюстрированы на схеме (Рис. 1). Рассмотрим процесс зарядки. Ключ замыкается в верхнее положение (1). По правилу Кирхгофа для верхнего контура ,
, .
. .
.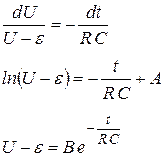 ,
, – некоторые константы. Из начального условия
– некоторые константы. Из начального условия  можно определить
можно определить 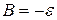 .
.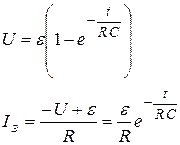 .
.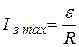 , а потом по экспоненциальному закону спадает до нуля при
, а потом по экспоненциальному закону спадает до нуля при  .
. .
. ,
, .
. определяется
определяется  , и формула мгновенного напряжения на обкладках конденсатора принимает окончательный вид:
, и формула мгновенного напряжения на обкладках конденсатора принимает окончательный вид: .
.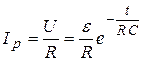 .
. называется постоянной времени данного контура (или временем релаксации) и показывает, через какое время после выключения e напряжение на конденсаторе уменьшится в
называется постоянной времени данного контура (или временем релаксации) и показывает, через какое время после выключения e напряжение на конденсаторе уменьшится в


