
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цикл с неизвестным числом повторенийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Цикл с неизвестным числом повторений называется также итерационным циклом. В языке Турбо Паскаль имеются два оператора цикла - WHILE и REPEAT, которые используются для организации цикла с неизвестным числом повторений. Общая форма конструкции, образующей цикл WHILE,имеет вид: WHILE <выражение> DO <оператор> Здесь WHILE (пока); DO — ключевые слова языка; <выражение> — логическое выражение, которое определяет условие продолжение цикла. Первая строка (оператор WHILE) конструкции называется заголовком цикла. <Оператор> образует тело цикла, состоящее из простого или составного оператора. Выполнение оператора WHILE происходит следующим образом: 1. Вычисляется выражение, указанное в заголовке цикла. 2. Если выражение истинно, то один раз выполняется тело цикла и вновь вычисляется выражение. 3. Пункт 2 повторяется до тех пор, пока выражение истинно. 4. Если выражение ложно, то тело цикла не выполняется, осуществляется выход из цикла, т.е. управление передается оператору, который следует за оператором WHILE. Общий вид записи оператора REPEAT: REPEAT <оператор> UNTIL <выражение> где <оператор> - тело цикла, состоящее из простого или составного оператора; <выражение> - логическое выражение, определяющее окончание цикла. Выполнение оператора WHILE происходит следующим образом: 1. Выполняется тело цикла. 2. Вычисляется выражение, указанное во фразе UNTIL. 3. Если выражение ложно, то повторяются пп. 1 и 2. 4. Если выражение истинно, то выходим из цикла, т.е. управление передается оператору, который следует за оператором REPEAT. Из сказанного следует важное правило: операторы тела цикла WHILE и REPEAT должны изменять выражение, указанное в операторе. В противном случае будет иметь место бесконечный цикл, что противоречит определению алгоритма. В тело итерационного цикла допускается включать другие циклы. Это может быть другой итерационный циклили цикл с известным числом повторений. Другими словами, в итерационных циклах никаких ограничений на вложенные циклы не накладывается. Примеры реализации итерационного цикла Пример 1.15. Составить программу для вычисления функции, заданной рекурсивными формулами: Y 0=(1+ X)/3 Yk +1 = Yk + (X / Yk · Yk - Yk)/3 при k =l, 2, 3.... Вычисления закончить при выполнении условия:
| Yk +l - Yk | < е, где е — точность вычислений (малое положительное число). Аргумент функции Х —произвольное число. Решение. Анализ постановки задачи Исходные данные для решения: аргумент функции — Х и точность вычисления — Е. То, что заданы рекурсивные формулы для вычислений, означает повторяемость (цикличность) вычислений: каждое новое значение функции вычисляется по ее предыдущему значению. Число вычислений неизвестно, но известно условие продолжения вычислений: пока | Yk +1 - Yk | Введем обозначения объектов программы: Y0 — предыдущее(в том числе начальное) значение функции; Y —очередное(в том числе конечное) значение функции; Z — модуль разности значений. Для решения задачи будем использовать цикл WHILE. Как и любой другой, этот цикл требует подготовки. В первую очередь необходимо обеспечить истинность выражения Z Значение Е определим на этапе ввода исходных данных, а значение Z определим до входа в цикл, присвоив ему любое значение, которое больше Е, например Z:=2*E. Также до входа в цикл необходимо вычислить начальное значение функции Y0:=(1+X)/3. Наконец, тело цикла. В нем вычисляется очередное значение функции Y:=Y0+(X/Y0/Y0-Y0)/3. Здесь же необходимо обеспечить изменение значения выражения в заголовке цикла Z:=ABS(Y-Y0). Наконец, необходимо подготовить следующую итерацию Y0:=Y. Выход из цикла произойдет при достижении заданной точности вычислений. После этого можно выводить полученные результаты. С целью большей информативности результатов дополним алгоритм вычислением числа выполненных итераций К:=К+1 Начальное значение К присвоим до цикла К:=1 Результаты вычислений выведем в следующем виде:
Результаты вычислений Аргумент: **.** Заданная точность: *.***** Значение функции: ****.*** Число итераций: *** Поскольку алгоритм уже достаточно детализирован, составим текст программы: Текст программы
PROGRAM Prim115; {Вычисление функции с заданной точностью} VAR X, Y0, Y, E, Z: REAL; K: INTEGER; {Х – Аргумент функции} {Y0, Y – Начальное и конечное значения функции} {Е – Заданная точность} {Z=ABS(Y-Y0)} {K – число итераций} BEGIN {Этап ввода исходных данных} WRITE(‘Аргумент функции’); READLN(X); WRITE(‘Заданная точность вычислений’); READLN(E); {Этап вычислений}
Z:=2*E; Y0:=(1+X)/3; K:=1; WHILE Z>=E DO BEGIN Y:=Y0+(X/Y0/Y0-Y0)/3; Z:=ABS(Y-Y0); Y0:=Y; K:=K+1 END; {Этап вывода результатов} WRITELN(‘Результаты вычислений'); WRITELN(‘Аргумент:’,X:5:2); WRITELN(‘Заданная точность:',E:7:5); WRITELN(‘Значение функции:’,Y:8:3); WRITELN(‘Число итераций:’,K:3); END. Пример 1.16. Вычислить сумму Суммирование прекращать, когда очередной член суммы будет меньше заданного е = 0.0001. Решение. В приведенной ниже программе используется цикл REPEAT: PROGRAM Prim116; VAR X, Eps, S, A: REAL; N: INTEGER; BEGIN X:= 0.5; Eps:=0.0001; S:=0; N:=1; REPEAT A:=cos(n*x)/n; S:=s+a; N:=N+1; UNTIL a<Eps; WRITELN(‘Сумма равна ‘,S:8:5); End.
Пример 1.17. Определить приближенное значение суммы элементов ряда: S = l + x /1! + x 3/3! + x 5/5! +... Суммирование выполнять до тех пор, пока очередное слагаемое не станет меньше заданной величины Е. Решение. Анализ условия задачи Исходными данными для решения задачи являются значения Х и Е, где Е — точность вычислений. Вычисление суммы элементов ряда — цикл с неизвестным числом повторений. Очевидно, что условие выполнения операторов тела цикла можно записать в виде WHILE A>=E DO, где А — очередной элемент ряда; Е — заданная точность вычислений. В теле цикла следует: — накапливать в переменной S значение предыдущего элемента ряда; — получать новое значение элемента ряда. Для вычисления нового элемента ряда необходимо определить закономерность изменения последующего элемента по сравнению с предыдущим. Чтобы найти эту закономерность, попарно сравним соседние элементы и проанализируем выражение, на которое в каждом цикле нужно умножать предыдущий элемент. Результаты сравнения представлены в таблице.
Из приведенной таблицы видно, что числитель выражения от цикла к циклу не меняется: X 2. Знаменатель — произведение двух соседних натуральных чисел, то есть если первое число обозначим переменной К, то в общем виде выражение можно записать: P=X · Х/ (K · (K + 1)), а значение К изменяется в каждом цикле на 2. Итак, WHILE A>=E DO Begin S:=S+A; Р:=Х*X/(К*(К+1)); А:=Р*А; К:=К+2; END; И последнее. До входа в цикл следует определить значения переменных S, А, К: S:=1; А:=Х; К:=2; (см. условие примера) Возможный вариант программы PROGRAM Prim117; VAR X, E, S, A, K, P: REAL; {X – переменная для ввода и хранения аргумента Е – переменная для ввода и хранения точности вычислений S – переменная для получения суммы элементов ряда A – переменная для получения очередного элемента ряда К – переменная для получения знаменателя P – переменная для вычисления значения выражения, на которое умножается предыдущий элемент} {Блок ввода информации} BEGIN WRITE (‘Введите значение аргумента’); READLN(Х); WRITE (‘Введите точность вычислений’); READLN(Е); {Блок вычисления суммы} S:=1; А:=Х; K:=2; WHILE A>=E DO BEGIN S:=S+A; P:=X*X/(К*(К+1)); A:=А*Р; К:=К+2; END; WRITELN(‘При значении аргумента = ’, X); WRITELN(‘Сумма элементов ряда = ’, S) END.
Пример 1.18. Вычислить сумму S = для значений x, изменяющихся в пределах от 0.2 до 1 с шагом 0.2. Суммирование прекращать, когда очередной член суммы по абсолютной величине станет меньше е = 0.0001. Решение. Задача сводится к организации вложенных циклов. Внешний цикл по счетчику обеспечивает изменение х. Во внутреннем цикле по условию осуществляется вычисление суммы. Член суммы an целесообразно представить в виде двух сомножителей:
a n = сn (2 n - 1). Сомножитель cn = (- 1 )n - 1 cn = - cn -1 Число значений х на отрезке от 0.2 до 1 с шагом 0.2 равно 5. В программе для контроля при каждом значении x вычисляется также функция соs x + x sin x, которая приближенно может быть представлена в виде указанной суммы. PROGRAM Prim118; VAR X, S, EPS,C,A: REAL; I, N: INTEGER; BEGIN X:=0.2; Eps:=0.0001; For I:=1 To 5 DO BEGIN S:=1; C:=-1; N:=1; REPEAT C:=-c*x*x/((2*n-1)*2*n); A:=c*(2*n-1); S:=s+a; N:=N+1 UNTIL Abs(a)<Eps; WRITELN(‘x=’,x, ‘ s=’,s, ‘ f(x)=’, cos(x) + x*sin(x)); X:=X+0.2 END End. Пример 1.19. Вычислить сумму ряда Решение. Обозначим объекты программы: S- сумма; N - количество членов ряда; ТЕК - текущий член ряда; PR - предыдущий член ряда. Вычисление данной суммы будем осуществлять в цикле WHILE до тех пор, пока разность по модулю между текущим и предыдущим значениями членов ряда будет больше заданной величины, т.е. WHILE ABS(TEK-PR)>0.04 DO Так как выход из цикла осуществляется при нарушении данного условия, то для вывода правильного значения суммы, в которой разность по модулю между текущим и предыдущим слагаемыми еще остается больше 0,04, следует определить значение суммы, а также значение и номер слагаемого, предшествующего сумме ряда при выходе из цикла. Приведем вариант программы PROGRAM Prim119; VAR S, TEK, PR: REAL; N: INTEGER; BEGIN S:=0.5; ТЕК:=0.5; PR:=0; N:=1; WHILE ABS(TEK-PR)>0.04 DO BEGIN N:=N+1; PR:=TEK; TEK:=1/(2*N); S:=S+TEK; END; WRITELN(‘Сумма= ‘, S-TEK); WRITELN(‘Последнее слагаемое ‘,PR,’ и его номер ’,N-1); END.
Пример 1.20. Найти максимальное количество слагаемых в сумме членов ряда Решение. Введем обозначения объектов: S – сумма; N - количество слагаемых в сумме; А - очередное (текущее слагаемое). Формула общего члена данного ряда имеет вид:
где n - порядковый номер слагаемого. Суммирование осуществляется в цикле WHILE до тех пор, пока сумма остается меньше 12, т.е. WHILE S<12 При выводе результатов следует учесть, что после выхода из цикла значение суммы будет больше или равно 12. Поэтому следует «откатиться» к предыдущему значению суммы, т.е. максимальному значению суммы, еще остающейся меньше 12. Предлагаем следующий вариант. PROGRAM Prim120; VAR A, S: REAL; N: INTEGER; BEGIN S:=0; N:=0; А:=7; WHILE S<12 DO
BEGIN N:=N+1; A:=A/N; S:=S+A; END; WRITELN(‘Максимальная сумма <12= ‘, S-A); WRITELN(‘Последнее слагаемое ‘,A*N,’ и его номер ’, N-1); END.
Пример 1.21. В числовую переменную последовательно вводятся отличные от нуля целые числа. Количество чисел заранее неизвестно. Определить и вывести на экран, какие (четные или нечетные) числа были введены последними и какова их сумма. Решение. В данном условии задачи обратите внимание на фразу «количество чисел заранее неизвестно». Это означает, что количество вводимых чисел может быть определено (подсчитано) только при завершении их ввода, а до начала ввода данных сведения об их количестве просто отсутствуют. Кроме того, при составлении данной программы должны быть задействованы два счетчика сумм подряд идущих четных и нечетных чисел, которые при отсутствии подсчитываемых значений должны обнуляться. Возможный вариант программы. PROGRAM Prim121; VAR S1, S2, X: INTEGER; {S1- сумма подряд идущих нечетных чисел, S2 - сумма подряд идущих четных чисел, Х - переменная, содержащая введенное число} BEGIN S1:=0; S2:=0; WRITE(‘Введите число ‘); READLN(Х); WHILE X<>0 DO BEGIN IF X MOD 2<>0 THEN BEGIN S1:=S1+X; S2:=0 END ELSE BEGIN S2:=S2+X; S1:=0 END; WRITE(‘Введите число’); READLN(X); END; IF S1<>0 THEN WRITELN('Последними были введены нечетные числа. Их сумма = ‘, S1); IF S2<>0 THEN WRITELN(‘Последними были введены четные числа. Их сумма =’, S2); END.
Пример 1.22. Найти сумму и количество цифр натурального числа N. Решение. Обозначим: S - сумма цифр числа; К - количество цифр числа; Z - выделенная цифра числа; СН - целое частное от деления. Предложенный алгоритм базируется на выделении всех цифр числа, начиная с младшего разряда, методом последовательного деления и получения целых частных на основании данной системы счисления до тех пор, пока целое частное от деления не станет равным нулю. Текст программы PROGRAM Prim122; VAR S, K, Z, CH: INTEGER; N: 1.. MAXINT; BEGIN WRITE(‘Введите натуральное число ‘); READLN(N); S:=0; K:=0; CH:=N; WHILE CH<>0 DO BEGIN K:=K+1; Z:=CH MOD 10; S:=S+Z; CH:=CH DIV 10; END; WRITELN(‘Количество ‘,K,’ и сумма цифр ‘, S) END.
Пример 1.23. В числовую переменную вводится число в десятичной системе счисления, не превышающее по модулю 10000. Необходимо вывести на экран представление этого числа в двоичной системе счисления. Решение. Обозначим объекты программы: N - целое число; К - количество цифр двоичного числа; Z(14) - массив с цифрами двоичного числа; CН - целое частное. Перевод десятичного числа в двоичную систему счисления можно описать следующей последовательностью шагов: 1. Последовательно делим данное число и получаемые целые частные на 2 до тех пор, пока последнее частное не станет равным нулю. 2. Запоминаем все остатки от деления данного числа и целых частных на 2. 3. Составляем число в двоичной системе счисления, начиная с последнего остатка и кончая первым. Для запоминания остатков от деления надо организовать в памяти одномерный массив. Но какой размерности? По условию, целое десятичное число не должно превышать 10000, т.е. 1000010 =271016 =10 0111 0001 00002. Отсюда видно, что максимальное количество значащих разрядов двоичного числа не может превышать 14. Эта величина и будет определять размерность одномерного массива.
При выводе изображения двоичного числа анализируется его знак, т.к. в условии задачи ничего не сказано о том, какие числа переводятся - положительные или отрицательные. Вариант программы Program Prim123; Var Z: Array[1..14] of Integer; N, I, K, CH: Integer; S,q: Real; Begin Write(‘Введите целое число ‘); Readln(N); K:=0; CH:=ABS(N); WHILE CH<>0 Do Begin K:=K+1; Z[K]:=CH MOD 2; CH:=CH DIV 2; End; Writeln(‘Число ’,N,’ в двоичной системе счисления’); If N<0 THEN Write(‘-‘); q:=1; S:=0; For I:=1 TO K DO Begin S:=S+Z [I]*q; q:=q*10; End; Writeln(S:14:0); End. Контрольные вопросы 1. Что такое цикл? 2. Какие действия необходимо выполнить для организации цикла? 3. Что такое итерационный циклический процесс? 4. Какие операторы цикла имеются в Турбо Паскале? 5. Какие средства языка целесообразно использовать для организации циклов с заданным числом повторений? 6. Как работает оператор цикла While? 7. В чем заключается различие между операторами Repeat и While? 8. Каково может быть условие выхода из цикла при вычислении значения суммы бесконечного ряда? 9. Зачем используются рекуррентные соотношения для вычисления значений члена ряда?
Задачи I уровня
Определить, какой цикл (по счетчику или по условию) требуется в задаче. Для цикла по условию определить, где должна производиться проверка условия выхода из цикла (в начале или в конце тела цикла) и, исходя из этого, использовать соответствующие операторы цикла. 1. Вычислить 1 + 1/2 + 1/3 +... + 1/10. 2. Вычислить 5 + 8 + 11 +... + 35. 3. Вычислить 1 + 3 + З2 +... + 37. 4. Вычислить 1/2 + 1/22 +... + 1/210. 5. Вычислить 2/3 + 3/4 +... + 10/11. 6. Вычислить 2 + 23 +... + 210. 7. Вычислить у = 1/2 + 2 х 3 при х = -5, -4.5, - 4,..., 3. 8. Составить таблицу стоимости порций сыра весом 50, 100,..., 1000 г (цена 1 кг сыра 80 руб.). В задачах № 9-15 вычислитьсумму заданного числа членов знакопеременного ряда. 9. S = 10. S = 11. S = 0.3 12. S = 2 + 13. S = 1 + 14. S = 15. S = 0.4 Задачи II уровня 1. Имеется последовательность ненулевых целых чисел, за которой следует 0. Определять, сколько раз в последовательности меняется знак чисел. 2. Составить программу для вычисления значения: у=х + х3/ 3! + х5/ 5! + х7/ 7!+...,учитывая, что Расчет продолжать до тех пор, пока модуль разности между очередным и предыдущим значениями у будет больше заданной величины (точности вычислений). 3. Имеется последовательность положительных и отрицательных чисел. Определить, является ли последовательность чисел, находящихся до первого отрицательного числа, возрастающей. 4. Имеется шестизначный номер лотерейного билета. Определить является ли номер «счастливым», т.е. равны ли суммы первых и последних трех цифр. 5. Имеется последовательность вещественных чисел, содержащая нулевые значения. Определить, сколько чисел, расположенных до первого нулевого значения, больше своих «соседей». 6. Перед паромной переправой остановились легковые и грузовые автомобили. Определить, сколько легковых автомобилей находится в начале очереди. 7. На шоссе образовалась «пробка» из легковых и грузовых автомобилей. Определить, сколько грузовых автомобилей находится между легковыми. 8. Вычислить сумму ряда 9. Вывести на экран N чисел Фибоначчи (N задается из диапазона от 2 до 21), значения частных от деления каждого из этих чисел на предыдущее число и сумму этих частных. Числа Фибоначчи - это такая последовательность целых чисел, в которой два первых числа равны 1, а каждое следующее число равно сумме двух предыдущих. (Числа Фибоначчи: 1, 1, 2, 3, 5, 8,...). 10. В числовые переменные вводятся два натуральных числа Х и N. Необходимо найти ближайшее к Х и превосходящее его натуральное число, кратное N, а также сумму его цифр. Выдать на экран соответствующие сообщения. 11. Найти минимальное количество слагаемых в сумме членов ряда 1·1 + 1·2·2 + 1·2·3·3 + 1·2·3·4·4 + ···, при котором эта сумма станет больше 120. Кроме этого вывести на экран значение последнего слагаемого и его номер. 12. Не используя массивы, ввести экзаменационные оценки N учеников по К предметам (N и К задаются). Определить и вывести на экран количество учеников, не получивших: а) ни одной "пятерки"; б) ни одной оценки выше "тройки". 13. В числовую переменную последовательно вводятся отличные от нуля целые числа. Количество чисел заранее неизвестно. Определить и вывести на экран, какие (четные или нечетные) числа были введены последними и какова их сумма. 14. Ввести с клавиатуры границы диапазона трехзначных натуральных чисел, из которых необходимо напечатать только простые. Определить количество таких чисел и их сумму. 15. Найти максимальное количество слагаемых в сумме членов ряда 16. Вычислить последнюю сумму членов ряда 17. В числовую переменную последовательно вводятся отличные от нуля целые числа. Количество чисел заранее неизвестно. Определить и вывести на экран, какие (положительные или отрицательные) числа были введены последними и какова их сумма. 18. Вычислить сумму ряда 2 + 4 + 8 + 16 + 32 + ···. Суммирование осуществлять, пока разность между текущим и предыдущим членами остается меньше 200. Кроме суммы вывести на экран значение последнего слагаемого и его номер. 19. В числовую переменную последовательно вводятся произвольные числа, не равные нулю. Количество вводимых чисел заранее неизвестно. Определить порядковые номера и значения первого из максимальных и последнего из минимальных чисел этой последовательности, а также произведение двух этих чисел. 20. Вычислить сумму членов ряда
чениями суммы остается больше 0,001. Кроме этого найти значение последнего слагаемого и его номер. 21. В числовую переменную последовательно вводятся ненулевые целые числа. Количество вводимых чисел заранее неизвестно. Необходимо определить максимальную длину цепочки из подряд идущих положительных чисел и максимальную длину цепочки из подряд идущих отрицательных чисел. 22. В числовую переменную в произвольном порядке последовательно вводятся нулевые и положительные числа. Количество вводимых чисел заранее неизвестно. Определить сумму и количество введенных положительных чисел, а также максимальное количество подряд введенных нулевых чисел. 23. В числовую переменную последовательно вводятся произвольные числа, не равные нулю. Количество вводимых чисел заранее неизвестно. Требуется вычислить и напечатать сумму тех из них, порядковые номера которых являются простыми числами. 24. В числовую переменную последовательно вводятся целые числа, не равные нулю. Количество вводимых чисел заранее неизвестно. Требуется найти сумму тех введенных чисел, в которых встречаются две цифры 5. 25. В числовую переменную последовательно вводятся ежедневные замеры дневных температур осенних и зимних дней. Количество вводимых замеров заранее неизвестно. Определить количество дней с температурой ниже чем минус 5 градусов, а также максимальное количество подряд идущих дней с нулевой температурой. 26. В одну и ту же переменную х вводятся вещественные числа по модулю больше 1 и меньше 2. Количество вводимых чисел заранее неизвестно. Для каждого значения х вывести на экран сумму ряда 1 + х + х /2 + х /3 + + х /5 + х /8 + х /13 + х /21 +......, значение последнего слагаемого и его порядковый номер. Суммирование выполнять до тех пор, пока модуль разности между текущим и предыдущим членами остается больше 0.0001.
Глава 2. СТРУКТУРИЗАЦИЯ ПРОГРАММНЫХ ДАННЫХ
2.1. Массивы
Задачи, решаемые на ЭВМ, являются математическими моделями процессов или явлений реальной жизни. В математической модели находят отражение наиболее существенные связи между реальными объектами. Модели реальных объектов вместе с присущими им связями образуют структуры данных, процесс обработки которых и описывается с помощью алгоритмов. Разные классы решаемых на ЭВМ задач характеризуются и разными структурами данных, что находит отражение и в соответствующих языках программирования. Рассмотрим наиболее часто используемые структуры данных языка Турбо Паскаль. Необходимость в массивах возникает всякий раз, когда при решении задачи приходится иметь дело с большим, но конечным количеством однотипных упорядоченных данных. Допустим, что требуется вычислить значение многочлена Р (объект задачи): Р = а + bх + сx2 + dx3 + ех4 + fx5, где a, b, c, d,e, f — коэффициенты многочлена (объекты задачи арифметического типа). В алгоритме это переменные и их количество (шесть) определено в постановке задачи, т.е. к моменту разработки алгоритма. Удобно такие разрозненные переменные объединить в совокупность — массив, именуяих затем общим именем (именем массива) и индексами (номерами в массиве). В рассматриваемом примере введем массив А с шестью элементами (а 1— а 6): Р = а 1 + а 2 х + а 3 а 2 + а 4 х 3 + а 5 х 4+ а 6 х 5. Массив А представляет собой одномерный массив, так как для индексации его элементов используется один индекс. В задачах используются не только одномерные, но и многомерные массивы, в частности двумерные. Для индексации элементов двумерного массива указываются два индекса — номер строки и номер столбца. Для наглядности такой массив представляется в виде матрицы, состоящей из m строк и n столбцов. Например, оценки трех учеников по четырем предметам можно представить массивом Х из 3 строк и 4 столбцов: Х 11 X 12 Х 13 X 14 X 21 X 22 Х 23 Х 24 Х 31 Х 32 Х 33 Х 34 При этом одномерные массивы часто называют векторами, а двумерные - матрицами. Массиву дается имя и указывается его размер. Итак, массив - это поименованный упорядоченный набор фиксированного количества некоторых однотипных значений (компонент массива). Имя всего массива называют полной переменной, поскольку ее значение есть весь массив. К каждой компоненте массива имеется прямой доступ. Для этого после имени массива следует указать в квадратных скобках индекс компоненты, например Х[10], MATR[4,5]. Такие переменные называются переменными с индексом, или индексными переменными. Значением такой переменной является не весь массив, а отдельная компонента, номер которой задается индексом. Поэтому переменную с индексом называют еще частичной переменной. Отметим, что в двумерном массиве первый индекс указывает номер строки, а второй - номер столбца. В общем случае в качестве индекса может быть использована не только константа, но и выражение, значение которого и определяет номер компоненты массива. При этом важно, что в индексное выражение могут входить переменные, так что при изменении их значений меняется и значение индекса, которое определяет номер компоненты массива, например А[К]; А[I + J]; X[1,J]; X[I + 2J]. Таким образом, одна и та же переменная с индексом в процессе выполнения программы может обозначать различные компоненты массива. Очень важно в таких случаях помнить, что переменные, используемые для индексации, к моменту обработки элементов массивов должны быть определены. Возможны не только арифметические массивы, но массивы других типов, в частности строковые. Например, список фамилий (объект задачи) можно рассматривать как одномерный строковый массив.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 3828; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.86.13 (0.015 с.) |

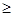 Е.
Е. при х =0,5.
при х =0,5.
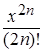 будем вычислять по рекуррентной формуле, выражая последующий член через предыдущий:
будем вычислять по рекуррентной формуле, выражая последующий член через предыдущий: .
. . Суммирование осуществлять, пока разность между предыдущим и текущим членами остается больше 0,04. Кроме суммы вывести на экран значение последнего слагаемого и его номер.
. Суммирование осуществлять, пока разность между предыдущим и текущим членами остается больше 0,04. Кроме суммы вывести на экран значение последнего слагаемого и его номер. , при котором эта сумма остается меньше 12. Кроме этого вывести на экран значение последнего слагаемого и его номер.
, при котором эта сумма остается меньше 12. Кроме этого вывести на экран значение последнего слагаемого и его номер. ,
,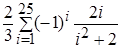
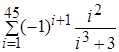
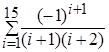
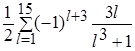

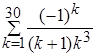
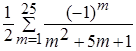
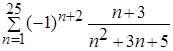
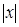 < 1.
< 1. . Суммирование осуществлять, пока разность между предыдущим и текущим членами остается больше 0.04. Кроме суммы вывести на экран значение последнего слагаемого и его номер.
. Суммирование осуществлять, пока разность между предыдущим и текущим членами остается больше 0.04. Кроме суммы вывести на экран значение последнего слагаемого и его номер.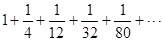 , при которой разность между предыдущим и текущим членами ряда остается больше 0.007. Кроме суммы вывести на экран значение последнего слагаемого и его номер.
, при которой разность между предыдущим и текущим членами ряда остается больше 0.007. Кроме суммы вывести на экран значение последнего слагаемого и его номер. . Суммирование осуществлять, пока разность между текущим и предыдущим зна-
. Суммирование осуществлять, пока разность между текущим и предыдущим зна-


