
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реализация циклических алгоритмовСодержание книги Поиск на нашем сайте
Циклические алгоритмы Часто при решении задач приходится многократно выполнять одни и те же действия при различных значениях входящих в них величин. Такие многократно повторяющиеся участки вычислительного процесса называются циклами. Соответственно циклический алгоритм — это алгоритм, содержащий циклы. Использование циклов позволяет существенно сократить схему алгоритма и длину соответствующей ему программы. Для организации любого цикла необходимы блоки, выполняющие следующие функции: 1. Задание начального значения переменной, изменяющейся в цикле. 2. Изменение переменной перед каждым новым повторением цикла. 3. Проверку условия окончания цикла и выход из него, если цикл закончен. 4. Переход к началу цикла, если цикл не закончен. Отметим, что возможен «досрочный» выход из цикла с помощью условного оператора и оператора перехода, а также процедур Break или Exit. Различают два типа циклов: циклы с известным числом повторений (арифметические) и циклы с неизвестным числом повторений (итерационные). Подчеркнем, что число повторений определяется на момент разработки алгоритма. Цикл, содержащий внутри себя один или несколько других циклов, называется вложенным. Цикл, охватывающий другие циклы, называется внешним, а остальные - внутренними. Правила организации для внешних и внутренних циклов такие же, как и для простого цикла. Параметры этих циклов изменяются не одновременно: при одном значении параметра внешнего цикла параметр внутреннего цикла принимает по очереди все свои значения. В качестве параметров для этих циклов должны использоваться переменные с разными именами.
Реализация циклических алгоритмов Для реализации циклов в программах на языке Турбо Паскаль можно использовать условные операторы в сочетании с оператором перехода, но наибольший эффект дают специальные операторы— операторы циклов. Прежде всего рассмотрим циклы с заданным (известным) числом повторений.
Цикл с известным числом повторений Цикл с известным числом повторений в Турбо Паскаль называется также циклом с параметром. Общая форма конструкции, образующей цикл, имеет вид: - при увеличении значения параметра FOR <переменная> = Выр.1 ТО Выр.2 <оператор>
- при уменьшении значения параметра FOR <переменная> = Выр.1 DOWNТО Выр.2 <оператор> Здесь FOR (для), ТО (до), DOWNТО — ключевые слова языка Турбо Паскаль. <Переменная> называется параметром цикла, или управляющей переменной цикла. В качестве нее можно использовать любую переменную порядкового типа. Выр.1, Выр. 2 — выражения, определяющие соответственно начальное и конечное значения параметра цикла. Они могут быть записаны константами или выражениями, совпадающими по типу с параметром цикла. Выр.1, Выр.2 вычисляются до входа в тело цикла. Первая строка конструкции (оператор FOR) обычно называется заголовком цикла. Оператор, следующий за ним, образует тело цикла. Это может быть любой исполнимый оператор языка, в том числе и составной.
Примеры реализации циклического алгоритма Пример 1.10. Разработать программу для вычисления суммы К членов ряда, определяемых общей формулой C i = (-1) i +1 Решение. Анализ постановки задачи В формуле для членов ряда символом «!» обозначена функция, называемая факториалом и определяемая в виде: К!=1∙2∙3∙...∙ К. Исходными данными для решения задачи, очевидно, являются число членов ряда K и значение аргумента Х. Обозначим вычисляемую сумму через S, счетчик ряда — I, очередной член ряда — С. Вычисление суммы ряда — это цикл с известным (заданным) числом повторений (от 1 до К), в котором не только вычисляются текущие значения членов ряда, но и накапливается их сумма путем прибавления полученного значения члена ряда к сумме предыдущих. В нашем примере формулой для накопления суммы нескольких слагаемых является формула Si:= Si -1 + Сi. Таким образом, значению суммы на i -м шаге присваивается значение частичной суммы на предыдущем шаге плюс слагаемое Сi. Поскольку надобности в запоминании значений всех промежуточных сумм и членов ряда нет, в качестве S нужно использовать простую переменную и накопление суммы вести по формуле S:= S + С. До ввода в цикл вычисления суммы S его надо подготовить, т.е. присвоить S нулевое значение (“обнулить”) — S = 0, а перед накапливанием вычислить очередное слагаемое С — очередной член ряда. Будет совершенно нерационально использовать для вычисления очередного члена ряда общую формулу, указанную в постановке задачи. Действительно, например, для 5-го номера получим:
C 5 = + Отсюда следует, что для вычисления очередного слагаемого можно использовать оператор присваивания: C:= - С * I / X. Начальное значение переменной С надо определить до входа в цикл: С = -1. После выхода из цикла необходимо вывести полученные результаты. Форма вывода результатов в постановке задачи не определена, выбираем ее сами, например, в виде: Результаты вычислений Число членов ряда: * * * Аргумент ряда: **.** Сумма ряда: ****.*** Этот макет реализуется необходимой последовательностью операторов вывода. Таким образом мы достаточно детализировали алгоритм решения задачи. Текст программы PROGRAM Prim110; {Вычисление суммы ряда } VAR X, C, S: REAL; K, I: INTEGER; {К—число членов ряда } {X — аргумент } {С—очередной член ряда } {I—номер члена ряда } {S - вычисляется сумма } BEGIN {Этап ввода исходных данных } WRITE(‘Число членов ряда-‘); READLN(К); WRITE(‘Аргумент (больше 0)'); READLN(Х); {Этап вычислений } {Подготовка цикла} S:=0; C:= -1; FOR I:=1 TO K DO BEGIN {Вычисление значения члена ряда} С:= -C*I/X; {Накопление суммы} S:=S+C; END; {Этап вывода } WRITELN(‘Результаты вычислений'); WRITELN(‘Число членов ряда: ‘,К:3); WRITELN(‘Аргумент ряда: ‘, Х:5:2); WRITELN(‘Сумма ряда: ‘, S:7:3); END. Формальное исполнение программы Принимаем К =4. Значение аргумента можно не конкретизировать, записывая каждый раз выражение для вычисления слагаемого. Результаты формального исполнения: Подготовка: S = 0, С = -1 i = l c = +l/ x, s = + l/ x; i = 2 c = -l · 2/ x 2, s = +l / x – l · 2/ x 2; i = 3 с = +1 · 2 · 3/ х 3, s = +l/ x – l · 2/ x 2 + 1 · 2 · 3/ x 3; i = 4 с = -1 · 2 · 3 · 4/ х 4, s = +1 /x – 1 · 2/ х 2 + 1 · 2 · 3/ х 3 – 1 · 2 · 3 · 4/ x 4. Результаты, полученные при формальном исполнении программы, свидетельствуют о правильности составленного алгоритма. Пример 1.11. Вычислить факториал p= n!, (n! = 1 · 2 · 3 … n) при n = 6. Решение. Вариант программы будет иметь вид: PROGRAM Prim111; VAR N, P, I: INTEGER; BEGIN N:=6; P:=1; For I:=1 TO N DO P: = P*I; WRITELN(‘P=’,P) End.
Пример 1.12. Найти и напечатать все делители натурального числа N. Решение. Перед составлением программ по обработке целых чисел необходимо ознакомиться с арифметическими операциями DIV и MOD. Напомним, что операция DIV является операцией целочисленного деления и выделяет целую часть от деления одного целого числа на другое. Операция MOD выделяет остаток от деления одного целого числа на другое. Например: А:=5 DIV 2; WRITE(A); На экране появится «2». М:=5 MOD 2; WRITE(M); На экране появится «1». Если даны 2 числа А и В, то по определению В является делителем числа А, если А делится на В без остатка. Минимальное количество делителей у каждого целого числа равно двум — это единица и само число. Число, имеющее только два делителя, называется простым. В данном алгоритме делители определяются перебором всех чисел в диапазоне от 2 до N/2. Если заданное число N делится без остатка на какое-либо из этих чисел, то это число будет являться одним из делителей числа N. Диапазон делителей ограничен сверху величиной N/2, так как ни одно число не делится без остатка на число, большее своей половины. Вариант программы PROGRAM Prim112; TYPE NATUR = 1.. MAXINT; VAR N: NATUR; I: INTEGER; BEGIN WRITE(‘Введите число‘); READLN(N); WRITELN(‘Делители числа’,N, ‘:'); WRITE(1); FOR I:=2 TO N DIV 2 DO IF N MOD I = 0 THEN WRITE(I:5); WRITELN(N); END. В приведенной программе делители только выводятся на экран, но не запоминаются. В ряде случаев необходимо запоминать делители в оперативной памяти. Для этого создается одномерный массив, имеющий размерность, достаточную для запоминания всех делителей числа.
Пример 1.13. Ввести с клавиатуры границы диапазона трехзначных натуральных чисел, из которых напечатать только простые. Определить количество таких чисел и их сумму. Решение. Обозначим: А - нижняя граница диапазона; В - верхняя граница диапазона; S - сумма простых чисел; KOL - количество простых чисел; FL - признак простого числа (0 - простое число, 1 - непростое). В приведенном алгоритме простые числа определяются перебором всех чисел данного диапазона и вычислением делителя каждогоиз них (во вложенном цикле FOR I:=...). Если у числа только два делителя (единица и само число), то число простое (FL=0), если больше, то число непростое (FL=1). Вариант программы PROGRAM Prim113; VAR A, B, N: 100..999; FL, D, S, KOL: INTEGER; BEGIN WRITE(‘Нижняя и верхняя границы диапазона трехзначных чисел‘); READLN(А, В); S:=0; KOL:=0; FOR N:=A TO В DO BEGIN FL:=0; FOR D:=2 TO N DIV 2 DO IF N MOD D=0 THEN BEGIN FL:=1; BREAK END; IF FL=0 THEN BEGIN KOL:=KOL+1; S:=S+N END; END; WRITELN(‘Сумма ‘,S,’ и количество простых чисел ’, KOL) END.
Задача 1.14. В произвольной последовательности N вещественных чисел определить максимальное количество подряд идущих нулей. Решение. Обозначим объекты задачи: N - количество чисел последовательности, S - счетчик подряд идущих нулей, МАХ - максимальное количество подряд идущих нулей, Х - переменная с очередным числом последовательности. Возможный вариант программы PROGRAM Prim114; VAR N, I, S, MAX: INTEGER; X: REAL; BEGIN WRITE(‘Количество чисел в последовательности’); READLN(N); S:=0; МАХ:=0; FOR I:=1 ТО N DO BEGIN WRITE(‘Значение ‘, I:4, ‘-го числа последовательности ’); READLN(X); IF Х=0 THEN S:=S+1 ELSE S:=0; IF S > MAX THEN MAX:=S END; WRITELN(‘Максимальное количество подряд идущих нулей = ', МАХ:4); END.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 1536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.118.82 (0.009 с.) |

 для аргумента х > 0.
для аргумента х > 0.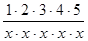 , а для шестого – С 6 = -
, а для шестого – С 6 = -  .
.


