
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение емкости конденсатора.Содержание книги
Поиск на нашем сайте
Определение активного сопротивления и индуктивности катушки. Собрать схему (Рис. 4), выставить напряжение источника переменного тока U 0 @ 10 В. Используя показания амперметра и ваттметра
а по закону Ома – полное сопротивление катушки, включающее в себя и активную, и реактивную составляющие:  . .
Исходя из
Проверка закона Ома для переменного тока. По полученным значениям индуктивности и емкости и выбранном значении активного сопротивления R порядка 500 Ом рассчитать величину тока, который должен протекать в цепи при напряжении источника переменного тока U = 10 В:
где R 0 включает в себя активные сопротивления магазина сопротивлений, катушки и амперметра
Изучение резонанса напряжений в цепи переменного тока. Зная индуктивность катушки и емкость конденсатора, входящих в последовательный контур, рассчитать резонансную частоту:
Вопросы к зачету по работе. – Что такое переменный ток, и какие параметры характеризуют переменный ток? – Как определяется напряжение переменного тока в цепи, содержащей резистор, конденсатор и катушку индуктивности? – Объяснить вид векторной диаграммы, характеризующей соотношение фаз напряжений на активных и реактивных элементах цепи. – Как рассчитывается полное сопротивление электрической цепи переменного тока, содержащей резистор, конденсатор и катушку индуктивности? – Что такое резонанс напряжений, и при каком условии он возникает в последовательной цепи переменного тока? – От чего зависит соотношение напряжений на активном и реактивных элементах цепи?
Лабораторная работа № 11 Изучение явления термоэлектронной эмиссии Цель работы. Изучение условий и закономерностей протекания тока в вакууме на примере явления термоэлектронной эмиссии. Знания, необходимые для допуска к работе. – Понятие "электронного газа" в металлах; – Условия протекания тока в вакууме; – Закон Богуславского-Ленгмюра. Краткие сведения из теории. Протекание тока в вакууме можно рассмотреть на примере вакуумной двухэлектродной лампы (вакуумного диода). Она представляет собой герметично запаянную стеклянную колбу, из которой откачан воздух, с двумя электродами (Рис. 1). Для того, чтобы через вакуум протекал электрический ток, необходимо электрическое поле и наличие свободных носителей заряда в промежутке между электродами. Понятно, что в вакууме практически нет носителей, поэтому нужно каким-либо способом внести некоторое количество заряженных частиц в вакуумный промежуток. возвращающие электроны в металл. Металл окружен "облаком", состоящим из электронов.
 Рассмотрим один из способов – термоэлектронную эмиссию. Это явление испускания электронов металлом при нагревании. Если собрать цепь, содержащую вакуумный диод, источник напряжения и амперметр (Рис. 3), то при холодном отрицательном электроде (катоде) амперметр показывает нуль при подаче напряжения на положительный электрод (анод). Если нагреть катод, подключив к нему дополнительный источник напряжения, амперметр обнаружит появление тока. Зависимость анодного тока от напряжения между анодом и катодом нелинейная, т.е. при протекании тока в вакууме закон Ома не выполняется. Даже при отсутствии разности потенциалов амперметр регистрирует ток, так как часть электронов, покинувших катод, движется в сторону анода и может его достичь. При увеличении напряжения таких электронов становится все больше, и при некотором напряжении наступает насыщение (сколько электронов в единицу времени покидает катод, столько же достигает анода). Ясно, что чем больше температура катода, тем больше электронов вылетает из него, и, соответственно, тем выше ток насыщения. Зависимость тока от напряжения в области нарастания тока имеет вид: Рассмотрим один из способов – термоэлектронную эмиссию. Это явление испускания электронов металлом при нагревании. Если собрать цепь, содержащую вакуумный диод, источник напряжения и амперметр (Рис. 3), то при холодном отрицательном электроде (катоде) амперметр показывает нуль при подаче напряжения на положительный электрод (анод). Если нагреть катод, подключив к нему дополнительный источник напряжения, амперметр обнаружит появление тока. Зависимость анодного тока от напряжения между анодом и катодом нелинейная, т.е. при протекании тока в вакууме закон Ома не выполняется. Даже при отсутствии разности потенциалов амперметр регистрирует ток, так как часть электронов, покинувших катод, движется в сторону анода и может его достичь. При увеличении напряжения таких электронов становится все больше, и при некотором напряжении наступает насыщение (сколько электронов в единицу времени покидает катод, столько же достигает анода). Ясно, что чем больше температура катода, тем больше электронов вылетает из него, и, соответственно, тем выше ток насыщения. Зависимость тока от напряжения в области нарастания тока имеет вид:
где C – постоянная, зависящая от формы и размеров электродов. Например для плоских электродов с площадью S и расстоянием между ними d
Формула зависимости тока от напряжения носит название закона Богуславского-Ленгмюра или "закона
где
Работа выхода электронов из металла также является одной из важнейших характеристик эмиссионных свойств металлов. Практические задания
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 495; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 Собрать схему (Рис. 3), выставить напряжение источника переменного тока ВС-24 U = 10 В и рассчитать емкость конденсатора, зная, что частота промышленного тока n = 50 Гц:
Собрать схему (Рис. 3), выставить напряжение источника переменного тока ВС-24 U = 10 В и рассчитать емкость конденсатора, зная, что частота промышленного тока n = 50 Гц: .
. рассчитать активное сопротивление:
рассчитать активное сопротивление: ,
, получаем формулу для расчета индуктивности катушки:
получаем формулу для расчета индуктивности катушки: .
. ,
, .
. Собрать схему, приведенную на (Рис. 5), и убедиться, что экспериментально измеренный ток соответствует расчетному. Тем самым будет подтверждена выполнимость закона Ома для переменного тока.
Собрать схему, приведенную на (Рис. 5), и убедиться, что экспериментально измеренный ток соответствует расчетному. Тем самым будет подтверждена выполнимость закона Ома для переменного тока. .
. Построить и проанализировать зависимости
Построить и проанализировать зависимости  ,
,  ,
, 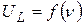 ,
,  и
и  .
. Потенциальные энергии электронов иллюстрирует энергетическая диаграмма (Рис. 2). Уровень W 0 соответствует энергии покоящегося электрона вне металла, Eс – наименьшая энергия электронов проводимости (дно зоны проводимости). Распределение потенциальной энергии имеет вид потенциальной ямы, глубина которой
Потенциальные энергии электронов иллюстрирует энергетическая диаграмма (Рис. 2). Уровень W 0 соответствует энергии покоящегося электрона вне металла, Eс – наименьшая энергия электронов проводимости (дно зоны проводимости). Распределение потенциальной энергии имеет вид потенциальной ямы, глубина которой  называется электронным сродством и является важной характеристикой вещества. Понятно, что если электрон имеет полную энергию W меньше W 0, то он не может покинуть металл. Для этого ему нужно сообщить дополнительную энергию, и в зависимости от способа сообщения этой энергии явление выхода электронов из металла называется термоэлектронной (при нагревании), фотоэлектронной (под воздействием света), вторичной электронной (в результате бомбардировки другими частицами) эмиссией.
называется электронным сродством и является важной характеристикой вещества. Понятно, что если электрон имеет полную энергию W меньше W 0, то он не может покинуть металл. Для этого ему нужно сообщить дополнительную энергию, и в зависимости от способа сообщения этой энергии явление выхода электронов из металла называется термоэлектронной (при нагревании), фотоэлектронной (под воздействием света), вторичной электронной (в результате бомбардировки другими частицами) эмиссией. ,
, .
. ".
". Характер зависимости можно объясняеть следующим образом. При эмиссии электронов из катода между электродами находится созданный этими электронами объемный отрицательный заряд, плотность которого плавно уменьшается по мере приближения к аноду (Рис. 4). Этот заряд оказывает тормозящее действие на движущиеся к аноду электроны. Увеличение анодного напряжения приводит к быстрому уходу электронов от катода и, следовательно, уменьшению плотности объемного заряда, вследствие чего анодный ток увеличивается.
Характер зависимости можно объясняеть следующим образом. При эмиссии электронов из катода между электродами находится созданный этими электронами объемный отрицательный заряд, плотность которого плавно уменьшается по мере приближения к аноду (Рис. 4). Этот заряд оказывает тормозящее действие на движущиеся к аноду электроны. Увеличение анодного напряжения приводит к быстрому уходу электронов от катода и, следовательно, уменьшению плотности объемного заряда, вследствие чего анодный ток увеличивается. ,
, – плотность тока насыщения, К – постоянная, которая для всех металлов с совершенно чистой поверхностью имеет примерно одинаковые значения, А – величина, имеющая размерность энергии, называемая термоэлектронной работой выхода и равная разности между энергией покоящегося электрона в вакууме W 0 и наибольшей кинетической энергией электрона в металле (уровнем Ферми) ЕF:
– плотность тока насыщения, К – постоянная, которая для всех металлов с совершенно чистой поверхностью имеет примерно одинаковые значения, А – величина, имеющая размерность энергии, называемая термоэлектронной работой выхода и равная разности между энергией покоящегося электрона в вакууме W 0 и наибольшей кинетической энергией электрона в металле (уровнем Ферми) ЕF: .
.


