
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение индуктивности, активного сопротивления катушки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для колебательного контура рекомендуется выбрать катушку 220/127 от школьного трансформатора, магазин конденсаторов Р544, выставив емкость порядка 0,5 мкФ, и магазин сопротивлений Р33.
а при подключении переменного выхода – сопротивление Z равно:
Расчет параметров колебательного контура и экспериментальное получение затухающих колебаний. Задав емкость конденсатора порядка 0,1 мкФ и активное сопротивление R равное нулю, рассчитать параметры получившегося колебательного контура: частоту n (или w), коэффициент затухания b, период затухающих колебаний Т, логарифмический декремент затухания d, добротность колебательного контура Q, критическое сопротивление Rкр. Собрать схему (Рис. 5), выставив на магазине емкостей 0,1 мкФ, на магазине сопротивлений – 0 Ом. Для того, чтобы картина затухающих колебаний была постоянно видна на экране осциллографа, необходимо периодически добавлять энергию в колебательный контур подзаряжая конденсатор. В качестве периодического источника энергии используется выход пилообразного Конденсатор Сдиф и входное сопротивление осциллографа Rвх представляют из себя дифференцирующую цепь, превращающую пилообразный сигнал в импульсный (Рис. 6). При плавном нарастании напряжения конденсатор успевает заряжаться, напряжение на нем в каждый момент времени практически равно напряжению источника пилообразного сигнала, и ток в цепи отсутствует. При резком уменьшении напряжения в цепи наблюдается импульс тока разрядки конденсатора. Выходное напряжение является дифференциалом входного напряжения по времени. Подобрать Сдиф порядка 100 ¸ 1000 пФ. По полученной картине определить параметры колебательного контура и сравнить их с рассчитанными ранее. Меняя индуктивность катушки, вводя в нее сердечник, и емкость конденсатора, пронаблюдать и объяснить изменение картины затухающих колебаний. Пронаблюдать изменение картины при увеличении активного сопротивления R. Выставить на магазине сопротивлений такое R, чтобы выполнялось условие:
и убедиться, что колебания в контуре отсутствуют. Вопросы к зачету по работе. – Объяснить физический механизм электромагнитных колебаний в колебательном контуре. – Как преобразуется энергия при электромагнитных колебаниях и чему равна полная энергия? – Как влияет наличие активного сопротивления колебательного контура на электромагнитные колебания? Что такое затухающие электромагнитные колебания? – Какие параметры контура определяют характер электромагнитных колебаний в контуре? – Объяснить, почему наличие критического сопротивления в цепи препятствует возникновению электромагнитных колебаний в контуре.
Лабораторная работа № 10 Явления в цепях переменного тока Цель работы. Изучить закономерности явлений, наблюдаемых в цепях переменного тока. Знания, необходимые для допуска к работе. – Индуктивность и емкость в цепях переменного тока; – Закон Ома для переменного тока; – Резонансные явления в цепях переменного тока. Краткие сведения из теории. Переменным током называется любой ток, величина которого периодически меняется со временем. Но чаще всего под переменным током подразумевается ток, меняющийся по закону синуса (или косинуса):
где I – амплитуда тока,
но при переменном токе в цепи, содержащей емкость и индуктивность, есть некоторые отличия. Падение напряжения на резисторе колеблется по такому же закону, как и ток
и их фазы колебаний совпадают. Напряжение на обкладках конденсатора пропорционально заряду на них в каждый момент времени
а заряд можно определить как интеграл тока по времени
Тогда
Из этого выражения следуют два вывода: во-первых, колебания напряжения на конденсаторе отстают от колебаний тока на
где
В этом случае для участка цепи, содержащего катушку (т.е. источник ЭДС, включенный навстречу току) падение напряжения равно
так как помимо ЭДС самоиндукции происходит падение напряжения на сопротивлении провода r, из которого изготовлена катушка. Если предположить его малым, то
Очевидно, что колебания напряжения на катушке опережают колебания тока на
где Сопротивления R, r называются активными (или омическими), а сопротивления XL и XC – реактивными.
 . .
Видно, что колебания напряжения и тока сдвинуты по фазе друг относительно друга на j. Вынеся общий множитель – силу тока – из-под корня, получаем выражение:
где R 0 – все активное сопротивление электрической цепи. Это выражение является математической формулировкой закона Ома для переменной цепи. Общее сопротивление цепи Z и тангенс сдвига фаз между колебаниями тока и напряжения tgj определяется по формулам:
Как видно из этих формул, полное сопротивление цепи переменного тока зависит не только от величин активного сопротивления, индуктивности и емкости, но и от частоты переменного тока. При частоте близкой к нулю полное сопротивление цепи определяется емкостным сопротивлением Интересная ситуация наблюдается, когда частота переменного тока удовлетворяет условию:
 , а сдвиг фаз – нулю. Ток в этом случае приобретает максимальное значение , а сдвиг фаз – нулю. Ток в этом случае приобретает максимальное значение  . Такое состояние цепи переменного тока называется резонансом напряжений, а частота – резонансной частотой wрез. . Такое состояние цепи переменного тока называется резонансом напряжений, а частота – резонансной частотой wрез.
Интересен также факт превышения напряжения на реактивных элементах схемы выходного напряжения источника тока. Если в момент резонанса индуктивное и емкостное сопротивления больше активного сопротивления цепи Практические задания
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.32.6 (0.007 с.) |

 Определить индуктивность и активное сопротивление катушки методом амперметра и вольтметра. Для этого собрать схему, указанную на (Рис. 4). При подключении в качестве источника тока постоянного выхода ВС-24 сопротивление rL равно
Определить индуктивность и активное сопротивление катушки методом амперметра и вольтметра. Для этого собрать схему, указанную на (Рис. 4). При подключении в качестве источника тока постоянного выхода ВС-24 сопротивление rL равно ,
, ,
, .
. напряжения на правой боковой панели осциллографа. Частоту развертки осциллографа надо подобрать так, чтобы на один период развертки приходилось несколько периодов затухающих колебаний.
напряжения на правой боковой панели осциллографа. Частоту развертки осциллографа надо подобрать так, чтобы на один период развертки приходилось несколько периодов затухающих колебаний. ,
, ,
, – циклическая частота, а
– циклическая частота, а 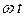 – фаза колебаний, характеризующая состояние колебательной системы в данный момент времени t.
– фаза колебаний, характеризующая состояние колебательной системы в данный момент времени t. Рассмотрим электрическую цепь, содержащую последовательно соединенные резистор, конденсатор и катушку индуктивности, подключенную к источнику переменного напряжения (Рис. 1). По этой цепи протекает ток, меняющийся по синусоидальному закону
Рассмотрим электрическую цепь, содержащую последовательно соединенные резистор, конденсатор и катушку индуктивности, подключенную к источнику переменного напряжения (Рис. 1). По этой цепи протекает ток, меняющийся по синусоидальному закону ,
, ,
, ,
, .
. .
. , а во-вторых, амплитудное значение напряжение связано с амплитудным значением тока соотношением:
, а во-вторых, амплитудное значение напряжение связано с амплитудным значением тока соотношением: ,
, называется емкостным сопротивлением.
называется емкостным сопротивлением. .
. ,
, и
и .
. ,
, – индуктивное сопротивление катушки.
– индуктивное сопротивление катушки. Соотношения фаз колебаний напряжений на активных и реактивных сопротивлениях можно проиллюстрировать на векторной диаграмме (Рис. 2). За основное направление надо взять силу тока, так как он является общим для последовательно соединенных элементов схемы. Величину амплитуды выходного напряжения можно определить, используя закон сложения векторов:
Соотношения фаз колебаний напряжений на активных и реактивных сопротивлениях можно проиллюстрировать на векторной диаграмме (Рис. 2). За основное направление надо взять силу тока, так как он является общим для последовательно соединенных элементов схемы. Величину амплитуды выходного напряжения можно определить, используя закон сложения векторов: ,
,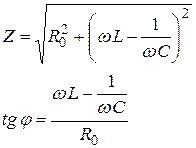 .
. и стремится к бесконечности, а сдвиг фаз
и стремится к бесконечности, а сдвиг фаз  . При высокой частоте переменного тока соответственно
. При высокой частоте переменного тока соответственно  и
и  .
. .
. , то напряжения на них
, то напряжения на них  .
.


