
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Результаты наблюдений и измерений частоты сигналаСодержание книги
Поиск на нашем сайте
методом круговой развертки
Таблица 6.13 Результаты измерения частоты и периода методом круговой развертки
6.6.6 Сопоставьте результаты, полученные в п.6.1÷6.6, сравните методы измерения по точности, удобству, производительности и экономичности измерений. Сделайте выводы по работе в целом в письменной форме в отчете.
ТРЕБОВАНИЯ К ОТЧЕТУ Отчет по лабораторной работе должен быть оформлен в соответствии с СТП НЭИС-01.07.88 и должен содержать: 1) титульный лист; 2) формулировки цели работы; 3) метрологические характеристики средств измерений, оформленные в таблицу; 4) решение задач, предложенных в методических указаниях к лабораторной работе. 5) схемы измерений по каждому пункту программы лабораторной работы, оформленные в соответствии со стандартами; 6) расчетные формулы по обработке результатов наблюдений и измерений, в том числе формулы по оценке неопределенностей измерений по каждому пункту программы лабораторной работы; 7) результаты экспериментальных исследований по каждому пункту лабораторной работы, оформленные в заготовленных таблица х в соответствии с нормативной документацией; 8) выводы по каждому эксперименту и по работе в целом.
8 МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПОДГОТОВКЕ К РАБОТЕ И ОБРАБОТКЕ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
Ознакомьтесь с методами измерения частоты и интервалов времени по литературе [1] (главы 7 и 8), [2] (главы 6 и 8), [3] (разделы 4.1-4.8) и [4]. Обратите особое внимание на изучение принципа работы цифровых частотомера и периодомера [1] (раздел 8.2), [2] (раздел 8.4), [3] (разделы 4.3 и 4.4), [4] (раздел 1.2) и применение осциллографа для измерения периода и частоты сигналов [1] (раздел 8.1), [2] (разделы 6.6, 8.2), [3] (разделы 3.6, 4.2), [5] (разделы 2.4 и 2.5). Ознакомьтесь с инструкциями по эксплуатации используемых в работе измерительных приборов [6], [7], [8] и их метрологическими характеристиками [4], [5], [8]. Оценка неопределенности измерений частоты и периода. Так как частота
то, зная оценку неопределенности одного параметра, легко оценить неопределенность другого, воспользовавшись методикой оценки неопределенности косвенных измерений [8]
или
где
Перейдя к относительным неопределенностям периода
Оценка неопределенности измерения частоты цифровым частотомером. Относительная неопределенность измерения частоты частотомером
Значение
где
Оценка неопределенности измерения периода цифровым периодомером. Относительную неопределенность измерения периода
где кварцевого) генератора частотомера;
вызванная наличием шумов в исследуемом сигнале и нестабиль- ностью порога срабатывания формирующего устройства в перио- домере;
ный на периодомере, эти импульсы иногда называют тактовыми или метками времени;
периодомере (коэффициент деления частоты исследуемого сигнала);
Значения Оценка неопределенности измерения периода методом калиброванной линейной развертки. Значение измеряемого периода
где измерение;
исследуемого сигнала. Границу относительной неопределенности измерения временного интервала
где (указана в метрологических характеристиках осциллографа);
определения уровня 0,5 пикового значения импульса (учитывается только при измерении длительности импульса);
линейного размера осциллограммы Эти границы определяют по приближенным формулам:
где
миллиметрах). Оценка неопределенности измерения частоты методом сравнения. При измерении частоты методом сравнения (рис. 8.1) путем регулировки частоты образцового генератора с помощью устройства сравнения достигают выполнения равенства
где
Рисунок 8.1. Измерение частоты методом сравнения
В этом случае относительная неопределенность измерения частоты Связь границы абсолютной неопределенности измерения частоты
или, перейдя к относительным неопределенностям, получим
С учетом неопределенности сравнения
Оценка границ неопределенности измерения частоты При этом методе происходит сравнение частот сигналов, поданных на вход
если измеряемая частота подана на вход
если исследуемый сигнал подан на вход Неопределенность частоты образцового генератора Оценка границ неопределенности измерения частоты методом синусоидальной развертки. В этом случае осуществляется сравнение частот сигналов, поданных на входы (рис. 8.2). Если фигура неподвижна, справедливо соотношение
где
горизонтальной секущей;
вертикальной секущей (см. рис. 8.2). Примечание: Секущие не должны проходить через узел. Так как этот метод является методом сравнения, то
если исследуемый сигнал подан на вход
если измеряемый сигнал подан на вход
Рисунок 8.2. Определение частоты по фигуре Лиссажу
Дальнейшая обработка аналогична разделу 8.7.
Оценка границ неопределенности измерения частоты методом круговой развертки. В этом методе сравнивают частоту сигнала
где В соответствии с разделом 8.6
если исследуемый сигнал подан на входы
если исследуемый сигнал подан на вход
ЛИТЕРАТУРА
1. Метрология, стандартизация и измерения в технике связи. Учеб. Пособие для вузов / Б.П. Хромой, А.В. Кандинов, А.Л. Сенявский и др.: Под ред. Б.П. Хромого. – М.: Радио и связь, 1986. – 424 с. 2. Ф.В. Кушнир, В.Г. Савенко, С.М. Верник. Измерения в технике связи. Учебник для вузов: 2-е изд., перераб. и доп. – М.: Связь, 1976. – 432 с. 3. Г.Я. Мирский. Электронные измерения: 4-е изд., перераб. и доп. – М.: Радио и связь, 1986. – 440 с. 4. Частотомеры Ч3-32, Ч3-33, Ч3-34 (43-34А), Ч3-36. Часть I. Методические указания по применению / П.А. Желнов, И.Н. Запасный, В.И. Сметанин, А.Г. Черевко. – Новосибирск: НЭИС, 1988. – 29 с. 5. Методические указания по применению универсальных осциллографов. Часть I / П.А. Желнов, И.Н. Запасный, В.И. Сметанин, А.Г. Черевко. – Новосибирск: НЭИС, 1989. – 37 с. 6. Частотомеры Ч3-32, Ч3-33, Ч3-34 (43-34А), Ч3-36. Часть II. Инструкции по эксплуатации / П.А. Желнов, И.Н. Запасный, В.И. Сметанин, А.Г. Черевко. – Новосибирск: НЭИС, 1988. – 37 с. 7. Оценка неопределенности измерений при экспериментальных исследованиях. Учебное пособие / И.Н. Запасный, Ю.А. Пальчун, В.И. Сметанин и др. – Новосибирск: СибГУТИ, 2001. – 60 с. 8. Н.И. Горлов, И.Н. Запасный, В.И. Сметанин. Оценка инструментальных погрешностей при экспериментальных исследованиях. Методические указания. – Новосибирск: СибГУТИ, 1995. – 27 с.
Доцент, Игорь Николаевич Запасный Доцент, Владимир Иванович Сметанин
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.107.223 (0.009 с.) |

 и период
и период 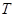 связаны соотношением
связаны соотношением , (8.1)
, (8.1)
 , (8.2)
, (8.2) , (8.3)
, (8.3) - граница абсолютной неопределенности измерения периода;
- граница абсолютной неопределенности измерения периода; - граница абсолютной неопределенности измерения частоты.
- граница абсолютной неопределенности измерения частоты. и частоты
и частоты  , получим:
, получим: . (8.4)
. (8.4) и относительной неопределенности дискретизации (квантования)
и относительной неопределенности дискретизации (квантования)  , вызванной тем, что аналоговую величину представляют целым числом импульсов
, вызванной тем, что аналоговую величину представляют целым числом импульсов 
 . (8.5)
. (8.5) , (8.6)
, (8.6) - измеренное значение частоты;
- измеренное значение частоты; - время счета, установленное на частотомере.
- время счета, установленное на частотомере. , (8.7)
, (8.7) - относительная неопределенность уровня запуска (формирования),
- относительная неопределенность уровня запуска (формирования), - период следования образцовых (счетных) импульсов, установлен-
- период следования образцовых (счетных) импульсов, установлен- - множитель периода исследуемого сигнала, установленный на
- множитель периода исследуемого сигнала, установленный на - измеренное значение периода.
- измеренное значение периода. в этом случае находят по формуле
в этом случае находят по формуле , (8.8)
, (8.8) - значение коэффициента развертки, при котором осуществляют
- значение коэффициента развертки, при котором осуществляют - размер изображения, соответствующий целому числу периодов
- размер изображения, соответствующий целому числу периодов  осциллографом, определенной по методике оценки неопределенности косвенных измерений, находят по формуле
осциллографом, определенной по методике оценки неопределенности косвенных измерений, находят по формуле , (8.9)
, (8.9) - граница относительной неопределенности коэффициента развертки
- граница относительной неопределенности коэффициента развертки - граница относительной неопределенности, вызванной неточностью
- граница относительной неопределенности, вызванной неточностью - граница относительной визуальной неопределенности измерения
- граница относительной визуальной неопределенности измерения , (8.10)
, (8.10) , (8.11)
, (8.11) - ширина линии осциллограммы (в делениях или миллиметрах);
- ширина линии осциллограммы (в делениях или миллиметрах); - размер изображения сигнала по вертикали (в тех же делениях или
- размер изображения сигнала по вертикали (в тех же делениях или , (8.12)
, (8.12) и
и  - частота измеряемого сигнала.
- частота измеряемого сигнала.
 определяется двумя компонентами: относительной неопределенностью частоты образцового источника
определяется двумя компонентами: относительной неопределенностью частоты образцового источника  и относительной неопределенностью установления равенства (8.12) – неопределенностью сравнения
и относительной неопределенностью установления равенства (8.12) – неопределенностью сравнения  .
. с границей абсолютной неопределенности частоты образцового генератора
с границей абсолютной неопределенности частоты образцового генератора  легко установить с помощью методики оценки неопределенности косвенных измерений [8]
легко установить с помощью методики оценки неопределенности косвенных измерений [8] (8.13)
(8.13) . (8.14)
. (8.14)
 . (8.15)
. (8.15) методом внешнего калибратора длительности при линейной развертке.
методом внешнего калибратора длительности при линейной развертке. и вход
и вход  осциллографа, поэтому в соответствии с формулой (8.15)
осциллографа, поэтому в соответствии с формулой (8.15) , (8.16)
, (8.16) либо
либо , (8.17)
, (8.17) .
. либо
либо  оценивают по его метрологическим характеристикам, а абсолютная неопределенность сравнения частот
оценивают по его метрологическим характеристикам, а абсолютная неопределенность сравнения частот  определяется степенью неподвижности меток на осциллограмме и составляет от сотых до десятых долей герца. Если абсолютная неопределенность образцового генератора существенно превышает (более 5 раз) абсолютную неопределенность сравнения, то последней можно пренебречь. Неопределенность измерения периода оценивают в соответствии с (8.3) и (8.4).
определяется степенью неподвижности меток на осциллограмме и составляет от сотых до десятых долей герца. Если абсолютная неопределенность образцового генератора существенно превышает (более 5 раз) абсолютную неопределенность сравнения, то последней можно пренебречь. Неопределенность измерения периода оценивают в соответствии с (8.3) и (8.4). и
и  , (8.18)
, (8.18) - частота сигнала, поданного на вход
- частота сигнала, поданного на вход  - максимальное число пересечений наблюдаемой фигуры Лиссажу с
- максимальное число пересечений наблюдаемой фигуры Лиссажу с - максимальное число пересечений наблюдаемой фигуры Лиссажу с
- максимальное число пересечений наблюдаемой фигуры Лиссажу с , (8.19)
, (8.19) , (8.20)
, (8.20)
 , поданного на вход управления яркостью луча (вход
, поданного на вход управления яркостью луча (вход  , формирующего круговую развертку. Эти частоты (при неподвижных метках) связаны соотношением
, формирующего круговую развертку. Эти частоты (при неподвижных метках) связаны соотношением , (8.21)
, (8.21) , (8.22)
, (8.22) , (8.23)
, (8.23)


