Задача 1.1. Построить нормальный сотенный поперечный масштаб

Введение

Методические указания “Решение инженерных задач на топографических картах и планах” предназначены для студентов строительных специальностей всех форм обучения при изучении дисциплины “Инженерная геодезия”.

Для выполнения задания студентам выдается ксерокопия топографической карты масштаба 1:25 000 или1:10 000 с нанесенными преподавателем исходными данными. Все построения и измерения производятся на карте, а решения выполняются на листах бумаги формата А4 и, при необходимости, дополняются графическими приложениями, которые вычерчивают в соответствии с условными знаками и шрифтами.

Студенты должны иметь: измеритель, линейку, карандаши Т, ТМ, 2М, транспортир, резинку, чертежную и миллиметровую бумагу, тушь различных цветов, чертежные перья и ручки, калькулятор.

Выполненная работа представляется на проверку преподавателю в сроки, предусмотренные календарным планом учебных занятий. При положительной оценке студентом производится защита работы.

 

1. Понятие карты и плана. Масштабы.

Для построения топографических планов поверхность Земли ортогонально проектируют на горизонтальную плоскость и уменьшают в определенное число раз. Поэтому топографическим планом называют уменьшенное и подобное изображение на бумаге отдельных небольших участков земной поверхности. Совокупность предметов местности называют ситуацией, а совокупность различных неровностей земной поверхности – рельефом. План местности, составленный без изображения рельефа, называют контурным. Например – лесоустроительный план. Таким образом, план – это чертеж, состоящий из горизонтальных проложений, полученных ортогональным проецированием соответствующих отрезков местности на горизонтальную плоскость.

Изображения больших по размерам участков земной поверхности на плоскости нельзя получить без искажений, т.е., с сохранением полного подобия. Такие участки сначала ортогонально проектируют на поверхность эллипсоида, а затем с поверхности эллипсоида по определенным математическим законам, называемым картографическими проекциями, переносят на плоскость. Таким образом, картой называют уменьшенное и закономерно искаженное изображение всей земли или отдельных частей ее поверхности на плоскости.

Степень уменьшения горизонтальных отрезков местности при перенесении их на бумагу называется масштабом плана (карты).

Масштабы бывают численные и графические. Численным масштабом называют отношение длины отрезка на карте или плане к длине соответствующей горизонтальной проекции линии на местности. Численный масштаб записывают в виде аликвотной дроби, т.е. дроби, числитель которой равен единице. Например, 1:5 000, 1:2 000, 1:25 000 и т.д. Знаменатель этой дроби показывает во сколько раз уменьшены предметы при изображении их на топографических планах, картах и профилях. На всех этих материалах подписывают численный масштаб.

Зная численный масштаб можно от единиц измерения на карте или плане переходить к единицам измерения на местности и наоборот. Например, если на карте масштаба 1:5 000 длина отрезка равна 2 см, то на местности длина его горизонтального проложения составит D=d*N=2*5000=10000 см=100м. Существенное влияние на точность измерения отрезков по любому чертежу оказывают возможности зрительного восприятия графических элементов. Невооруженный глаз человека не способен на чертеже на расстоянии 20-25 см отличить точку от отрезка, если его длина меньше 0,1 мм.

Поэтому точностью масштаба называют длину горизонтальной проекции линии местности соответствующую 0.1 мм на карте или плане. Для масштабов 1:500, 1:1 000, 1:10 000, 1:25 000 точность масштаба соответственно равна 0,05; 0,1; 1,0; 2,5 м.

Наряду с численным масштабом на практике широкое распространение получили графические масштабы,- линейный и поперечный. Пользование линейным масштабом понятно из рис.1

 

 

 

Поперечный масштаб (рис.2) применяется для более точных измерений длин линий на картах. Его гравируют на специальных металлических линейках. Точность измерения расстояния с помощью такого масштаба равна 0,5 цены наименьшего деления. С целью приобретения навыков пользования поперечным масштабом необходимо решить задачи 1 – 4.

Вопросы для самоконтроля.

1.Что называется топографическим планом?

2. Что называется топографической картой?

3. В чем отличие карты от плана?

4. Что такое масштаб?

5. Что принято за точность масштаба?

 

 

Вопросы для самоконтроля

1. Что такое номенклатура топографических карт?
2. Как по заданным географическим координатам найти номенклатуру листа карты заданного масштаба?
3. Как по номенклатуре карты определить масштаб карты?
4. Как определить номенклатуру соседних листов карты?

 

Абсциссы точек А, В,С. (км) Таблица2.

Точка	Xю.з	∆X	∆Х´	Х
А		0.356		6068.356
В		0.582	0.413	6067.585
С		0.451	0.545	6067.453

Ординаты точек А,В,С (км) Таблица 3.

Точка	Yю.з	∆Y	∆Y´	Y
А		0.296	0.702	4311.297
В		0.193		4312.193
С		0.151	0.847	4311.151

 

Вопросы для самоконтроля.

1. В чем сущность зональной системы прямоугольных координат?
2. Что принято за ось ординат и абсцисс в зональной системе координат?
3. В чем смысл преобразования ординаты?
4. Как определить номер зоны данного листа карты?
5. Какие погрешности влияют на точность измерения координат (длин линий) по карте?
6. Как определить длину отрезка, зная прямоугольные координаты его концов?
7. Чему равны искажения длин линий на осевом меридиане?
8. Как вычислить искажения длин линий в пределах зоны?
9. Как построить на карте точку по известным прямоугольным координатам?
10. Чем вызваны искажения картографических проекций?
11. Какие искажения присущи проекции Гаусса-Крюгера?

 

1. Ориентирование.

Ориентировать линию или карту – значит определить ее расположение относительно географического (истинного), осевого или магнитного меридианов.

 

Угол ориентирования, отсчитываемый от северного направления географического меридиана, называется истинным азимутом.

Трудность такого ориентирования связана с изменением величины азимута от протяженности длины линии и широты точки, в которой он измеряется. Данное обстоятельство вызвано тем, что меридианы не параллельны друг другу.

Угол между проекциями смежных меридианов на плоскости называется сближением меридианов и обозначается буквой γ и вычисляется по формуле

γ=(LA-LM) sin B, (11),

где LA и LM – долготы меридианов, проходящих через точки А и М, В – широта точки А.

Поэтомупри измерении истинного азимута линии АМ не безразлично в какой точке (А или М) производится измерение угла. Так как значения сближения меридианов изменяется, то и азимут ААМ ≠АВА+180 °. Однако, при измерении азимутов по крупномасштабным картам задача упрощается. Это связано с низкой точностью измерения углов транспортиром и малой протяженностью линии. Действительно, даже геодезическим транспортиром точность измерения угла не превышает ±15΄. А если учесть, что протяженность линии на карте масштаба 1:50 000по долготе не превышает 15΄, то для средних широт (В=55°) по формуле (11) получим γ≈12´. То есть сближение крайних меридианов карты не больше 12´, а это как видим, меньше точности измерения углов транспортиром. Для карт более крупного масштаба величина сближения меридианов в пределах данной карты будет еще меньше, а следовательно, ее можно не учитывать при измерении истинных азимутов по карте. Это позволяет производить их измерение в любой точке линии.

Задача 5.1. Измерить с помощью транспортира азимуты линий АВ, ВС, СА, ВА, СВ, АС. Вычислить румбы и внутренние углы треугольника АВС.

Для измерения азимута линии АВ необходимо провести географический меридиан, пересекающий сторону АВ треугольника (приложение 1) или продолжить сторону АВ до пересечения с меридианом, ограничивающим лист карты с запада или востока. От северного направления этого меридиана по ходу часовой стрелки транспортиром измерить искомый угол ориентирования. Результат измерения занести в таблицу 5. Точно также измерить азимуты остальных сторон. От азимутов перейти к румбам и вычислить величины внутренних углов треугольника, используя правило: угол равен разности правого и левого направлений.

Если измерения не содержат грубых погрешностей, то расхождения между значениями прямых и обратных азимутов должно быть точно 180°. Сумма внутренних углов треугольника также должна быть равна 180°. Отклонения от этих величин не должны превышать тройной точности транспортира. В качестве примера в таблице 5 приведены значения азимутов сторон треугольника АВС (приложение 1)

 

 

Таблица 5

Таблица7

Таблица 8

Рис.15 Связь между магнитными азимутами, дирекционными углами и истинными азимутами.

В табл.11 приведены результаты вычисления магнитных азимутов сторон треугольника при γ=2°20´, δ=4°15´.

 

Таблица 11.

Вопросы для самоконтроля.

1. Что называется истинным меридианом, параллелью, осевым меридианом?
2. Что означает ориентировать линию?
3. Что называется истинным азимутом, дирекционным углом, магнитным азимутом, румбом линии?
4. Какова зависимость между прямым и обратным азимутом?
5. В чем отличие сближения меридианов в проекции Гаусса-Крюгера от сближения меридианов в общем случае?
6. Что называется склонением магнитной стрелки?
7. Почему ориентирование по магнитному меридиану применяется сравнительно редко?
8. Как вычислить магнитный азимут, если известен географический азимут?
9. Как вычислить магнитный азимут, если известен дирекционный угол?

 

1. Рельеф и его изображение на картах и планах.

Совокупность неровностей земной поверхности называют рельефом. На топографических картах и планах рельеф изображают горизонталями. Горизонталь – это линия, соединяющая точки земной поверхности с одинаковыми высотами. Понятие о горизонтали можно получить, если представить себе местность, затопленную до заданной высоты непроточной водой. Береговая линия в этом случае и будет являться горизонталью. Изменяя уровень воды (высоту уровневой поверхности), получим горизонтали с различными высотами. Чтобы правильно читать рельеф необходимо знать его основные формы.

На картах и планах высоты горизонталей изменяются через равные промежутки. Разность высот соседних горизонталей называют высотой сечения рельефа, а расстояние между горизонталями на плане – заложением.

Высоту сечения рельефа выбирают в зависимости от масштаба карты или плана и характера местности. Стандартные высоты сечения рельефа: 0,25;0,5;1.0;2.0;2.5;5.0;10.0м. Горизонтали подписывают на планах и картах в разрывах основанием в сторону понижения ската местности. Кроме отметок горизонталей на картах подписывают отметки характерных точек рельефа (вершины горы, дна котловины и т.д.).

 

 

Основной характеристикой рельефа является крутизна ската. О ней можно судить по величине заложения.Чем меньше заложение (расстояние между горизонталями), тем круче скат и наоборот.

Для численной характеристики крутизны ската на местности используют угол наклона ν ° или уклон ί. Уклоном линии местности называют отношение превышения к горизонтальному проложению ί=h/d=tgν.

Из формулы следует, что уклон безразмерная величина. Его выражают или в процентах %(сотых долях), или в промилях ‰(тысячных долях), а угол наклона в градусах.

При чтении рельефа руководствуются следующими правилами:

1)бергштрихи направлены в сторону понижения;

2)основания цифр, которыми подписаны горизонтали, располагаются в направлении понижения ската;

3) к водоемам и водотокам местность понижается;

4) в одну сторону от горизонтали местность повышается, а в другую понижается;

5) горизонтали перегибаются на водораздельных линиях хребтов и тальвегах лощин

6) отметка точки на горизонтали равна отметке горизонтали;

7)отметки горизонталей всегда кратны высоте сечения рельефа.

 

Для отыскания отметки горизонтали находят ближайшую подписанную горизонталь. Отметка искомой будет равна (рис.17)

НА=Н0+nh0 (14)

где Н0 – отметка подписанной горизонтали;

n - число горизонталей между подписанной и искомой горизонталью

h0 - высота сечения рельефа.

В формуле знак (+) ставится в случае, если точка А находится выше по склону подписанной горизонтали, а (-) - если ниже. На рис.17 h0=5м, n=2 следовательно НA=210,0м. При отсутствии вблизи определяемой точки подписанной горизонтали, ее отметку находят от ближайшей подписанной отметки характерной точки. В этом случае сначала определяют отметку ближайшей горизонтали. Ее отметка будет кратна высоте сечения рельефа. Например, отметка горизонтали, расположенной ниже вершины горы с Н=216,4 равна 215,0м. От этой горизонтали, руководствуясь описанным выше методом, определяют отметку горизонтали с точкой А.

Если определяемая точка находится между горизонталями, то сначала необходимо определить отметки горизонталей, между которыми они находятся, а затем превышение между горизонталью и определяемой точкой линейным интерполированием

hc=ac h0/a, (15)

где hc - превышение между младшей горизонталью с отметкой Н 0 и точкой С;

a - заложение

ac - расстояние от младшей горизонтали до точки С.

Тогда отметка искомой точки будет равна

 

Нс=Н0+ hc (16)

Если определяемая точка лежит между горизонталями с одинаковыми отметками: перевал седловины, вершины горы или дно котловины, то отметка в этих случаях принимается равной отметке ближайшей горизонтали плюс (минус) половина высоты сечения рельефа.

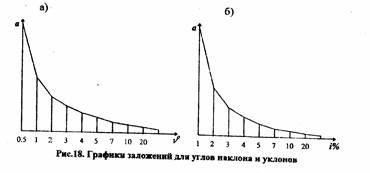
Задача 6.1.Построить масштабы заложений для значений ν° и ί,

Приведенных в таблице 12.

Графики масштабов заложений показывают зависимость между крутизной ската и величиной заложения при данной высоте сечения. Так как крутизна ската может быть выражена в градусной мере или процентах, то в соответствии с этими имеется два вида графиков, - для углов наклона и уклонов.

Если крутизна ската выражена в градусной мере, то величину заложения a вычисляют по формуле

 

a=h0ctgν (17)

а для крутизны ската, выраженной в процентах

 

a=h0100/i (18)

где h0 - высота сечения рельефа на карте, выданной для выполнения работы.

Для построения графиков необходимо вычислить заложения a при ν ° и i,

приведенных в таблице 12.

Таблица 12

 

Исходные данные для построения графиков заложений

Углы наклона	0,5°	1°	2°	3°	4°	5°	7°	10°	20°
Заложения а (м)
Уклоны %
Заложения а (м)

 

 

При построении графиков обычно по горизонтальной линии откладывают равные отрезки произвольной длины, в концах которых восстанавливают перпендикуляры, и откладывают на них в масштабе своей карты соответствующее значение из табл.12. Концы перпендикуляров соединяют плавной линией.

Таблица 13.

Крутизна ската по линии АВ

 

Н0 м	152,5	150,0	150,0	152,5	152,5	150,0	150,0	152,5	155,0
Угол наклона, ν°		2.5	0.0	2.0	0.0	0.9	0.0	1.9	1.2	1.5
Уклон, i %		4.4	0.0	3.4	0.0	1.5	0.0	3.3	2.1	2.6

 

Вопросы для самоконтроля

1. Что называется высотой (отметкой точки)?
2. Что называется горизонталью?
3. Какие формы рельефа вы знаете?
4. Как изображаются основные формы рельефа горизонталями?
5. Как вычисляется уклон (угол наклона линии)?
6. Для чего строятся графики заложений?
7. Как с помощью графиков заложений определить крутизну ската?

 

Измерение площадей

Измерить на карте площадь контура, имеющего правильную геометрическую форму (треугольник, прямоугольник и т.д.) не вызывает затруднений. Для этого достаточно измерить длину сторон фигуры и по известным формулам геометрии вычислить ее площадь.

В тех случаях, когда контур представляет собой сложный многоугольник, его площадь вычисляют путем суммирования площадей простейших геометрических фигур, на которые можно этот многоугольник разбить.

В отдельных случаях удобнее площадь многоугольника вычислять через измеренные прямоугольные координаты X и Y его вершин по формуле

 

P=1/2∑X i( Y i+1- Y i-1) (20)

или

P=1/2∑Y i( X i-1- X i+1) (21)

 

где i - номер вершины

n - число вершин

Например, для треугольника формула (20) будет иметь вид:

 

P=1/2{X4(YB-YC)+XB(YC-YA)+XC(YA-YB)} (22)

Следует иметь в виду, что если данные для вычисления площади получены из измерений по карте, то независимо, по каким формулам производится вычисление площади, этот способ будет называться графическим.

 

Задача 7.1. Вычислить площадь треугольника АВС, используя прямоугольные координаты вершин, полученные в задаче 4.1. Вычисление выполнить в табл.14

.

Таблица 14

Вычисление площади треугольника АВС

Название вершин	Хb км	Yb км	Y i+1 Y i-1	X i( Y i+1- Y i-1)
А	6068.356	4311.297	-0.896 +1.042 -0.146	-5436.437
В	6067.585	4312.193	6323.2269
С	6067.453	4311.151	-885.8674
А	6068.356	4311.297	P=0.461км²

 

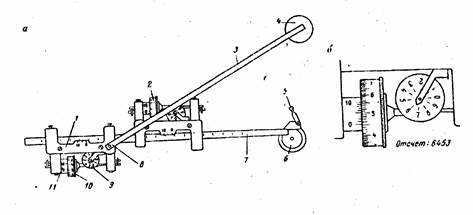
Большинство контуров на карте, особенно ландшафтного характера, имеют сложную криволинейную форму. Для измерения площади такого контура применяют или палетку или планиметр.

Палетка представляет собой сетку квадратов, прямоугольников или других правильных геометрических фигур, нанесенных на прозрачную основу.

Измерение выполняют путем подсчета числа целых фигур и их дробных частей. Зная площадь одной такой фигуры, вычисляют площадь всего контура. Палетки применяются для измерения площадей малых контуров (вкраплений). Для измерения площадей, имеющих значительную величину, применяют специальный прибор – планиметр (рис.21). Такой способ получил название механического.

Принцип измерения площади планиметром заключается в обводе контура обводным рычагом планиметра 3, на котором имеется счетный механизм 1, фиксирующий длину пройденного пути (u2-u1). Зная длину пройденного пути и цену деления планиметра, искомую площадь контура вычисляют по формуле

Р=c(u2-u1), (23)

Цену деления планиметра определяют перед началом работы путем обвода контура, площадь которого известна. При работе на топографических картах и планах для определения цены деления планиметра обводят квадрат километровой сетки. На карте масштаба 1:10 000 Р= 100 га. Таким образом, искомую цену деления в этом случае можно вычислить по формуле

с=100/(u2-u1), (24)

 

 

Рис.21. полярный планиметр а) общий вид; б) счетный механизм

 

 

Задача 7.2. Определить цену деления планиметра по упрощенной программе (при одном положении полюса).

Для определения цены деления выбирают на карте квадрат километровой сетки. Полюс планиметра 4 следует расположить так, чтобы при обводе угол между обводным 7 и полюсным рычагом 3 был более 30°, но менее 150°. Для контроля делают не менее 3-х обводов. Измерения считают качественными, если расхождения разностей (u2-u1) между приемами не превышают двух-трех делений в последнем разряде. В противном случае измерения повторяют. Результаты измерений записывают в таблицу 15.

Таблица 15

Определение цены деления планиметра №69556

№ изм.	Отсчеты по планиметру	Разности отсчетов	Цена деления планиметра
U1	U2	U2-U1
				0.09709
				0.09728
				0.09689

Сср=0.09709

 

Задача 7.3. Определить площадь контура, указанного преподавателем на карте.

Измерения выполняют аналогично определению цены деления планиметра, только обводят в этом случае заданный контур. Результаты измерений записывают в таблице 16.

 

Таблица 16

 

. Измерение площади треугольника АВС планиметром № 69556

№ изм.	Отсчеты по планиметру	Разности отсчетов	Площадь контура, га
U1	U2	U2-U1
				46.1
				46.0
				46.2

Pcp=46.1 га

Вопросы для самоконтроля

1.Какие существуют способы измерения площадей?

2. Какие формулы вычисления площадей из геометрии вы знаете?

3. Выведите формулу вычисления площади треугольника через прямоугольные координаты его вершин?

4. Расскажите устройство планиметра?

5. Как определить цену деления планиметра?

6. Как измерить площадь с помощью планиметра?

 

ЛИТЕРАТУРА

1. Курс инженерной геодезии: Учебник для вузов/ Под ред. В.Е. Новака. – М.: Недра,1989. – 430.

2. Б.Б.Данилевич, В.Ф.Лукьянов, Б.Ц.Хейфец и др. М.: Недра, 1987. – 334.

3. Условные знаки для топографических планов масштабов 1:5 000, 1:2 000, 1:1 000, 1:500./ГУГиК при СМ СССР. – М.: «Недра», 1989. - 286с.

 

 

№ варианта	Сближение γ	Склонение δ	№ варианта	Сближение γ	Склонение δ
	1°51	5°16		1°18	+4°18
	2°25	5°15		+2°18	+2°42
	1°15	-5°05		+2°42	-6°42
	-1 51	+5 16		-1 18	+4 42
	+2 25	+5 15		-0 18	+2 42
	+1 15	+5 05		+2 18	-6 42
	+1 51	-5 16		+1 18	-4 42
	-2 25	-5 15		+0 18	-2 42
	-1 15	-5 05		-2 18	-6 42
	+1 51	+5 05		-1 18	-4 42
	-2 25	+5 16		-0 18	-2 42
	-1 15	+5 05		+1 52	+6 17
	+2 1 8	+6 42		-1 49	+3 53

 

 

Введение

Методические указания “Решение инженерных задач на топографических картах и планах” предназначены для студентов строительных специальностей всех форм обучения при изучении дисциплины “Инженерная геодезия”.

Для выполнения задания студентам выдается ксерокопия топографической карты масштаба 1:25 000 или1:10 000 с нанесенными преподавателем исходными данными. Все построения и измерения производятся на карте, а решения выполняются на листах бумаги формата А4 и, при необходимости, дополняются графическими приложениями, которые вычерчивают в соответствии с условными знаками и шрифтами.

Студенты должны иметь: измеритель, линейку, карандаши Т, ТМ, 2М, транспортир, резинку, чертежную и миллиметровую бумагу, тушь различных цветов, чертежные перья и ручки, калькулятор.

Выполненная работа представляется на проверку преподавателю в сроки, предусмотренные календарным планом учебных занятий. При положительной оценке студентом производится защита работы.

 

1. Понятие карты и плана. Масштабы.

Для построения топографических планов поверхность Земли ортогонально проектируют на горизонтальную плоскость и уменьшают в определенное число раз. Поэтому топографическим планом называют уменьшенное и подобное изображение на бумаге отдельных небольших участков земной поверхности. Совокупность предметов местности называют ситуацией, а совокупность различных неровностей земной поверхности – рельефом. План местности, составленный без изображения рельефа, называют контурным. Например – лесоустроительный план. Таким образом, план – это чертеж, состоящий из горизонтальных проложений, полученных ортогональным проецированием соответствующих отрезков местности на горизонтальную плоскость.

Изображения больших по размерам участков земной поверхности на плоскости нельзя получить без искажений, т.е., с сохранением полного подобия. Такие участки сначала ортогонально проектируют на поверхность эллипсоида, а затем с поверхности эллипсоида по определенным математическим законам, называемым картографическими проекциями, переносят на плоскость. Таким образом, картой называют уменьшенное и закономерно искаженное изображение всей земли или отдельных частей ее поверхности на плоскости.

Степень уменьшения горизонтальных отрезков местности при перенесении их на бумагу называется масштабом плана (карты).

Масштабы бывают численные и графические. Численным масштабом называют отношение длины отрезка на карте или плане к длине соответствующей горизонтальной проекции линии на местности. Численный масштаб записывают в виде аликвотной дроби, т.е. дроби, числитель которой равен единице. Например, 1:5 000, 1:2 000, 1:25 000 и т.д. Знаменатель этой дроби показывает во сколько раз уменьшены предметы при изображении их на топографических планах, картах и профилях. На всех этих материалах подписывают численный масштаб.

Зная численный масштаб можно от единиц измерения на карте или плане переходить к единицам измерения на местности и наоборот. Например, если на карте масштаба 1:5 000 длина отрезка равна 2 см, то на местности длина его горизонтального проложения составит D=d*N=2*5000=10000 см=100м. Существенное влияние на точность измерения отрезков по любому чертежу оказывают возможности зрительного восприятия графических элементов. Невооруженный глаз человека не способен на чертеже на расстоянии 20-25 см отличить точку от отрезка, если его длина меньше 0,1 мм.

Поэтому точностью масштаба называют длину горизонтальной проекции линии местности соответствующую 0.1 мм на карте или плане. Для масштабов 1:500, 1:1 000, 1:10 000, 1:25 000 точность масштаба соответственно равна 0,05; 0,1; 1,0; 2,5 м.

Наряду с численным масштабом на практике широкое распространение получили графические масштабы,- линейный и поперечный. Пользование линейным масштабом понятно из рис.1

 

 

 

Поперечный масштаб (рис.2) применяется для более точных измерений длин линий на картах. Его гравируют на специальных металлических линейках. Точность измерения расстояния с помощью такого масштаба равна 0,5 цены наименьшего деления. С целью приобретения навыков пользования поперечным масштабом необходимо решить задачи 1 – 4.

Задача 1.1. Построить нормальный сотенный поперечный масштаб

Для его построения на прямой линии откладывают ряд равных отрезков, которые называют основанием масштаба (2 см). Из концов оснований восстанавливают перпендикуляры произвольной длины. На крайних перпендикулярах измерителем откладывают по десять отрезков одинаковой длины и соединяют их концы. Крайнее левое основание сверху и снизу делят на десят одинаковых частей методом деления отрезка на пропорциональные части. Соединяют нулевую точку (О) нижнего основания с первым делением верхнего основания (А) и т.д. Таким образом получают масштабную линейку (рис.2).

 

 

Для пользования поперечным масштабом необходимо мысленно оцифровать его деления, исходя из масштаба плана или карты. Так, если масштаб плана 1:500, то основание равно 10 м., АВ= 1м и наименьшее деление (а1 в1) равно 0.1 м. Измеритель располагают таким образом, чтобы правая игла находилась на одной из вертикальных линий, а левая – на трансверсале (рис.3). при этом обе иглы должны находиться на одной горизонтальной линии.

 

 

После чего считают, сколько целых (k), десятых ( n ) и сотых ( m) долей основания содержится между иглами и, исходя из ранее выполненной оцифровки, вычисляют расстояние

 

d=k(OK)+n(0.1 OK)+m(0.01 OK) (1)

 

Для случая, приведенного на рис.3 имеем к=1, п=4, т=3.5, а следовательно d=1 *10+4 * 1+3.5 * 0.1 = 14.35(м).

Задача 1.2. Измерить длины сторон трех произвольных по форме треугольников с помощью поперечного масштаба, считая, что первый из них построен в масштабе 1:5 000, второй – 1:10 000 и третий – 1:25 000.

Для решения задачи построить три произвольных треугольника, для чего наколоть иглой измерителя вершины, обвести их кружками диаметром 1 мм и соединить прямыми линиями (рис.4). Измерения выполнить с помощью измерителя и построенного в задаче 1.1 поперечного масштаба. Значения длин линий, с учетом точности масштаба, записать в метрах у соответствующих им сторон треугольников. Например, при измерении отрезка на плане масштаба 1:500 его длина оказалась равной 15 м. Запись 15 м будет считаться не правильной, так как она не отражает точности масштаба плана. Учитывая, что точность масштаба 1:500 равна 0.05 м, результат следует записать в виде 15.00 м. Высота цифр равна 2 мм (шрифт вычислительный).

 

 

 

Задача 1.3. По длинам сторон, заданным преподавателем, построить три треугольника в масштабах 1:500, 1:1 000, 1:2 000. Оформить как показано на рис.5.

Для решения задачи на прямой отложить с помощью измерителя основание треугольника АВ в соответствующем масштабе. Из концов отрезка засечкой получить положение точки С. Вершины А,В,С треугольника обвести кружками диаметром 1 мм, соединить прямыми и подписать длины сторон в соответствии с точностью масштаба.

 

 

Задача 1.4. Определить масштаб аэроснимка

Задача выполняется в аудиторное время. Для ее решения студентам выдается аэроснимок и топографическая карта. Необходимо на аэроснимке выбрать четыре хорошо опознаваемых контура и условно обозначить их буквами а, b, c, d. Измерить расстояние между ними с точностью до 0.1 мм. Результаты записать в табл. 1.