
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сбор нагрузок на поперечную рамуСодержание книги
Поиск на нашем сайте Постоянная нагрузка Постоянная нагрузка на ригель рамы
Рисунок 68. Нагрузка на стойку от покрытия
Распределенная нагрузка на конструкцию покрытия Постоянная нагрузка передается на стойку в виде сосредоточенной силы, которая определяется из выражения:
Нагрузка на стойку может передаваться без эксцентриситета, т.е. Постоянная нагрузка от собственного веса стеновых панелей Для упрощения расчета конструктивное решение стеновых панелей принимаем таким же, что и панелей покрытия, т.е. величина Для статического расчета рамы допускается нагрузки от стеновых панелей сосредоточить в одной точке на расстоянии от обреза фундамента, равном Отсюда следует, что нагрузка от стеновых панелей (
где
Рисунок 69. Нагрузка на стойку от стеновых панелей
H – высота стенового ограждения B =6, 3м - шаг поперечных рам; H =7, 3 м - высота стойки; Нагрузка от стеновых панелей на стойку передается с эксцентриситетом:
где h – высота сечения стойки;
Сила Постоянная нагрузка от собственного веса стойки
Для определения нагрузки от собственного веса стойки предварительно задаемся размерами сечения: - высота сечения стойки - ширина сечения стойки Коэффициент надежности по нагрузке
Собственный вес стойки (
Нагрузка от собственного веса стойки прикладывается в виде сосредоточенной силы на уровне обреза фундамента. Временная нагрузка Снеговая нагрузка Снеговая нагрузка для статического расчета принимается как равномерно распределенная по ригелю. Величина распределенной нагрузки будет равна:
где S – расчетная нагрузка, зависящая от района строительства (VII),
B =6,3м - шаг поперечных рам. Снеговая нагрузка на стойку передается в виде сосредоточенной силы равной:
где Считаем, что нагрузка передается без эксцентриситета, в соответствии с этим
Ветровая нагрузка
Нормативное значение средней составляющей ветровой нагрузки wm на высоте z над поверхностью земли следует определять по формуле:
где w0 - нормативное значение ветрового давления [4 п. 6.4, табл.5], w0= 0,3 кПа для II ветрового района; kz - коэффициент, учитывающий изменение ветрового давления по высоте [4 п. 6.5, табл.6]; с - аэродинамический коэффициент [4 п. 6.6, прил.4]. Принимаю с наветренной стороны для напора В общем виде расчетная ветровая нагрузка, действующая на стойку на высоте z от уровня земли будет равна:
где B=6,3м - шаг поперечных рам;
Значение z 2= Hст =7, 3 м, где
По данным значениям строится действительный характер распределения ветровой нагрузки по высоте для напора и тоже самое для отсоса.
С целью упрощения, для статического расчета нагрузка от обреза фундамента до низа ригеля приводится к равномерно распределенной по стойке.
Величина равномерно распределенной нагрузки Соответственно
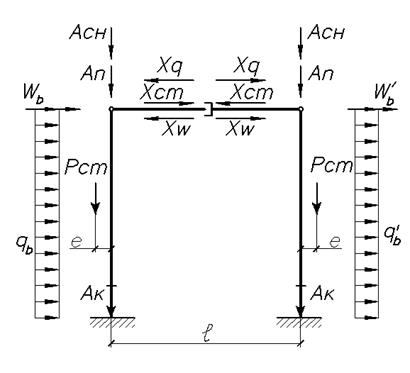
Ветровая нагрузка от низа ригеля до конька приводится к сосредоточенной силе, приложенной по низу ригеля. Сосредоточенная сила определяется как площадь трапеции и для напора будет равна: Для напора: Для отсоса: Расчетная схема рамы приведена на рисунке 83. где Pпокр – нагрузка от собственного веса покрытия, Рсн – нагрузка от стенового ограждения, Рк – от собственного веса колонны,
Двухшарнирная рама является один раз статически неопределимой системой. За неизвестное удобно принимать продольное усилие в ригеле, который считается абсолютно жестким. Величина X находится как сумма Xi, определенных из канонических уравнений метода сил для каждого вида загружения отдельно:
Рисунок 71. Расчетная схема рамы
Виды загружений, вызывающих усилия в ригеле: а) ветровая линейная нагрузка
б) ветровая сосредоточенная нагрузка
в) нагрузка от стеновых панелей, приложенных с эксцентриситетом
Анализируя результаты статического расчета рамы, можно сделать вывод о том, что опасным сечением, в котором возникают максимальные сила N, изгибающий момент M и поперечная сила Q является сечение 1-1 на уровне обреза фундамента (в заделке). Для определения усилий в опасном сечении, из двухшарнирной рамы вырезаем стойку, к ней прикладываем местную нагрузку, действие отброшенных связей заменяем соответствующими реакциями. Определение внутренних силовых факторов M, N, Q ведем как для консольной балки. Расчетные усилия от кратковременных нагрузок принимаем с коэффициентом сочетания
Рисунок 72. Расчетная схема двухшарнирной рамы для определения усилий в стойке
Усилия определяем для левой и правой стоек. Максимальные усилия возникают в нижнем сечении колонн у заделки в фундамент. Изгибающие моменты в левой и правой стойке определяются из выражения:
Поперечные силы в стойках:
Продольное усилие сжатия:
Расчет клееной стойки
Площадь сечения Моменты сопротивления:
Моменты инерции:
Гибкость стойки относительно оси X определяется из выражения:
где
Гибкость должна быть не более При большей гибкости необходимо изменить размеры поперечного сечения стойки. Гибкость стойки относительно оси Y будет равна:
где Поскольку гибкость превышает предельно допустимую, необходимо ввести распорки. Тогда расчетная длина из плоскости будет равна расстоянию между узлами вертикальных связей, поставленных по колоннам в плоскости продольных стен
Определив геометрические характеристики сечения и усилия в колонне, выполняем проверки по прочности и устойчивости. Проверка по устойчивости по оси Х выполняется по формуле:
где N, M – расчетные значения продольной силы и изгибающего момента в заделке; Fнт – площадь сечения нетто;
где
Рисунок 74. Вертикальные связи по стойкам
Проверяю устойчивость:
Относительно оси Y прочность стойки проверяем как центрально-сжатого элемента по формуле:
где
где коэффициент а =0,8 для древесины.
Выполняем проверку Проверка устойчивости плоской формы деформирования производится по формуле:
где F бр – площадь брутто с максимальными размерами сечения элемента на участке l у; W бр – максимальный момент сопротивления брутто на рассматриваемом участке l у относительно оси У; n = 2 – для элементов без закрепления растянутой зоны из плоскости деформирования; j =
jм – коэффициент, определяемый по формуле где b – ширина поперечного сечения; h – максимальная высота поперечного сечения на участке ly; kф= 2,45 – коэффициент, зависящий от формы эпюры изгибающих моментов на участке lу, определяемый по табл. 2 прил. 4 [1].
Выполняем проверку:
Проверка клеевого шва на скалывание:
где
Qвн – определяется по формуле
|
||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 1349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |


 39, 6 кН/м.
39, 6 кН/м.
 . Тогда изгибающий момент и поперечная сила от постоянной нагрузки на ригель рамы будут равны 0 и стойка будут испытывать только сжатие, сжимающая сила равна
. Тогда изгибающий момент и поперечная сила от постоянной нагрузки на ригель рамы будут равны 0 и стойка будут испытывать только сжатие, сжимающая сила равна 
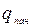 известна.
известна. .
. ) равна:
) равна:
 ,
,
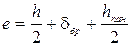
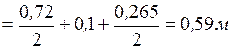 .
. ;
; =0, 265м - высота панели;
=0, 265м - высота панели; , приложенная с эксцентриситетом “е”, приводит к появлению в стойке изгибающего момента, равного:
, приложенная с эксцентриситетом “е”, приводит к появлению в стойке изгибающего момента, равного:  .
. 0, 73 м;
0, 73 м; 0, 15 м.
0, 15 м. .
. кг/м3 - плотность клееной лиственницы [1, прил. 3].
кг/м3 - плотность клееной лиственницы [1, прил. 3]. ):
): =0, 15 . 0, 73 . 7, 3 . 1, 1 . 650 = 571,54 кг.
=0, 15 . 0, 73 . 7, 3 . 1, 1 . 650 = 571,54 кг. =
=  кг/м,
кг/м, [4, п. 5.2, табл.4];
[4, п. 5.2, табл.4]; - коэффициент, зависящий от формы покрытия, принимается согласно [4, прил. 3*],
- коэффициент, зависящий от формы покрытия, принимается согласно [4, прил. 3*],  =136, 08 кН,
=136, 08 кН, - пролет поперечной рамы.
- пролет поперечной рамы.

 =136, 08 кН/м.
=136, 08 кН/м.
 , для отсоса
, для отсоса  .
. [кН/м],
[кН/м], =1,4 – коэффициент надежности по нагрузке.
=1,4 – коэффициент надежности по нагрузке. определяется для характерных точек стойки, а именно на расстоянии от обреза фундамента равного z 1= 5 м,
определяется для характерных точек стойки, а именно на расстоянии от обреза фундамента равного z 1= 5 м, =7, 3+0, 924+0, 263=8, 48 м, z 4= 10 м.
=7, 3+0, 924+0, 263=8, 48 м, z 4= 10 м. - высота стойки;
- высота стойки; - высота ригеля в центре пролета;
- высота ригеля в центре пролета; - высота панели покрытия.
- высота панели покрытия.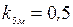 ;
;  ;
; 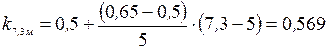 ; для городских территорий, лесных массивов и других местностей, равномерно покрытых препятствиями высотой более 10 м; (тип местности В [1 п. 6.5])
; для городских территорий, лесных массивов и других местностей, равномерно покрытых препятствиями высотой более 10 м; (тип местности В [1 п. 6.5]) .
. ;
; ;
;

 ;
; ;
; ;
; ;
; Рисунок 70. Ветровая нагрузка на раму
Рисунок 70. Ветровая нагрузка на раму находится из равенства площадей эпюр действительной распределенной ветровой нагрузки и эквивалентной равномерно распределенной
находится из равенства площадей эпюр действительной распределенной ветровой нагрузки и эквивалентной равномерно распределенной 
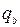 определяем из выражения:
определяем из выражения: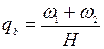 [кН/м].
[кН/м].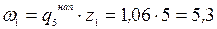 кН;
кН; кН;
кН; кН;
кН; кН;
кН; кН/м;
кН/м;  кН/м.
кН/м. [кН],
[кН], кН;
кН; кН.
кН. - линейные и сосредоточенные нагрузки от действия ветра на раму.
- линейные и сосредоточенные нагрузки от действия ветра на раму.
 ;
;  ;
; ;
; ;
; ;
; .
. .
.





 ,
, 

 Определив усилия M, N, Q в опасном сечении стойки, переходим к подбору сечения стойки. Предварительно, на основании опыта проектирования подобных элементов, задаемся сечением стойки. Высота стойки определена ориентировочно
Определив усилия M, N, Q в опасном сечении стойки, переходим к подбору сечения стойки. Предварительно, на основании опыта проектирования подобных элементов, задаемся сечением стойки. Высота стойки определена ориентировочно  =0, 73 м, ширина стойки
=0, 73 м, ширина стойки  =0, 15 м. Сечение стойки развито в плоскости рамы. Набирается сечение стойки из досок плашмя. Толщина доски не более 40 мм, после двухсторонней острожки толщина доски
=0, 15 м. Сечение стойки развито в плоскости рамы. Набирается сечение стойки из досок плашмя. Толщина доски не более 40 мм, после двухсторонней острожки толщина доски  . Высота сечения стойки уточняется соответственно с толщиной доски h=0,726м. Влажность клееной древесины должна быть не более
. Высота сечения стойки уточняется соответственно с толщиной доски h=0,726м. Влажность клееной древесины должна быть не более  . Для принятого сечения стойки определяется геометрические характеристики сечения и гибкость
. Для принятого сечения стойки определяется геометрические характеристики сечения и гибкость  и
и  .
. .
. ;
; ;
; ;
;  ;
; ,
, - расчетная длина стойки,
- расчетная длина стойки,  , при жестком защемлении в фундаменте
, при жестком защемлении в фундаменте - радиус инерции для прямоугольного сечения, равен
- радиус инерции для прямоугольного сечения, равен  .
.
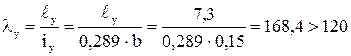 ,
, - расчетная длина стойки относительно оси Y, которая зависит от наличия связей и распора по стойкам. Относительно оси Y гибкость также не должна превышать предельного значения
- расчетная длина стойки относительно оси Y, которая зависит от наличия связей и распора по стойкам. Относительно оси Y гибкость также не должна превышать предельного значения  . Предварительно принимаем
. Предварительно принимаем  – это расстояние между узлами закрепления стойки.
– это расстояние между узлами закрепления стойки. .
.
 ;
; - момент сопротивления нетто относительно оси X;
- момент сопротивления нетто относительно оси X; – коэффициент, учитывающий влияние продольного изгиба
– коэффициент, учитывающий влияние продольного изгиба ,
,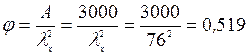 при
при  .
.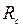 - расчетное сопротивление древесины при работе на сжатие;
- расчетное сопротивление древесины при работе на сжатие; [1 п. 3.1, табл.3];
[1 п. 3.1, табл.3]; ;
;
 .
.
 – коэффициент продольного изгиба определяется в зависимости от гибкости
– коэффициент продольного изгиба определяется в зависимости от гибкости  . Поскольку
. Поскольку  , то значение
, то значение  ,
, .
. .
.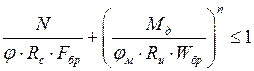 ,
, – коэффициент продольного изгиба, определяемый для гибкости участка элемента расчетной длиной lу из плоскости деформирования;
– коэффициент продольного изгиба, определяемый для гибкости участка элемента расчетной длиной lу из плоскости деформирования; ;
; ,
, .
. - расчетные сопротивления древесины при работе на сжатие и изгиб соответственно;
- расчетные сопротивления древесины при работе на сжатие и изгиб соответственно;  [1 п. 3.1, табл.3].
[1 п. 3.1, табл.3]. .
.
 ,
,  ;
; ;
;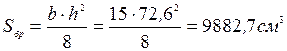 ;
; ;
; - расчетное сопротивление древесины при работе на скалывание клееной древесины вдоль волокон;
- расчетное сопротивление древесины при работе на скалывание клееной древесины вдоль волокон;  [1 п. 3.1, табл.3].
[1 п. 3.1, табл.3]. .
.


