
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристика оптического диапазона электромагнитных волн. Особенности видимого диапазона.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Характеристика оптического диапазона электромагнитных волн. Особенности видимого диапазона. Большое значение оптической области спектра электромагнитных волн для практической деятельности человека обусловлено, прежде всего, тем, что внутри нее в узком интервале длин волн от 0,4 до 0,7 мкм лежит участок видимого света, непосредственно воспринимаемого человеческим глазом. Данный диапазон определяется как спектральными характеристиками солнечного излучения, достигающего поверхности Земли, так и особенностями эволюционного развития человека. Коротковолновое (менее 0,3 мкм) излучение Солнца практически полностью поглощается озоном в верхних слоях земной атмосферы. Наиболее подходящим для зрения является диапазон вблизи максимума солнечного излучения (~ 0,5 мкм). Микроволновый же диапазон непригоден для “качественного” зрения из-за присутствия здесь больших тепловых “шумов”. В понятие оптического диапазона включают обычно еще инфракрасное и ультрафиолетовое излучение. Но и для них принятые границы спектра в значительной степени условны. По существу, они определяются используемыми способами получения и регистрации электромагнитных волн. Определим место видимого диапазона на шкале электромагнитных волн. Как известно из курса электричества, частота электромагнитной волны (ЭМВ) связана с ее длиной в вакууме соотношением: n= с / l, где с – скорость распространения ЭМВ в вакууме. Энергия квантов света, как показано в квантовой теории, равна: Е к = h n = ħw, где w = 2pn – круговая частота, h = 2pħ – постоянная Планка. Пользуясь указанными величинами, составим таблицу ЭМВ:
Плоская электромагнитная волна, ее структура и представление в комплексной форме. Для анализа структуры плоской ЭМВ воспользуемся записью уравнений Максвелла с помощью определения и свойств оператора Гамильтона (набла-оператора):
Тогда уравнения Максвелла примут вид: Решение этих уравнений ищем в виде:
где E 0 и B 0 – постоянные векторы, не зависящие от координат и времени (в общем случае компоненты этих векторов могут быть комплексными). Учитывая, что (2.43) Максвелла Из этих соотношений можно сделать следующие выводы: 1. Плоская ЭМВ является поперечной. E, B и k составляют тройку взаимно перпендикулярных векторов. Поперечность световых колебаний была открыта в 1817 г. Юнгом 2. E =cB. 3. Т.к. k, w, m0, e0 – вещественные величины, то это значит, что E и B в плоской ЭМВ колеблются в одинаковой фазе.
Сферические волны. Сходящиеся и расходящиеся сферические волны.
Рассмотрим изотропную волну от точечного источника. Тогда решение уравнения (2.10) будем искать в виде Ф(r,t), где r – расстояние от точечного источника. В сферической системе координат (r, q, j):
Суперпозиция ЭМВ. Напряженность электрического поля и магнитная индукция равны соответственно сумме напряженностей и магнитных индукций всех полей в данной точке независимо от их происхождения, частоты и направления распространения. Однако полученная в результате сложения полей совокупность электромагнитных полей, вообще говоря, не составляет бегущую электромагнитную волну. Суперпозиция бегущих плоских монохроматичных ЭМВ. Пусть заданы две волны, для которых k1 = k2 = k, w1 = w2 = w и
Полное внутреннее отражение света. Примеры его проявления и использования. Явление полного внутреннего отражения. При падении света на границу двух диэлектриков, для которых
Когда угол падения
Но формулы Френеля останутся справедливыми и в этом случае, если закон преломления рассматривать просто как определение входящих в них величин sinq2 и cosq2. Справедливость понимаемых таким образом формул Френеля следует из того, что они обеспечивают выполнение граничных условий и в этом случае. Формулы Френеля для отраженной волны ((4.56) и (4.67) с учетом (4.86)) имеют вид:
Видно, что энергетические коэффициенты
движутся вдоль поверхности раздела и затем возвращаются в первую среду. Места входа энергии во вторую среду и ее возвращения в первую смещены друг относительно друга. Амплитуды p– и s– компонент отраженной волны не изменяются по абсолютному значению, но испытывают различные фазовые сдвиги. Если представить, что
Примеры: 1. Призма–крыша, световоды, миражи, ромб (параллелепипед) Френеля (φ=54,37)
15. Распространение света в проводящих средах. Комплексный показатель преломления. Отражение света от поверхности проводника. Глубина проникновения. Закон Бугера. Распространение света в проводящих средах. При рассмотрении вопроса применения электромагнитной теории Максвелла к данному случаю, задача сводится к учету проводимости металла, т.е. формально к введению в уравнения Максвелла членов, зависящих от коэффициента электропроводности s. Отражение света от поверхности металла, как и его распространение в нем, может быть рассмотрено на основе материальных уравнений, в которых диэлектрическая проницаемость e(w) комплексна. Соответственно показатель преломления n – тоже комплексный: В сильно поглощающих средах и металлах мнимая часть преобладает над вещественной. Частичное проникновение света в металл создает токи проводимости. С ними связано выделение джоулевой теплоты, т.е. поглощение света – необратимое превращение электромагнитной энергии в энергию хаотического теплового движения. Чем выше проводимость металла, тем меньшая доля падающего света проникает в металл и поглощается там. В идеальном проводнике, которому формально соответствует Пусть из вакуума на металл падает плоская монохроматическая волна с волновым вектором
Видно, что составляющая вектора k 2, направленная вдоль границы вещественна. Поэтому мнимая часть вектора k 2 перпендикулярна поверхности металла. Это значит, что плоскости равных амплитуд прошедшей волны параллельны границе раздела. Вектор Формулы Френеля остаются в силе, если в них рассматривать cosq2 как комплексную величину: Знак корня нужно взять так, чтобы неоднородная волна затухала вглубь металла. Тогда коэффициенты отражения тоже комплексны: При нормальном падении:
При достаточно высоких частотах роль “силы трения” в уравнениях колебаний электрона становится несущественной. Случай g = 0 формально соответствует “идеальному” металлу сs®¥. При В этом случае из (4.102) следует  = 1, т.е. отражение от поверхности идеального проводника полное. Закон Бугера. Для затухающей волны, распространяющейся вдоль оси Z, интенсивность излучения: Отсюда получаем зависимость:
Толстая линза
Рис. 4.21. Ход лучей в толстой линзе. Концепция тонкой линзы представляет собой упрощение более сложной и всеобъемлющей концепции толстой линзы. Рассмотрим сферическую линзу значительной толщины. Характеристики изображения, создаваемого такой линзой, могут быть описаны посредством введения двух фокусов, двух главных плоскостей, оптической оси и двух узловых точек. Две главные плоскости Р толстой линзы перпендикулярны ее оптической оси и пересекают эту ось в узловых точках N. Луч преломляется на первой поверхности линзы, проходит через оптический центр на оптической оси и преломляетсяеще раз на второй поверхности. Точка на оси системы, в которой сходятся лучи, падающие на оптическую систему параллельно оптической оси (т.е. точка с увеличением M = 0) и точка, выйдя из которой лучи после прохождения оптической системы становятся параллельными оптической оси (т.е. с увеличением M = ¥), называются фокусами оптической системы. Ход лучей в тонкой линзе Рассмотрим построение хода луча произвольного направления в тонкой собирающей линзе. Для этого воспользуемся двумя свойствами тонкой линзы:1) луч, прошедший через оптический центр линзы, не меняет своего направления; 2) Параллельные лучи, проходящие через линзу, сходятся в фокальной плоскости. Тонкие линзы. Пусть
Тонкой линзой называется линза, для которых можно пренебречь третьим слагаемым в скобках (5.55), что соответствует малости толщины линзы по сравнению с каждым радиусом кривизны:
Тонкая линза представляется не имеющей толщины и с ней совпадают обе главные плоскости. Фокусное расстояние становится равным отсчёту от линзы до фокуса. При этом условии матрица с коэффициентами Гаусса для тонкой линзы принимает вид:
Величина Двулучевая интерференция, осуществляемая делением волнового фронта. Схема Юнга. Примеры практических схем двулучевой интерференции. Многие оптические двух лучевые интерференционные схемы могут быть сведены к идеализированной схеме. Конечно, в реальных схемах используются не два, а один источник света, но лучи от этого источника попадают на экран, где наблюдается интерференция, по двум различным путям. Расщепление первоначальной волны от источника на две и последующее их сведение на экране — общий признак всех двухлучевых интерференционных схем. Опыт Юнга (1801 г.). Рассмотрим интерференцию, возникающую в результате выделения с помощью двух щелей S 1и S 2 участков сферического волнового фронта волны от точечного источника S (рис.6.3) (метод деления волнового фронта).
Найдем разность хода лучей в произвольной точке наблюдения P на экране:
При
(6.13) Следовательно, с точностью до величины первого порядка по
Примеры экспериментальных интерференционных схем, осуществляющих метод деления волнового фронта: бипризма Френеля, билинза Бийе, бизеркало Френеля, зеркало Ллойда.
Многолучевая интерференция. Исследуем сначала интерференцию многих световых волн при прохождении плоской монохроматической волны через плоскопараллельную диэлектрическую пластинку толщиной h и показателем преломления n. Обозначим
где Á и Â – энергетические коэффициенты пропускания и отражения соответственно. Будем считать углы падения j и преломления q достаточно малыми, что можно считать коэффициенты отражения и пропускания независящими от этих углов. Разность хода D между соседними интерферирующими волнами на выходе пластины равна
а разность фаз равна Запаздывание последующей волны относительно предыдущей за счет прохождения волны в пластинке учтем множителем е- id. Суммарная амплитуда E 2 прошедшей волны определяется суперпозицией всех прошедших пластинку волн:
Интенсивность света определяется следующим образом: т.е. при ® 1 Þ V ® 1.
Сканирующий интерферометр Фабри–Перо. Формула Эйри объясняет принцип действия широко используемого в оптике и лазерной технике спектрального прибора – сканирующего интерферометра Фабри–Перо. Это своеобразный аналог измерителей частотных характеристик электрических сигналов радиодиапазона, основанных на принципе сканирования резонансной частоты колебательной системы – колебательного контура, коаксиального, полоскового или объемного резонатора. Заметим, что разность фаз линейно зависит от расстояния между пластинами. Если зафиксировать угол j, то это соответствует помещению некоторого фотоприемника в любую точку экрана (рис.6.8)
Дифракция на щели. Рассмотрим падение плоской монохроматической световой волны на бесконечную щель шириной b (рис.7.9).
После несложного интегрирования и перехода от поля к интенсивности, получаем интенсивность дифракционной картины: Проанализируем выражение (7.41). 1. При j = 0 u =0. Используя соотношение 2. При углах j, для которых sin u = 0, а u ¹ 0 интенсивность света обращается в нуль. Тогда условие минимума дифракционной картины на одиночной щели принимает вид: 3. Основная часть потока энергии сосредоточена в пределах изменения угла дифракции j между первыми (n = ±1) симметричными максимумами. График зависимости (7.41) приведен на рис.7.10.
4. Чем меньше (уже) щель, тем шире центральный максимум. Нетрудно заметить, что при b»l центральный максимум расплывается на всю полуплоскость (j»p/2). Дальнейшее уменьшение щели приводит лишь к монотонному уменьшению интенсивности прошедшего света. Изучение картины дифракции дает информацию о ширине щели, если известна длина волны используемого света. Наоборот, зная ширину щели, можно найти длину волны. Таким образом, дифракционная картина от данного объекта имеет характерный вид, позволяющий получать информацию о размерах этого объекта. Отмеченное обстоятельство носит достаточно общий характер и лежит в основе метрологического применения дифракционных явлений.
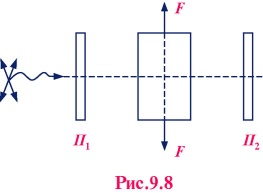
Анизотропия при деформациях Обычные прозрачные тела, не обладающие двойным лучепреломлением, при деформации сжатия или растяжения приобретают свойства одноосного кристалла, оптическая ось которого направлена вдоль деформирующих сил. Экспериментально установили следующую связь между показателями преломления необыкновенной и обыкновенной волн в направлении ортогональном так называемой оптической оси, т.е. направления внешних сил деформации:ne – no = kσ, (9.19) где σ – напряжение (Па = Н/м2), коэффициент, зависящий от свойств вещества. Разность (ne – no) может принимать как положительные, так и отрицательные значения. Вообще говоря, возможна дисперсия показателей ne и no, т.е. зависимость их от длины волны λ.
При изменении напряжения картина меняется. Таким образом, наблюдая распределение цветовой освещенности по объему тела, можно судить о распределении напряжений на разных участках. Это свойство используют при исследовании распределения напряжений в сложных трудно рассчитываемых конструкциях – изготавливают геометрически подобную модель из прозрачного материала. Подвергают различным нагрузкам и по наблюдаемой в рассмотренной на Рис. 9.8 установке картине судят о распределении внутренних напряжений. 2. Анизотропия, создаваемая в веществе электрическим полем. Оптически изотропное вещество в электрическом поле приобретает оптические свойства одноосного кристалла с оптической осью параллельной электрическому вектору Схема установки Керра показана на Рис. 9.9. При распространении света перпендикулярно направлению вектора ne – no= K λE2, (9.20) где K – постоянная Керра, принимающая разные значения для разных веществ. Отметим, что K> 0 для боль-шинства веществ, т.е. ne>no, что соответствует положительному кристаллу. Правда, встречаются и вещества (гораздо реже), у которых K< 0, например: этиловый эфир, спирт. Для жидкостей постоянная Керра имеет порядок (1÷10) пм/В2 (1 пм = 10-12). Для газов постоянная по естественным причинам значительно меньше, например, у кислорода при нормальных условиях K = 0,45 ∙10-15 м/В2. Характеристика оптического диапазона электромагнитных волн. Особенности видимого диапазона. Большое значение оптической области спектра электромагнитных волн для практической деятельности человека обусловлено, прежде всего, тем, что внутри нее в узком интервале длин волн от 0,4 до 0,7 мкм лежит участок видимого света, непосредственно воспринимаемого человеческим глазом. Данный диапазон определяется как спектральными характеристиками солнечного излучения, достигающего поверхности Земли, так и особенностями эволюционного развития человека. Коротковолновое (менее 0,3 мкм) излучение Солнца практически полностью поглощается озоном в верхних слоях земной атмосферы. Наиболее подходящим для зрения является диапазон вблизи максимума солнечного излучения (~ 0,5 мкм). Микроволновый же диапазон непригоден для “качественного” зрения из-за присутствия здесь больших тепловых “шумов”. В понятие оптического диапазона включают обычно еще инфракрасное и ультрафиолетовое излучение. Но и для них принятые границы спектра в значительной степени условны. По существу, они определяются используемыми способами получения и регистрации электромагнитных волн. Определим место видимого диапазона на шкале электромагнитных волн. Как известно из курса электричества, частота электромагнитной волны (ЭМВ) связана с ее длиной в вакууме соотношением: n= с / l, где с – скорость распространения ЭМВ в вакууме. Энергия квантов света, как показано в квантовой теории, равна: Е к = h n = ħw, где w = 2pn – круговая частота, h = 2pħ – постоянная Планка. Пользуясь указанными величинами, составим таблицу ЭМВ:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 790; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.44.115 (0.01 с.) |

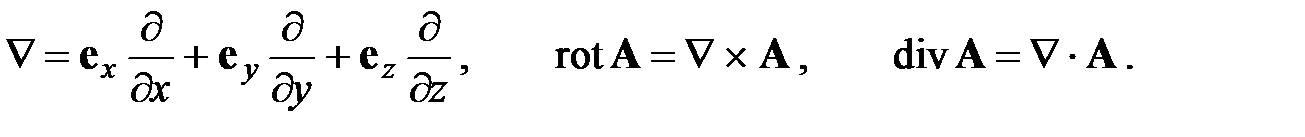

 (2.41)
(2.41) (2.42)
(2.42)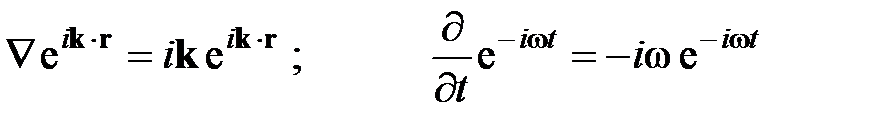 и подставляя решения (2.41) и (2.42) в уравнения
и подставляя решения (2.41) и (2.42) в уравнения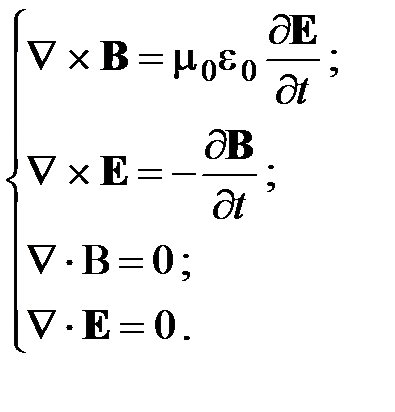 , получаем следующие важные соотношения, описывающие структуру плоской ЭМВ:
, получаем следующие важные соотношения, описывающие структуру плоской ЭМВ: 
 (2.10)
(2.10) (2.21) а искомое решение из соображений симметрии не зависит от угловых координат. Тогда волновое уравнение примет вид:
(2.21) а искомое решение из соображений симметрии не зависит от угловых координат. Тогда волновое уравнение примет вид: (2.22) т.е. имеет вид (2.11), если произвести замену z® r, Ф®rФ. Тогда общее решение уравнения (2.22) имеет вид:
(2.22) т.е. имеет вид (2.11), если произвести замену z® r, Ф®rФ. Тогда общее решение уравнения (2.22) имеет вид:  (2.23) Выясним физический смысл полученного решения. Второе слагаемое представляет собой волну, движущуюся в направлении увеличения значений r, т.е. от центра (точечного источника). Такая волна называется расходящейся. Первое слагаемое описывает волну, движущуюся в направлении уменьшения r, т.е. к центру. Такая волна называется сходящейся. Общее решение является суперпозицией сходящейся и расходящейся волн. Значение Ф в фиксированный момент времени на сфере постоянного радиуса является постоянным. Такие волны называются сферическими.
(2.23) Выясним физический смысл полученного решения. Второе слагаемое представляет собой волну, движущуюся в направлении увеличения значений r, т.е. от центра (точечного источника). Такая волна называется расходящейся. Первое слагаемое описывает волну, движущуюся в направлении уменьшения r, т.е. к центру. Такая волна называется сходящейся. Общее решение является суперпозицией сходящейся и расходящейся волн. Значение Ф в фиксированный момент времени на сфере постоянного радиуса является постоянным. Такие волны называются сферическими.
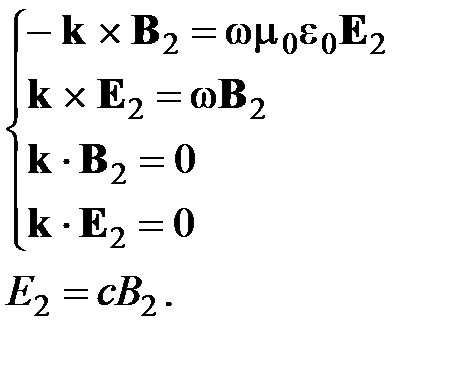 2.55 2.56
2.55 2.56 , из закона Снеллиуса следует, что существует предельный (или критический) угол qп падения, при котором угол преломления
, из закона Снеллиуса следует, что существует предельный (или критический) угол qп падения, при котором угол преломления  . Тогда
. Тогда  .При
.При  угол преломления q2 имеет обычную геометрическую интерпретацию, и коэффициенты R и T являются вещественными.
угол преломления q2 имеет обычную геометрическую интерпретацию, и коэффициенты R и T являются вещественными.
 , не существует вещественного угла преломления q2, т.к. закон Снеллиуса дает для sinq2 значение больше единицы, а для cosq2 – чисто мнимое значение:
, не существует вещественного угла преломления q2, т.к. закон Снеллиуса дает для sinq2 значение больше единицы, а для cosq2 – чисто мнимое значение:
 ;
;  .
. при углах падения больше критического. Поэтому это явление называется полным внутренним отражением (ПВО). При этом волна и соответствующая доля энергии проникают через границу раздела во вторую среду на некоторую глубину d (глубину проникновения) (амплитуда поля на глубине d падает в е раз)
при углах падения больше критического. Поэтому это явление называется полным внутренним отражением (ПВО). При этом волна и соответствующая доля энергии проникают через границу раздела во вторую среду на некоторую глубину d (глубину проникновения) (амплитуда поля на глубине d падает в е раз) ,
, , то
, то 
 Обозначим
Обозначим  Тогда
Тогда  .
.
 .(4.96)
.(4.96) , потери на джоулеву теплоту вообще отсутствуют, так что падающий свет полностью отражается.
, потери на джоулеву теплоту вообще отсутствуют, так что падающий свет полностью отражается. (рис.4.14);
(рис.4.14);
 – волновой вектор отраженной волны. Во второй среде волна неоднородна и
– волновой вектор отраженной волны. Во второй среде волна неоднородна и  . (4.97)Тогда, как и при выводе формул Френеля:
. (4.97)Тогда, как и при выводе формул Френеля:  .(4.98)
.(4.98) перпендикулярен плоскостям постоянных фаз и характеризует направление прошедшей волны. Угол y называется вещественным углом преломления. Отношение
перпендикулярен плоскостям постоянных фаз и характеризует направление прошедшей волны. Угол y называется вещественным углом преломления. Отношение  зависит от угла падения (в отличие от диэлектриков).
зависит от угла падения (в отличие от диэлектриков). .(4.99)
.(4.99) (4.100)В общем случае
(4.100)В общем случае  . При линейной поляризации падающего света с произвольным азимутом в отраженной волне появляется сдвиг фаз, приводящий к эллиптической поляризации отраженного света. Отраженный свет остается линейно поляризованным, если: 1) падающий свет s– или p– поляризован; 2)
. При линейной поляризации падающего света с произвольным азимутом в отраженной волне появляется сдвиг фаз, приводящий к эллиптической поляризации отраженного света. Отраженный свет остается линейно поляризованным, если: 1) падающий свет s– или p– поляризован; 2)  ;3)
;3) 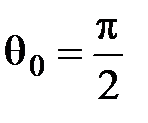 .
. ; (4.101)
; (4.101)  .(4.102)У металлов c2 значительно больше другого слагаемого. Поэтому
.(4.102)У металлов c2 значительно больше другого слагаемого. Поэтому  .Волновой вектор прошедшей в металл волны при нормальном падении имеет только z – составляющую:
.Волновой вектор прошедшей в металл волны при нормальном падении имеет только z – составляющую: ;(4.103)
;(4.103) — глубина проникновения. (4.104)
— глубина проникновения. (4.104) , а
, а  .(4.105)
.(4.105) . (4.106)
. (4.106) ,(4.107)называемая законом Бугера, где a – линейный показатель поглощения. Другой вид закона Бугера (см. (4.104)):
,(4.107)называемая законом Бугера, где a – линейный показатель поглощения. Другой вид закона Бугера (см. (4.104)): ,(4.108)где l0 – длина волны света в вакууме.
,(4.108)где l0 – длина волны света в вакууме.
 – относительный коэффициент преломления и
– относительный коэффициент преломления и  . Тогда из (5.36) и (5.47) следует выражение для фокусного расстояния линзы через относительный коэффициент преломления и её геометрические параметры:
. Тогда из (5.36) и (5.47) следует выражение для фокусного расстояния линзы через относительный коэффициент преломления и её геометрические параметры: (5.55)
(5.55) (5.56)
(5.56) (5.57)
(5.57) (5.58)называется оптической силой линзы. Оптическая сила измеряется в диоптриях (1 дптр соответствует фокусному расстоянию в 1 м). Оптическая сила положительна для собирающих линз и отрицательна для рассеивающих.
(5.58)называется оптической силой линзы. Оптическая сила измеряется в диоптриях (1 дптр соответствует фокусному расстоянию в 1 м). Оптическая сила положительна для собирающих линз и отрицательна для рассеивающих.
 (6.12)
(6.12) (что обычно реализуется в эксперименте) получаем:
(что обычно реализуется в эксперименте) получаем:
 имеем:
имеем:  .(6.14)Разность фаз между волнами в точке наблюдения при этом равна:
.(6.14)Разность фаз между волнами в точке наблюдения при этом равна: (6.15). Интерференционная картина на экране в зависимости от координаты y принимает вид:
(6.15). Интерференционная картина на экране в зависимости от координаты y принимает вид: 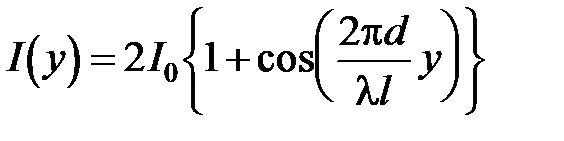 (6.16)
(6.16) Разумеется, приведенный расчет весьма приблизительный, т.к. кроме используемого приближения мы не учитывали размеры отверстия, а в их пределах фаза может существенно изменяться. Если же размеры меньше длины волны, то необходимо учитывать дифракционные эффекты.
Разумеется, приведенный расчет весьма приблизительный, т.к. кроме используемого приближения мы не учитывали размеры отверстия, а в их пределах фаза может существенно изменяться. Если же размеры меньше длины волны, то необходимо учитывать дифракционные эффекты.
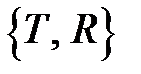 – амплитудные коэффициенты пропускания и отражения при входе волны внутрь пластины,
– амплитудные коэффициенты пропускания и отражения при входе волны внутрь пластины,  – амплитудные коэффициенты пропускания и отражения на выходе волны из пластины наружу.
– амплитудные коэффициенты пропускания и отражения на выходе волны из пластины наружу. При этом справедливы соотношения:
При этом справедливы соотношения: (6.30)
(6.30) , (6.31)
, (6.31) (6.32)
(6.32) .(6.33)
.(6.33) или
или  (6.34)
(6.34) При минимуме прошедшей проинтерферировавшей волны наблюдается максимальное отражение света от интерферометра тоже за счет интерференционного сложения волн на зеркалах.
При минимуме прошедшей проинтерферировавшей волны наблюдается максимальное отражение света от интерферометра тоже за счет интерференционного сложения волн на зеркалах. , где видна интерференционная картина. Оптимальное место для этого – центр картины (точка А), т.к. частотная дисперсия
, где видна интерференционная картина. Оптимальное место для этого – центр картины (точка А), т.к. частотная дисперсия  в этой точке максимальна. Поэтому конечность размеров фотоприемника минимально ухудшает разрешение ИФП как раз при таком местоположении. Теперь допустим, что одна из пластин ИФП параллельно перемещается вдоль оптической оси системы с постоянной скоростью v, т.е. h=h0+ v t. Тогда пропускание ИФП становится зависимым от времени, повторяя зависимость функции Эйри. Если на ИФП падает монохроматическая волна, то на осциллографе, развертка которого движется синхронно с пластиной, сигнал от ИФП опишет его аппаратную функцию в соответствии с (6.34). При сложном спектре электрический сигнал опишет исследуемый спектр. На практике перемещение пластин осуществляется или изменением давления газа между пластинами ИФП, или креплением одной из пластин на пьезокерамику. Второй способ предпочтительней, т.к. позволяет осуществить сканирование величины h(t) электрическим сигналом.
в этой точке максимальна. Поэтому конечность размеров фотоприемника минимально ухудшает разрешение ИФП как раз при таком местоположении. Теперь допустим, что одна из пластин ИФП параллельно перемещается вдоль оптической оси системы с постоянной скоростью v, т.е. h=h0+ v t. Тогда пропускание ИФП становится зависимым от времени, повторяя зависимость функции Эйри. Если на ИФП падает монохроматическая волна, то на осциллографе, развертка которого движется синхронно с пластиной, сигнал от ИФП опишет его аппаратную функцию в соответствии с (6.34). При сложном спектре электрический сигнал опишет исследуемый спектр. На практике перемещение пластин осуществляется или изменением давления газа между пластинами ИФП, или креплением одной из пластин на пьезокерамику. Второй способ предпочтительней, т.к. позволяет осуществить сканирование величины h(t) электрическим сигналом. Участок dx, находящийся на расстоянии x от левого края щели (начала координат), в направлении Z’ излучает плоскую волну с запаздыванием фазы относительно точки О на kx× sinj. Угол j отсчитывается от оси Z – нормали к щели (первоначального направления падающей волны), k – волновое число падающей волны. При записи амплитуды волны учтем, что вся щель в направлении j = 0 посылает излучение с амплитудой E0. Предполагая равномерное распределение амплитуды по щели, получим, что участок dx щели пошлет в направлении Z’ волну d E1 с амплитудой E0 d x / b:
Участок dx, находящийся на расстоянии x от левого края щели (начала координат), в направлении Z’ излучает плоскую волну с запаздыванием фазы относительно точки О на kx× sinj. Угол j отсчитывается от оси Z – нормали к щели (первоначального направления падающей волны), k – волновое число падающей волны. При записи амплитуды волны учтем, что вся щель в направлении j = 0 посылает излучение с амплитудой E0. Предполагая равномерное распределение амплитуды по щели, получим, что участок dx щели пошлет в направлении Z’ волну d E1 с амплитудой E0 d x / b:  (7.39) Отсюда имеем для амплитуды волны от всей щели:
(7.39) Отсюда имеем для амплитуды волны от всей щели:  (7.40)
(7.40) (7.41) где I0 = E02; I1 = E12;
(7.41) где I0 = E02; I1 = E12;  . (7.42)
. (7.42) , получаем, что в центре дифракционной картины интенсивность максимальна и равна I0.
, получаем, что в центре дифракционной картины интенсивность максимальна и равна I0. (7.43)
(7.43)
 . Возникновение двойного лучепреломления в жидкостях и аморфных прозрачных телах под воздействием электрического поля было открыто Керром в 1875г. (эффект Керра) и нашло широкое применение в практической деятельности.
. Возникновение двойного лучепреломления в жидкостях и аморфных прозрачных телах под воздействием электрического поля было открыто Керром в 1875г. (эффект Керра) и нашло широкое применение в практической деятельности. Между двумя скрещенными поляризаторами П1и П2 , плоскость пропускания каждого из которых составляет угол
Между двумя скрещенными поляризаторами П1и П2 , плоскость пропускания каждого из которых составляет угол  с вертикалью, помещена ячейка Керра – исследуемая жидкость в кювете между горизонтальными обкладками конденсатора, на которые подается электрическое напряжение.
с вертикалью, помещена ячейка Керра – исследуемая жидкость в кювете между горизонтальными обкладками конденсатора, на которые подается электрическое напряжение.


