
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоская электромагнитная волна, ее структура и представление в комплексной форме.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для анализа структуры плоской ЭМВ воспользуемся записью уравнений Максвелла с помощью определения и свойств оператора Гамильтона (набла-оператора):
Тогда уравнения Максвелла примут вид: Решение этих уравнений ищем в виде:
где E 0 и B 0 – постоянные векторы, не зависящие от координат и времени (в общем случае компоненты этих векторов могут быть комплексными). Учитывая, что (2.43) Максвелла Из этих соотношений можно сделать следующие выводы: 1. Плоская ЭМВ является поперечной. E, B и k составляют тройку взаимно перпендикулярных векторов. Поперечность световых колебаний была открыта в 1817 г. Юнгом 2. E =cB. 3. Т.к. k, w, m0, e0 – вещественные величины, то это значит, что E и B в плоской ЭМВ колеблются в одинаковой фазе.
Сферические волны. Сходящиеся и расходящиеся сферические волны.
Рассмотрим изотропную волну от точечного источника. Тогда решение уравнения (2.10) будем искать в виде Ф(r,t), где r – расстояние от точечного источника. В сферической системе координат (r, q, j):
Плотность потока энергии и импульса световых волн. Давление света. Плотность потока энергии электромагнитных волн определяется вектором Пойнтинга:
Плотность импульса электромагнитной волны. ЭМВ обладает не только энергией, но и импульсом. В курсе “Электричество” было показано, что плотность импульса G ЭМВ связана с плотностью потока энергии S в ней соотношением: Давление света. Идея о давлении света была высказана еще Кеплером для объяснения отклонения хвостов комет от Солнца во время их прохождения вблизи его. Действительно, если при отражении света меняется его импульс, то на тело воздействует соответствующая сила, т.е. возникает световое давление. Первый достоверный опыт по обнаружению светового давления провел выдающийся отечественный физик-экспериментатор П.Н. Лебедев в 1900 г. Если ЭМВ падает нормально на плоскую поверхность и полностью поглощается, то световое давление откуда Видно, что если поверхность, на которую направляется ЭМВ полностью отражающая, то давление света на нее в два раза больше, чем на полностью поглощающую поверхность.
5. Суперпозиция электромагнитных волн. Стоячие волны. Биения. Суперпозиция ЭМВ. Напряженность электрического поля и магнитная индукция равны соответственно сумме напряженностей и магнитных индукций всех полей в данной точке независимо от их происхождения, частоты и направления распространения. Однако полученная в результате сложения полей совокупность электромагнитных полей, вообще говоря, не составляет бегущую электромагнитную волну. Суперпозиция бегущих плоских монохроматичных ЭМВ. Пусть заданы две волны, для которых k1 = k2 = k, w1 = w2 = w и
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 866; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.102.112 (0.009 с.) |

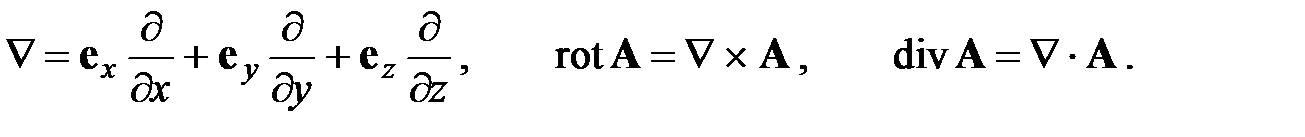

 (2.41)
(2.41) (2.42)
(2.42)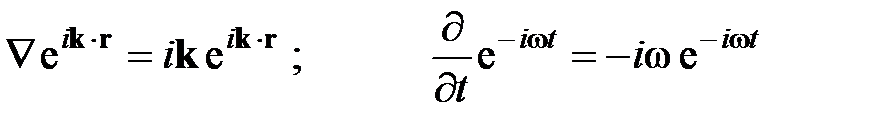 и подставляя решения (2.41) и (2.42) в уравнения
и подставляя решения (2.41) и (2.42) в уравнения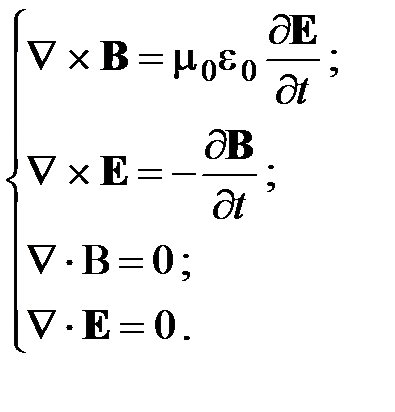 , получаем следующие важные соотношения, описывающие структуру плоской ЭМВ:
, получаем следующие важные соотношения, описывающие структуру плоской ЭМВ: 
 (2.10)
(2.10) (2.21) а искомое решение из соображений симметрии не зависит от угловых координат. Тогда волновое уравнение примет вид:
(2.21) а искомое решение из соображений симметрии не зависит от угловых координат. Тогда волновое уравнение примет вид: (2.22) т.е. имеет вид (2.11), если произвести замену z® r, Ф®rФ. Тогда общее решение уравнения (2.22) имеет вид:
(2.22) т.е. имеет вид (2.11), если произвести замену z® r, Ф®rФ. Тогда общее решение уравнения (2.22) имеет вид:  (2.23) Выясним физический смысл полученного решения. Второе слагаемое представляет собой волну, движущуюся в направлении увеличения значений r, т.е. от центра (точечного источника). Такая волна называется расходящейся. Первое слагаемое описывает волну, движущуюся в направлении уменьшения r, т.е. к центру. Такая волна называется сходящейся. Общее решение является суперпозицией сходящейся и расходящейся волн. Значение Ф в фиксированный момент времени на сфере постоянного радиуса является постоянным. Такие волны называются сферическими.
(2.23) Выясним физический смысл полученного решения. Второе слагаемое представляет собой волну, движущуюся в направлении увеличения значений r, т.е. от центра (точечного источника). Такая волна называется расходящейся. Первое слагаемое описывает волну, движущуюся в направлении уменьшения r, т.е. к центру. Такая волна называется сходящейся. Общее решение является суперпозицией сходящейся и расходящейся волн. Значение Ф в фиксированный момент времени на сфере постоянного радиуса является постоянным. Такие волны называются сферическими. (2.49). В случае плоской волны модуль вектора Пойнтинга может быть представлен в виде:
(2.49). В случае плоской волны модуль вектора Пойнтинга может быть представлен в виде:  (2.50). При характерных для оптического диапазона высоких частотах w (» 1015 с-1) колебания потока энергии волны в каждой точке, происходящие в соответствии с (2.50) на частоте 2w, не наблюдаемы и физический интерес представляет лишь среднее по времени значение S, называемое обычно интенсивностью света. Учитывая, что E = E0 cosw t, где E0 – амплитуда напряженности электрического поля, находим для интенсивности световой волны:
(2.50). При характерных для оптического диапазона высоких частотах w (» 1015 с-1) колебания потока энергии волны в каждой точке, происходящие в соответствии с (2.50) на частоте 2w, не наблюдаемы и физический интерес представляет лишь среднее по времени значение S, называемое обычно интенсивностью света. Учитывая, что E = E0 cosw t, где E0 – амплитуда напряженности электрического поля, находим для интенсивности световой волны: 

 ,, т.к. за 1 с на 1 м2 передается импульс G. Если поглощение частичное, а остальное отражается и a – коэффициент поглощения, то S погл = a S и по закону сохранения энергии S отр = (1– a) S, тогда
,, т.к. за 1 с на 1 м2 передается импульс G. Если поглощение частичное, а остальное отражается и a – коэффициент поглощения, то S погл = a S и по закону сохранения энергии S отр = (1– a) S, тогда 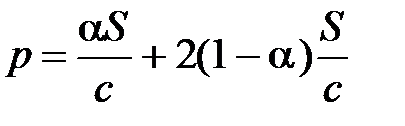
 .
.
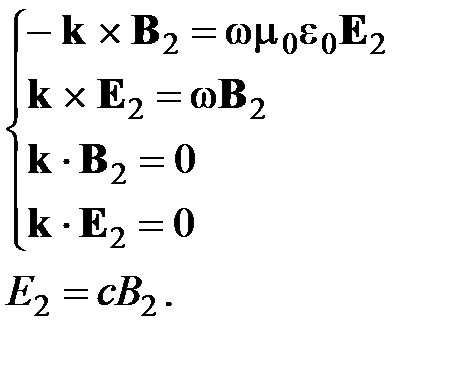 2.55 2.56
2.55 2.56


