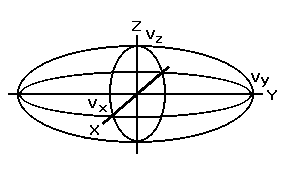Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анизотропные среды. Тензор диэлектрической проницаемости. Распространение плоской электромагнитной волны в анизотропной среде. Эллипсоид лучевых скоростей.Содержание книги
Поиск на нашем сайте
Оптической анизотропией называется зависимость опт.св-в среды от напр-ияраспро-ия света в ней. Физич. природа анизотропии вещества связана с особенностями строения его молекул или особенностями кристаллич. решетки, в узлах к-ой нах-ся атомы или ионы. Изучение распр-ия света в анизотроп. средах мы будем строить с помощью феноменологической электромагн. теории. В рамках этой теории анизотропия учит-ся тем, что в материальном уравнении диэлектрическая восприимчивостьc(w) представляет собой тензор, а не скаляр, как для изотроп.среды. В анизотропной среде проекции поляризованности связаны с проекциями напряженности электрического поля соотношениями:
В дальнейшем для простоты будем нумеровать декартовы оси координати соответствующие им проекции числами или индексами 1, 2, 3. Матрица величин cij называется тензором диэлектрической восприимчивости. Тогда системуможно записать в компактном виде: Т.к. проекции поля E независимы, то тензор диэлектрической проницаемости является симметричным: Воспользуемся математическими свойствами полученных выражений. Т.к. плотность электрической энергии положительна, то стоящая в правой части (9.5) квадратичная форма является положительно определенной.Перейдя к новым переменным: В главных осях соотношение (9.3) примет вид: Т.к. в общем случае элементы тензора диэлектрической проницаемости неодинаковы, то в анизотропной среде векторы D и E не коллинеарны. Распространение плоской электромагнитной волны в анизотропной среде. Подставляя векторы E, D, H, B в плоской ЭМВ в виде
Волновой вектор k показывает направление распр-ие вол-го фронта, т.е. фазовая скорость v направлена вдоль вол-го вектора. Введем единич. вектор напр-ияраспр-ия волны n: Т.к. а анизотропной среде векторы E и D не коллинеарны, то направления распространения волны и луча не совпадают. Соответственно не совпадают по направлению групповая и фазовая скорость. Ориентация между векторами в ЭМВ изображена на рис. 9.1. Вектора D, E, n, t лежат в одной плоскости, перпендикулярной H, n ^ D; t ^ E. Угол между D и E равен углу между n и t. Вектор E, оставаясь перпендикулярным H, не перп-н напр-июраспр-ия фазы волны. В этом смысле волна в кристалле не яв-ся строго поперечной, т.к. имеется отличная от нуля проекция вектора E на напр-ие n и соот-о проекция D на напр-ие t. Лишь при ориентации вдоль одной из главных осей кристалла вектор D коллинеарен вектору E. Пл-ть равных фаз перемещается вдоль вектора n со скоростью v. Скорость перемещения этой плоскости вдоль вектора луча t называется лучевой скоростью.
Особенности распр-ия лучей в анизотропной среде обусловлены как дисперсией волн, так и отличием направлений волновых нормалей и лучей. Дисперсия в равной мере присуща как изотропным, так и анизотропным средам. Но чтобы выделить особенности анизотропии, в дальнейшем будем пренебрегать дисперсией. В такой недиспергирующей анизотропной среде понятия лучевой скорости и групповой скорости совпадают. Получим выражение для зависимости фазовой скорости от направления распр-ия волны и пл-ти поляризации. Здесь ni – направляющие косинусы направления волны относительно соответствующей главной оси. Пусть E направлен, например, вдоль гл. оси X. Тогда система сводится к одному уравнению При ненулевом поле E получаем:
Полученные скорости vi называются главными скоростями распространения волны. Необходимо отметить, что: · vi – это не проекции вектора фазовой скорости на соответствующую главную ось, а фазовые скорости волны, у которой векторы E и D коллинеарны соответствующей главной оси; · Главные лучевые (групповые) скорости совпадают с главными фазовыми скоростями. Ход лучей в анизотропной среде. Исходя из определения, лучевая (групповая) скорость u и фазовая скорость v в анизотропной среде связаны соотношением: Так же как и для случая фазовых скоростей, две волны (луча), распространяющихся в данном направлении с двумя лучевыми скоростями, имеют взаимно перпендикулярные направления поляризации. Обычно для решения одних задач по анизотропным средам удобнее работать с фазовыми скоростями, для других с лучевыми скоростями. Произведя замену Проанализируем ход лучей с помощью эллипсоида лучевых скоростей. Направление луча задается единичным вектором t. Через центр эллипсоида проведем плоскость, перпендикулярную t. В сечении эллипсоида этой плоскостью образуется эллипс с главными полуосями v1, v2. Вектор E световой волны, распространяющейся по лучу, может колебаться только параллельно главным осям этого эллипса. Соответствующие лучевые скорости равны длинам его главных полуосей. В направлении, перпендикулярном плоскости кругового сечения, всем лучам соответствует одна и та же скорость, поляризация может быть любой.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 504; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.41.80 (0.006 с.) |

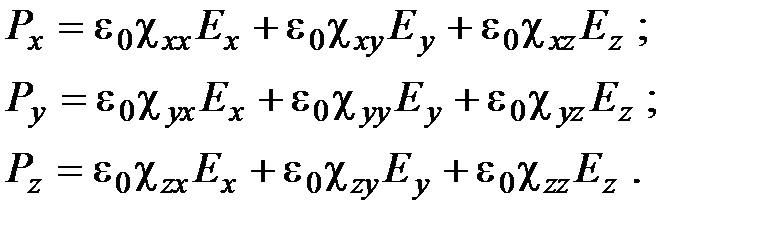
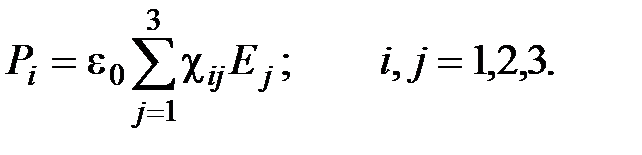 Соотношение между компонентами вектора электрического смещения D и поляризованностью P для анизотропной среды принимает вид:
Соотношение между компонентами вектора электрического смещения D и поляризованностью P для анизотропной среды принимает вид: 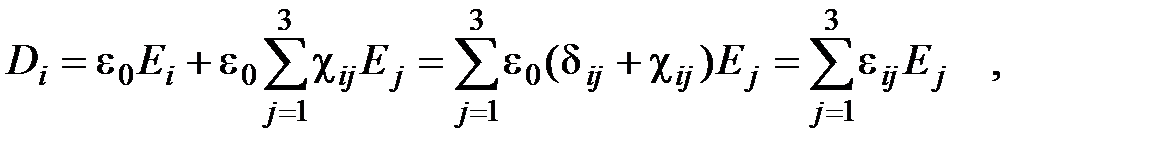 где dij – символ Кронекера. Тензор eij:
где dij – символ Кронекера. Тензор eij: 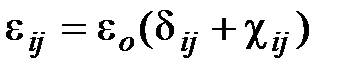 (называется тензором диэлектрической проницаемости.
(называется тензором диэлектрической проницаемости.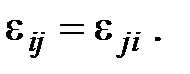
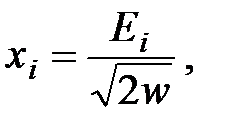 выражение можно записать в виде:
выражение можно записать в виде: 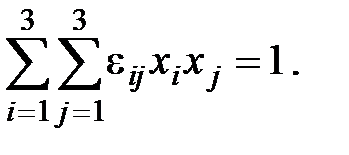 Как известно из математики, с помощью преобразования системы координат такая форма может быть приведена к виду:
Как известно из математики, с помощью преобразования системы координат такая форма может быть приведена к виду: 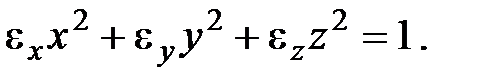 Полученные таким образом оси X, Y, Zновой системы координат называют главными осями тензора диэлектрической проницаемости (в дальнейшем мы их так и будем обозначать большими буквами). В главной системе координат тензор диэлектрической проницаемости является диагональным:
Полученные таким образом оси X, Y, Zновой системы координат называют главными осями тензора диэлектрической проницаемости (в дальнейшем мы их так и будем обозначать большими буквами). В главной системе координат тензор диэлектрической проницаемости является диагональным: 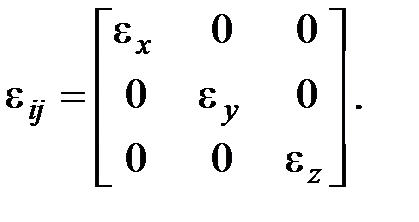
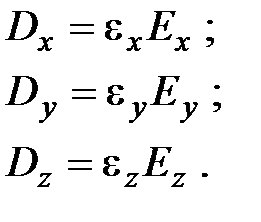
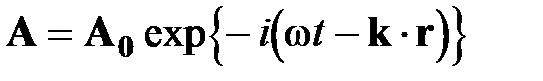 в уравнения Максвелла, получим следующие соотношения между векторами полей и волновым вектором k:
в уравнения Максвелла, получим следующие соотношения между векторами полей и волновым вектором k: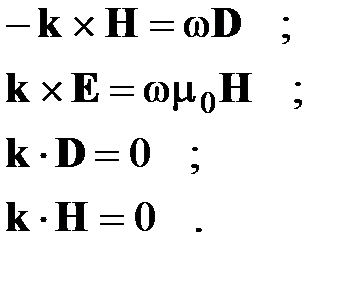
 Поток энергии, по определению, распространяется по направлению вектора Пойнтинга S = E ´ H. Направление потока энергии в волне называется лучом. Т.к. энергия ЭМВ распространяется с групповой скоростью, то групповая скорость u направлена вдоль луча. Введем единичный вектор в направлении распространения луча: τ= S/ S
Поток энергии, по определению, распространяется по направлению вектора Пойнтинга S = E ´ H. Направление потока энергии в волне называется лучом. Т.к. энергия ЭМВ распространяется с групповой скоростью, то групповая скорость u направлена вдоль луча. Введем единичный вектор в направлении распространения луча: τ= S/ S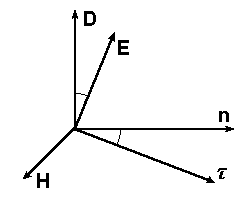
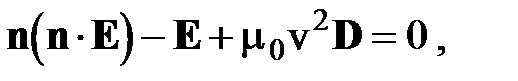 где v = w/ k – фазовая скорость. В главной системе координат с учетом в скалярном виде преобразуется в систему трех уравнений:
где v = w/ k – фазовая скорость. В главной системе координат с учетом в скалярном виде преобразуется в систему трех уравнений: 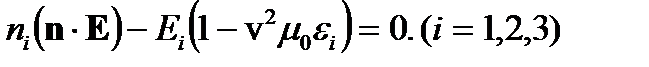
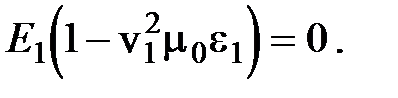
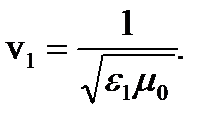 Аналогичные рассмотрения случаев, когда E (и соответственно D) направлено или вдоль Y или вдоль Z, позволяют найти остальные значения vi:
Аналогичные рассмотрения случаев, когда E (и соответственно D) направлено или вдоль Y или вдоль Z, позволяют найти остальные значения vi: 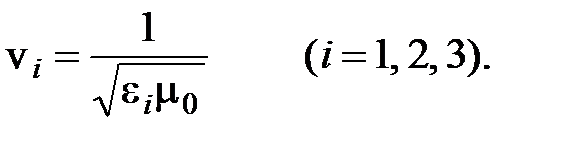
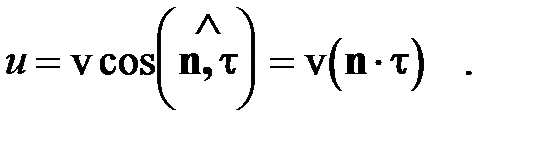 Аналогично можно уравнение Френеля для лучевых скоростей:
Аналогично можно уравнение Френеля для лучевых скоростей: 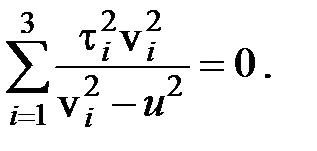
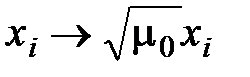 , получим уравнение:
, получим уравнение: 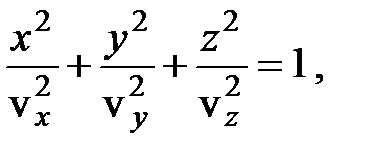 где vx, vy, vz – главные лучевые скорости. Эллипсоид, точки поверхности которого удовлетворяют уравнению называется эллипсоидом лучевых скоростей (координаты имеют размерность скоростей).
где vx, vy, vz – главные лучевые скорости. Эллипсоид, точки поверхности которого удовлетворяют уравнению называется эллипсоидом лучевых скоростей (координаты имеют размерность скоростей).