
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип Гюйгенса-Френеля. Зоны Френеля. Графическое вычисление амплитуды. Пятно Пуассона и пятно Араго.Содержание книги
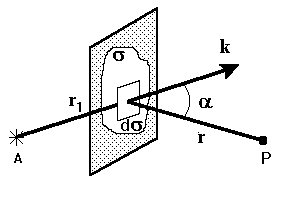
Поиск на нашем сайте Под дифракцией света обычно понимают отклонения закономерностей распространения света от законов, предписываемых геометрической оптикой. В явлениях дифракции, как и в интерференции, проявляются волновые свойства света. Дифракцию можно наблюдать, например, когда на пути распространения света находятся препятствия, т.е. непрозрачные тела произвольной формы (экраны) и свет проходит сквозь отверстия в экранах или когда волновой фронт искусственно ограничен. Тщательный опыт показывает, что вместо резкой границы между светом и тенью (как предсказывает геометрическая оптика) получается сложная картина распределения освещенности, состоящая из темных и светлых участков – дифракционных полос. Теория дифракции света дает строгое обоснование геометрической оптике и определяет условия ее применимости. Математически строгое решение дифракционных задач на основе волнового уравнения (или уравнений Максвелла) с граничными условиями, зависящими от характера препятствий, как правило, представляет значительные трудности. Поэтому чаще всего применяются приближенные методы решения задачи о распределении света вблизи границы между светом и тенью, основанные на принципе Гюйгенса – Френеля. Пусть A – источник света, а s – произвольная замкнутая поверхность, охватывающая A (рис.7.1).
Принцип Гюйгенса – Френеля: в любой точке, находящейся вне поверхности s, световая волна, возбуждаемая источником A, может быть представлена как результат суперпозиции когерентных вторичных волн, которые “излучаются” элементарными воображаемыми источниками, непрерывно распределенными вдоль вспомогательной поверхности s. Иными словами, вне поверхности s действительно распространяющаяся (первичная) волна может быть заменена системой когерентных фиктивных вторичных волн, интерферирующих при наложении. Рассмотрим экран с некоторым отверстием, через которое проходит свет от данного источника A. Проведем мысленно произвольную поверхность s, закрывающую отверстие в экране и ограниченную краями отверстия. Разделим эту поверхность на элементарные участки площадью ds, малые по сравнению с размерами отверстия, но большие по сравнению с длиной волны. Каждый из этих участков сам становится источником вторичных волн, распространяющихся во все стороны. Пусть E (r 1) – напряженность поля в самом участке ds. Напряженность поля d E p, создаваемая элементарным участком ds в точке наблюдения P определяется формулой:
где K (a) – некоторый коэффициент, учитывающий зависимость амплитуды вторичных волн от угла a между вектором k и направлением на точку наблюдения. Полное поле в точке P представляет собой суперпозицию полей (7.1) от всех элементов ds поверхности, закрывающей отверстие в экране:
Эта формула дает математическое выражение принципа Гюйгенса – Френеля. Зоны Френеля. Пусть сферическая волна падает на непрозрачный экран с отверстием. Требуется найти распределение интенсивности света за экраном. Для решения этой задачи делаются два предположения: 1) непроницаемые части экрана не являются источниками вторичных волн; 2) в отверстии точки волнового фронта являются такими же источниками вторичных волн, какими они были бы при отсутствии непроницаемых частей экрана. Пусть A – источник сферической волны, S – волновой фронт в некоторый момент времени, R – радиус кривизны этого фронта (рис.7.2).
Из геометрии рис.7.3 можно получить для радиуса m –й зоны Френеля rm:
Исключая величину d m и пренебрегая слагаемыми ~l2 ввиду их малости, получаем:
Площади всех зон Френеля примерно одинаковы (в случае пренебрежения кривизной поверхности, что не вносит существенной ошибки, если радиусы зон Френеля много меньше радиуса кривизны волнового фронта (обычно это справедливо для очень большого числа зон Френеля)): Графическое вычисление амплитуды (метод векторных диаграмм). Разделим каждую из зон на большое число N участков. Между началом и концом зоны фаза меняется наp, а между малыми участками – на d = p/ N. Пусть E 0 – амплитуда волны, приходящей в точку наблюдения P от каждого участка; а фаза волны, приходящей из точки D в точку P – равна нулю. Комплексная амплитуда волны в точке P от центральной зоны Френеля с учетом интерференции равна: Аналитическое сложение амплитуд можно проделать графически, изображая комплексную амплитуду в виде вектора (рис.7.3).
Пятно Пуассона. Если на пути световой волны стоит непрозрачный круглый экран, то за экраном в его тени на оси возникает светлое пятно, называемое пятном Пуассона. Необходимость возникновения светлого пятна очевидна из рассуждений по методу зон Френеля. Экран закрывает некоторое число зон Френеля начиная с центральной. Однако следующие зоны после последней из закрытых создают в точке P освещенность, значение которой можно рассчитать с помощью спирали. Т.о., получается, что волна как бы огибает непрозрачный экран. Интенсивность пятна Пуассона весьма слаба при больших размерах непрозрачного экрана. Кроме того, необходимо, чтобы свет обладал достаточно большой степенью когерентности. Отметим, что можно наблюдать и противоположный эффект – темное пятно в центре картинки при дифракции на открытом отверстии. Такое пятно называется пятном Араго.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1072; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.86.133 (0.007 с.) |

 (7.1)
(7.1)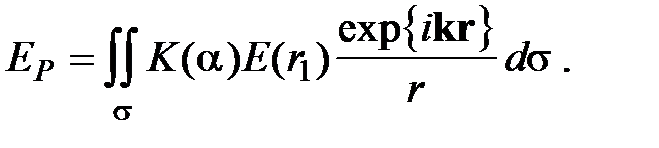 (7.2)
(7.2)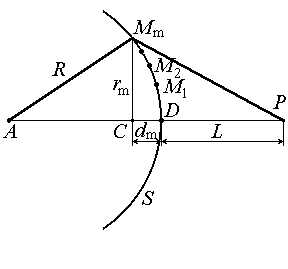 Найдем интенсивность в точке P с помощью принципа Гюйгенса – Френеля. Разобьем поверхность S на кольцеобразные зоны такого размера, чтобы расстояния от краев зоны (в разрезе это соответствует точкам M 1, M 2, M 3 , …) до P отличались на l/2 (эти зоны называются зонами Френеля):
Найдем интенсивность в точке P с помощью принципа Гюйгенса – Френеля. Разобьем поверхность S на кольцеобразные зоны такого размера, чтобы расстояния от краев зоны (в разрезе это соответствует точкам M 1, M 2, M 3 , …) до P отличались на l/2 (эти зоны называются зонами Френеля):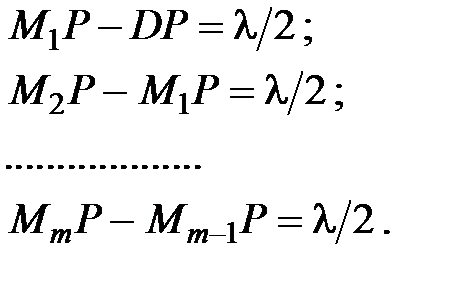 (7.3)
(7.3) (7.4)
(7.4)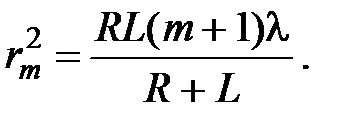 (7.5)
(7.5) (7.6)
(7.6)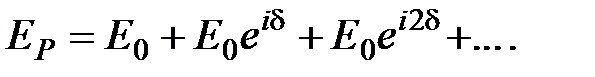 (7.7)
(7.7)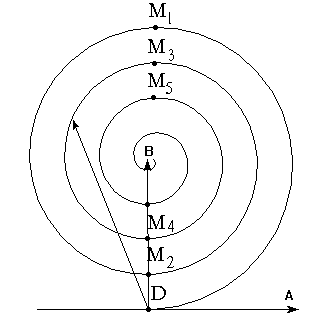 При увеличении числа разбиений до бесконечности ломаная кривая превращается в плавную. Длина вектора DM 1 пропорциональна амплитуде волны в точке P, когда открыта вся центральная зона Френеля. Аналогично продолжая построение, можно получить кривую, по которой легко определить амплитуду волны (и ее интенсивность), зная соотношение диаметров открываемого отверстия и зон Френеля. При строгом равенстве амплитуд в (7.7) складываемых колебаний от элементарных участков результирующая амплитуда от двух открытых соседних зон была бы равна нулю, т.е. вторичные волны в результате интерференции гаси ли бы друг друга, но коэффициент наклона K (a) в (7.1) убывает по мере увеличения a и приводит к уменьшению амплитуд вторичных волн. Поэтому полученная кривая не замыкается, а имеет вид спирали. Зависимость амплитуды поля в точке P от радиуса отверстия показана на рис.7.4.
При увеличении числа разбиений до бесконечности ломаная кривая превращается в плавную. Длина вектора DM 1 пропорциональна амплитуде волны в точке P, когда открыта вся центральная зона Френеля. Аналогично продолжая построение, можно получить кривую, по которой легко определить амплитуду волны (и ее интенсивность), зная соотношение диаметров открываемого отверстия и зон Френеля. При строгом равенстве амплитуд в (7.7) складываемых колебаний от элементарных участков результирующая амплитуда от двух открытых соседних зон была бы равна нулю, т.е. вторичные волны в результате интерференции гаси ли бы друг друга, но коэффициент наклона K (a) в (7.1) убывает по мере увеличения a и приводит к уменьшению амплитуд вторичных волн. Поэтому полученная кривая не замыкается, а имеет вид спирали. Зависимость амплитуды поля в точке P от радиуса отверстия показана на рис.7.4.



