
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерференция света. Условия наблюдения линий максимальной и минимальной интенсивности. Видность интерференционной картины. Временная и пространственная когерентности света.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Интерференцией называется изменение средней плотности потока энергии, обусловленное суперпозицией электромагн. волн. В дальнейшем под интенсивностью световой монохроматической волны будем понимать следующую величину, определяемую формулой:
С учетом (6.1) и (6.2) выражение (6.3) принимает вид:
где Если частоты интерферирующих волн различны, то формула (6.4) примет вид:
Последнее слагаемое в (6.4) или в (6.5) называется интерференционным членом. В тех случаях, когда он обращается в нуль, результирующая интенсивность равна сумме интенсивностей отдельных волн и интерференция отсутствует. Если же интерференционный член отличен от нуля, то суммарная интенсивность изменяется от минимального значения
до максимального значения
На практ. для количеств. хар-ки качества интерф. картины вводят понятие ее функции видности:
Допустим, что наша волна имеет следующую временную зависимость
ti – средние времена смены фазы колебания амплитуды. Величина Временная и пространственная когерентность. Для возникновения интерференции необходимо, чтобы разность фаз между интерферирующими волнами сохраняла свое значение за время усреднения. Поэтому и вводят понятие когерентных колебаний, для которых разность фаз за время наблюдения остается неизменной. При описании интерференционных явлений часто используют понятия временной и пространственной когерентности. Временную когерентность связывают со степенью монохроматичности волн, а пространственную когерентность – с геометрией эксперимента.
Двулучевая интерференция, осуществляемая делением амплитуды. Интерферометр Майкельсона. Интерферометр Майкельсона. Интерферометр состоит из делительной пластинки P и двух зеркал R 1и R 2, расположенных на расстояниях l 1 и l 1 от пластины (рис.6.1).
На пластинке P происходит деление амплитуды, поскольку фронты волн на ней сохраняются, меняя лишь направление своего движения. Нетрудно показать, что при любом коэффициенте отражения света от пластинки амплитуды полей, приходящих в точку наблюдения А одинаковы. Т.к. частоты также остаются постоянными, то (6.5) принимает вид: При этом интенсивность I изменяется от своего минимального значения при Пример применения интерферометра Майкельсона. При движении одного из зеркал за счет продольного эффекта Доплера происходит смещение частоты отраженной волны: Тогда существенной станет не постоянная амплитуда, а периодически изменяющаяся с частотой в соответствии со значением скорости движения зеркала: Как видно, интерферометр Майкельсона – прекрасный инструмент не только для измерений расстояний, но и скорости перемещения объектов, т.к. он весьма чувствителен к перемещениям. Поставив в одно из плеч призму или линзу, можно получить великолепный инструмент для исследования их качества по интерференционной картине (интерферометр Тваймана–Грина). Другой пример интерферометра по методу деления амплитуды – интерферометр Маха–Цендера (рис.6.2).
По изменению интерференционной картины и длине пути светового пучка в ячейке Q можно с большой точностью определить относительный показатель преломления исследуемого вещества ячейки. Двулучевая интерференция, осуществляемая делением волнового фронта. Схема Юнга. Примеры практических схем двулучевой интерференции. Многие оптические двух лучевые интерференционные схемы могут быть сведены к идеализированной схеме. Конечно, в реальных схемах используются не два, а один источник света, но лучи от этого источника попадают на экран, где наблюдается интерференция, по двум различным путям. Расщепление первоначальной волны от источника на две и последующее их сведение на экране — общий признак всех двухлучевых интерференционных схем. Опыт Юнга (1801 г.). Рассмотрим интерференцию, возникающую в результате выделения с помощью двух щелей S 1и S 2 участков сферического волнового фронта волны от точечного источника S (рис.6.3) (метод деления волнового фронта).
Найдем разность хода лучей в произвольной точке наблюдения P на экране:
При
(6.13) Следовательно, с точностью до величины первого порядка по
Примеры экспериментальных интерференционных схем, осуществляющих метод деления волнового фронта: бипризма Френеля, билинза Бийе, бизеркало Френеля, зеркало Ллойда.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.5.179 (0.009 с.) |

 (6.1) где E 0 – действительная амплитуда световой волны. Рассмотрим суперпозицию двух линейно поляризованных в одном направлении волн с различными амплитудами:(6.2)
(6.1) где E 0 – действительная амплитуда световой волны. Рассмотрим суперпозицию двух линейно поляризованных в одном направлении волн с различными амплитудами:(6.2)  Тогда суммарная интенсивность I будет равна: (6.3)
Тогда суммарная интенсивность I будет равна: (6.3)
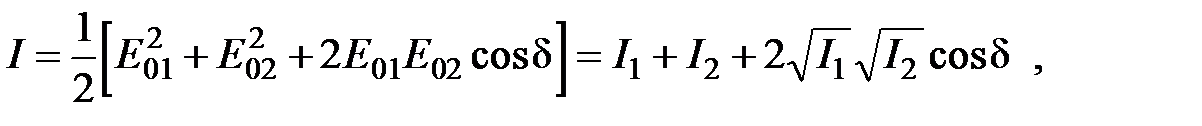 (6.4)
(6.4)
 (6.5)
(6.5)

 (6.22) где
(6.22) где  – экспер-но опред. величины в точке набл.:
– экспер-но опред. величины в точке набл.:

 является характерным временным масштабом случайных флуктуаций фазы световой волны и называется временем когерентности.
является характерным временным масштабом случайных флуктуаций фазы световой волны и называется временем когерентности.
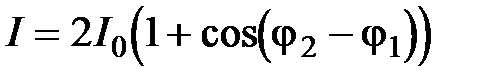 .(6.8)
.(6.8) до своего максимального значения при
до своего максимального значения при  . Значение разности фаз определяется длинами плеч интерферометра l 1 и l 2:
. Значение разности фаз определяется длинами плеч интерферометра l 1 и l 2:  .(6.9)
.(6.9) . (6.10)
. (6.10) .(6.11)
.(6.11)

 (6.12)
(6.12) (что обычно реализуется в эксперименте) получаем:
(что обычно реализуется в эксперименте) получаем:
 имеем:
имеем:  .(6.14)Разность фаз между волнами в точке наблюдения при этом равна:
.(6.14)Разность фаз между волнами в точке наблюдения при этом равна: (6.15). Интерференционная картина на экране в зависимости от координаты y принимает вид:
(6.15). Интерференционная картина на экране в зависимости от координаты y принимает вид: 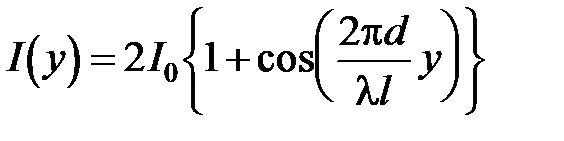 (6.16)
(6.16) Разумеется, приведенный расчет весьма приблизительный, т.к. кроме используемого приближения мы не учитывали размеры отверстия, а в их пределах фаза может существенно изменяться. Если же размеры меньше длины волны, то необходимо учитывать дифракционные эффекты.
Разумеется, приведенный расчет весьма приблизительный, т.к. кроме используемого приближения мы не учитывали размеры отверстия, а в их пределах фаза может существенно изменяться. Если же размеры меньше длины волны, то необходимо учитывать дифракционные эффекты.



