Распределение энергии при интерференции.

Наличие минимума в точке С означает: энергия W сюда не поступает.

Наличие максимума в точке С означает: происходит увеличе­ние за счет перераспределения энергии в пространстве. Так как энергия пропорциональна квадрату амплитуды, то при увели­чении амплитуды в 2 раза энергия увеличивается в 4 раза. Это означает, что в точку С поступает энергия в 4 раза боль­ше энергии одного вибратора при условии: энергии вибраторов равны.

Интерференция присуща волнам любой природы (механиче­ским, электромагнитным).

 

Необходимые условия для наблюдения интерференции:

1) волны должны иметь одинаковые (или близкие) частоты, чтобы картина, получающаяся в результате наложения волн, не менялась во времени (или менялась не очень быстро, что бы её можно было успеть зарегистрировать);

2) волны должны быть однонаправленными (или иметь близкое направление); две перпендикулярные волны никогда не дадут интерференции (попробуйте сложить две перпендикулярные синусоиды!). Иными словами, складываемые волны должны иметь одинаковые волновые векторы (или близконаправленные).

Волны, для которых выполняются эти два условия, называются КОГЕРЕНТНЫМИ. Первое условие иногда называют временной когерентностью, второе - пространственной когерентностью.

Условия наблюдения интерференции

Рассмотрим несколько характерных случаев:

1. Ортогональность поляризаций волн.

При этом и . Интерференционные полосы отсутствуют, а контраст равен 0. Далее, без потери общности, можно положить, что поляризации волн одинаковы.

2. В случае равенства частот волн и контраст полос не зависит от времени экспозиции .

3. В случае значение функции и интерференционная картина не наблюдается. Контраст полос, как и в случае ортогональных поляризаций, равен 0

4. В случае контраст полос существенным образом зависит от разности частот и времени экспозиции.

4.3

Максимум интерференционной картины будет наблюдаться при условии синфазного сложения колебаний волн источников, которое имеет место при . Исходя из связи между разностью фаз колебаний и оптической разностью хода , можно заключить, что синфазное сложение колебаний имеет место при условии кратности оптической разности хода целому числу длин волны в среде:

 

,

(4.8)

 

где - произвольное целое число, равное .

 

Найдём координату , определяющую положение - ого максимума интерференционной картины:

 

,

(4.9a)

 

где - длина волны в вакууме, связанная с длиной волны в среде распространения с помощью формулы .

 

Порядком интерференционного максимума называют его номер ' ', отсчитываемый от центрального (), которому соответствует центр интерференционной картины, где складываются волны от источников, проходящие одинаковый путь ().

 

Аналогичным образом можно найти положения минимумов интерференционной картины двух источников, определяемые координатами , если положить оптическую разность хода кратной нечётному числу полуволн:

 

.

(4.9b)

 

где - произвольное целое число, равное .

 

Отсюда следует, что в рассматриваемой интерференционной картине положения соседних интерференционных максимумов и минимумов находятся на одинаковом расстоянии друг от друга и не зависят от того, насколько эти максимумы удалены от центра интерференционной картины. Это свойство максимумов и минимумов позволяет определить ширину интерференционной полосы.

• Связь разности фаз Δφ колебаний с оптической разностью хо­да волн

Δφ=2πΔ/λ..

• Условие максимумов интенсивности света при интерферен­ции

Δ=±kλ (k=0,l,2,3, …).

• Условие минимумов интенсивности света при интерферен­ции

Δ=±(2k+1) (λ/2).

Примеры интерференции: двулучевая интерференция, интерференция при отражении от тонких пластинок, кольца Ньютона, многолучевая интерференция.

При наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других- минимумы интенсивности. Это явление называется интерференцией волн.

Двулучевая интерференция:

Под двулучевой интерференцией понимают интерференционную картину, возникающую при сложении двух световых волн одинаковой частоты. Расщепление первоначальной волны от источника на две и последующее их сведение на экране — общий признак всех двулучевых интерференционных схем.

Опыт Юнга:

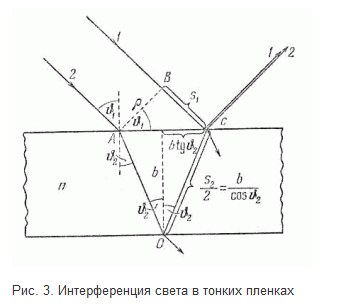
Схема 1 — опыт Юнга — первый опыт по наблюдению интерференции света, осуществленный в 1827 г. Источником света служит ярко освещенная щель S. Свет, прошедший через 5, падает на две узкие щели S1 и S2. Световые пучки, прошедшие через S1 и S2, уширяются вследствие дифракции. Интерференция наблюдается на экране в области перекрытия дифракционных пучков.

Интерференция при отражении от тонких пластинок:

При падении световой волны на тонкую прозрачную пластинку или пленку происходит отражение от обеих поверхностей пластинки. В результате возникают когерентные световые волны, которые могут интерферировать.

Пусть на прозрачную плоскопараллельную пластинку падает параллельный пучок света, представленный на рис. 3 только одним лучом. Пластинка отбрасывает вверх два когерентных параллельных пучка света, из которых один образуется за счет отражения от верхней поверхности пластинки, второй — вследствие отражения от нижней поверхности. При входе в пластинку и при выходе из нее второй пучок претерпевает преломление. Кррме этих двух пучков пластинка отбросит вверх пучки, возникающие 'в результате трех-, пяти- и т. д. кратного отражения от поверхностей пластинки.

Интерференция в плоскопараллельной пластине:

Схема 4 — интерференция в плоскопараллельной пластинке. В таблице изображен общий случай произвольного расположения источника и плоскости наблюдения по отношению к плоскопараллельной пластинке. Свет, приходящий в точку наблюдения Р, можно рассматривать как свет от двух мнимых изображений источника S в двух гранях пластинки. Интерференционная картина в пределах достаточно малой площади экрана состоит из почти параллельных интерференционных полос. Разность хода в данном интерференционном расположении есть:

Здесь h — толщина пластинки, n — показатель преломления, r — угол преломления. Дополнительное слагаемое λ/2 возникает из-за разных условий отражения света на двух гранях пластинки.

Кольца Ньютона:

Кольца Ньютона

Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла (рис. 8.13), называют кольцами Ньютона.

Общий центр колец расположен в точке касания. В отраженном свете центр темный, так как при толщине воздушной прослойки, на много меньшей, чем длина волны, разность фаз интерферирующих волн обусловлена различием в условиях отражения на двух поверхностях и близка к π. Толщина h воздушного зазора связана с расстоянием r до точки касания (рис. 8.13):

Здесь использовано условие . При наблюдении по нормали темные полосы, как уже отмечалось, соответствуют толщине , поэтому для радиуса m-го темного кольца получаем

(m = 0, 1, 2, …).

Если линзу постепенно отодвигать от поверхности стекла, то интерференционные кольца будут стягиваться к центру. При увеличении расстояния на картина принимает прежний вид, так как место каждого кольца будет занято кольцом следующего порядка. С помощью колец Ньютона, как и в опыте Юнга, можно сравнительно простыми средствами приближенно определить длину волны света.

Полосы равной толщины можно наблюдать и с помощью интерферометра Майкельсона, если одно из зеркал з1 или з2 (рис. 8.9) отклонить на небольшой угол.

Итак, полосы равного наклона получаются при освещении пластинки постоянной толщины рассеянным светом, в котором содержатся лучи разных направлений. Полосы равной толщины наблюдаются при освещении пластинки переменной толщины (клина) параллельным пучком света. Полосы равной толщины локализованы вблизи пластинки.

Многолучевая интерференция:

При наложении двух когерентных световых пучков образуются интерференционные полосы, в которых распределение интенсивности описывается функцией I~cos2(kΔ/2) (Δ — разность хода пучков). Максимумы и минимумы интенсивности, т.е. светлые и темные полосы, в двух лучевой интерференционной картине имеют одинаковую ширину. При наложении большого числа пучков распределение интенсивности в интерференционной картине существенно иное. Изменение характера интерференционных полос при увеличении числа n пучков качественно можно предсказать на основе закона сохранения энергии. Амплитуда световых колебаний в максимумах интенсивности, где сложение колебаний происходит в одинаковой фазе, в n раз больше, а интенсивность в n2 раз больше, чем от одного пучка (при условии, что когерентные пучки имеют одинаковую или почти одинаковую интенсивность). Но полная энергия, приходящаяся на одну интерференционную полосу, лишь в n раз больше, чем в одном пучке. Увеличение интенсивности в максимумах в n2 раз возможно только в случае существенного перераспределения потока энергии в пространстве: при прежнем расстоянии между светлыми полосами их ширина должна быть примерно в n раз меньше этого расстояния. Благодаря образованию узких максимумов, т.е. резких светлых полос, разделенных широкими темными промежутками, многолучевая интерференция получила важное практическое применение. Большое число когерентных световых пучков может возникнуть в результате дифракция при прохождении плоской волны через экран с одинаковыми регулярно расположенными отверстиями (метод деления волнового фронта). Распределение интенсивности в такой многолучевой интерференционной картине будет рассмотрено на примере дифракционной решетки. Здесь мы изучим интерференцию при многократных отражениях света от двух параллельных поверхностей (метод деления амплитуды). На этом принципе действует интерферометр Фабри-Перо, широко используемый в спектроскопии высокого разрешения и в метрологии.