
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные функции и собственные значения операторовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Основные свойства собственных функций. Значения, которые может принимать данная физическая величина Если при действии оператора на некоторую функцию получается та же самая функция, умноженная на число, то есть если
то такую функцию называют собственной функцией оператора Квантовомеханические операторы имеют не одну, а множество собственных функций и соответствующих им собственных значений. При этом совокупность собственных значений называют спектром оператора. Спектр оператора
Спектр собственных значений оператора может быть и непрерывным, когда в (3.43) оказываются возможными все значения В ряде случаев одному собственному значению Из (3.43) следует, что собственные функции, вообще говоря, определены с точностью до некоторой постоянной, значение которой обычно выбирают из условия нормировки собственных функций. Докажем, что собственные числа операторов физических величин в квантовой механике всегда являются действительными числами, и это свойство обусловлено самосопряженностью операторов. Действительно, пусть
Выполнив здесь операцию комплексного сопряжения, получим
Если в соотношении (3.42), которое для самосопряженного оператора выполняется тождественно, положить
которое с учетом (3.45) и (3.46) преобразуется к виду
Отсюда следует, что Докажем важное свойство ортогональности собственных функций квантовомеханических операторов. Если
Условие (3.42) самосопряженности оператора
Отсюда с учетом (3.49) получаем
Так как для самосопряженного оператора
Если
Если волновые функции
где символ Кронекера В математической теории линейных самосопряженных операторов доказывается, что система собственных функций квантовомеханических операторов является полной системой функций. Это означает, что всякая волновая функция
Коэффициенты этого разложения (в общем случае комплексные) можно определить, воспользовавшись ортогональностью собственных функций. Действительно, умножим ряд (3.55) на
Отсюда, меняя обозначение
Если оператор
и непрерывное множество коэффициентов
5. Уравнение Шредингера. Стационарное уравнение Шредингера. Отказавшись от описания движения частицы с помощью траекторий, получаемых из законов динамики, и определив вместо этого волновую функцию, необходимо ввести в рассмотрение уравнение, эквивалентное законам Ньютона и дающее рецепт для нахождения
Пусть волновая функция задана в n-мерном конфигурационном пространстве, тогда в каждой точке с координатами
где
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.105.41 (0.01 с.) |

 называют в квантовой механике ее собственными значениями. Нахождение таких значений тесно связано с математической задачей определения собственных функций и соответствующих им собственных значений оператора
называют в квантовой механике ее собственными значениями. Нахождение таких значений тесно связано с математической задачей определения собственных функций и соответствующих им собственных значений оператора  .
. ,
,
 его собственным значением.
его собственным значением. для
для  соответствующих набору собственных функций
соответствующих набору собственных функций  , которые представляют собой регулярные решения уравнения вида
, которые представляют собой регулярные решения уравнения вида
 , либо состоящим из отдельных полос, таких что возможные значения
, либо состоящим из отдельных полос, таких что возможные значения  лежат в ряде интервалов.
лежат в ряде интервалов. оператора
оператора  . Такие случаи называются вырожденными, а число
. Такие случаи называются вырожденными, а число  таких функций называется кратностью вырождения.
таких функций называется кратностью вырождения. - его собственная функция, соответствующая собственному значению
- его собственная функция, соответствующая собственному значению 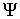 является решением уравнения
является решением уравнения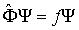 .
.
 .
.
 , то в результате получим интегральное соотношение
, то в результате получим интегральное соотношение ,
,
 .
.
 , т.е собственные значения самосопряженных операторов всегда являются действительными величинами.
, т.е собственные значения самосопряженных операторов всегда являются действительными величинами. и
и  - две собственные функции самосопряженного оператора
- две собственные функции самосопряженного оператора  и
и 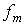 , то они являются решениями следующих уравнений
, то они являются решениями следующих уравнений .
.
 и
и 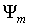 принимает вид
принимает вид .
.
 .
.
 , то (3.51) преобразуется к виду
, то (3.51) преобразуется к виду .
.
 , то
, то  , и из (3.52) получаем условие ортогональности собственных функций, соответствующих различным собственным значениям,
, и из (3.52) получаем условие ортогональности собственных функций, соответствующих различным собственным значениям, .
.
 считать нормированными на единицу, то условие ортогональности (3.53) собственных функций может быть записано как условие ортонормированности
считать нормированными на единицу, то условие ортогональности (3.53) собственных функций может быть записано как условие ортонормированности ,
,
 , и
, и  .
. .
.
 и проинтегрируем по всему пространству. Тогда, изменив порядок суммирования и интегрирования, получим
и проинтегрируем по всему пространству. Тогда, изменив порядок суммирования и интегрирования, получим .
.
 на
на  , получаем формулу для определения коэффициентов
, получаем формулу для определения коэффициентов  в разложении (3.55):
в разложении (3.55): .
.
 , то в разложении любой волновой функции по собственным функциям суммирование переходит в интегрирование. Поэтому
, то в разложении любой волновой функции по собственным функциям суммирование переходит в интегрирование. Поэтому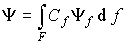 ,
,
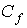 определяется по формуле
определяется по формуле .
.
 в частных физических задачах. Таким уравнением является уравнение Шрёдингера.
в частных физических задачах. Таким уравнением является уравнение Шрёдингера. , в определенный момент времени t она будет иметь вид
, в определенный момент времени t она будет иметь вид  . В таком случае уравнение Шрёдингера запишется в виде:
. В таком случае уравнение Шрёдингера запишется в виде:
 ,
, 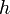 — постоянная Планка;
— постоянная Планка;  — масса частицы,
— масса частицы,  — внешняя по отношению к частице потенциальная энергия в точке
— внешняя по отношению к частице потенциальная энергия в точке  ,
,  — оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла и в n-мерной системе координат имеет вид:
— оператор Лапласа (или лапласиан), эквивалентен квадрату оператора набла и в n-мерной системе координат имеет вид:



