
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерференция в тонких пленках. Полосы равного наклона и равной толщины. Кольца Ньютона.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
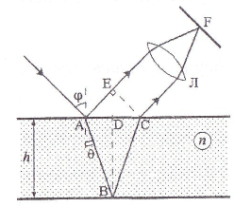
Интерференция в тонких пленках. При распространении световой волны в среде уменьшается скорость распространения волны и соответственно ее длина, т.к. частота не изменяется. При расчете изменения фаз волны в среде в качестве длины пути удобнее брать оптическую длину пути, равную геометрической длине, умноженной на показатель преломления: ∆ = n∆ Полосы равного наклона. Рассмотрим случай, когда плоская монохроматическая волна падает под углом φ на поверхность плоскопараллельной пластинки с относительным показателем преломления п и толщиной h. Интерференция возникает между двумя волнами, отраженными от верхней и нижней поверхностями пластины. Так как эти пучки параллельны между собой, то интерференция наблюдается (локализована) или на бесконечности, или в фокальной плоскости F линзы Л.
Если на пластинку падают непараллельные пучки света, то и интерферирующие пучки будут иметь все всевозможные направления распространения. При заданных толщине пластины и показателе преломления каждому углу падения волны соответствует своя интерференционная полоса. Поэтому такие полосы и называют полосами равного наклона. При аксиально симметричном распределении падающих пучков линии равного наклона являются окружностями. Даже если источник света протяженный, и различные его точки излучают некогерентно, интерференционные картины не зависят от фазы волны в точке расщепления пучков на поверхности пластины (точка А на рис) и от положения этой точки, а зависят лишь от угла падения. Поэтому конечность размеров источника не смазывает картину полос равного наклона и не является ограничивающим интерференцию фактором. Полосы равной толщины. Теперь рассмотрим интерференцию света на пластинке с переменной толщиной (клине) (рис.2). В световом потоке, исходящем из источника S монохроматического света всегда присутствует волна 2, интерферирующая в точке С с волной 1, прошедшей по пути SАВС. Однако в этом случае интерференционная картина локализована на верхней поверхности клина. Интерференционную картину можно также наблюдать и с помощью линзы на экране. В этом случае поверхность проецируется на экран наблюдения. Линии одинаковой интенсивности совпадают с линиями постоянной толщины пластины, поэтому соответствующие интерференционные полосы называются полосами равной толщины. Кольца Ньютона.
Примером интерференционной схемы, в которой наблюдаются полосы равной толщины, является воздушная прослойка, образованная между плоской поверхностью стекла и положенной на нее плосковыпуклой линзой (или наоборот) (рис.3). В этом случае линии равной толщины - окружности, поэтому интерференционная картина имеет вид концентрических колец. Потеря полволны происходит на нижней поверхности воздушного клина. Пусть h - толщина воздушного клина в точке минимума картины (темное кольцо), R - радиус кривизны линзы. Многолучевая интерференция. Интерферометр Фабри-Перо. Многолучевая интерференция. Исследуем сначала интерференцию многих световых волн при прохождении плоской монохроматической волны через плоскопараллельную диэлектрическую пластинку толщиной h и показателем преломления n. Обозначим
где Á и Â – энергетические коэффициенты пропускания и отражения соответственно. Будем считать углы падения j и преломления q достаточно малыми, что можно считать коэффициенты отражения и пропускания независящими от этих углов. Разность хода D между соседними интерферирующими волнами на выходе пластины равна
а разность фаз равна Запаздывание последующей волны относительно предыдущей за счет прохождения волны в пластинке учтем множителем е- id. Суммарная амплитуда E 2 прошедшей волны определяется суперпозицией всех прошедших пластинку волн:
Интенсивность света определяется следующим образом: т.е. при ® 1 Þ V ® 1.
Сканирующий интерферометр Фабри–Перо. Формула Эйри объясняет принцип действия широко используемого в оптике и лазерной технике спектрального прибора – сканирующего интерферометра Фабри–Перо. Это своеобразный аналог измерителей частотных характеристик электрических сигналов радиодиапазона, основанных на принципе сканирования резонансной частоты колебательной системы – колебательного контура, коаксиального, полоскового или объемного резонатора. Заметим, что разность фаз линейно зависит от расстояния между пластинами. Если зафиксировать угол j, то это соответствует помещению некоторого фотоприемника в любую точку экрана (рис.6.8)
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 989; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.198.113 (0.007 с.) |

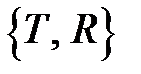 – амплитудные коэффициенты пропускания и отражения при входе волны внутрь пластины,
– амплитудные коэффициенты пропускания и отражения при входе волны внутрь пластины,  – амплитудные коэффициенты пропускания и отражения на выходе волны из пластины наружу.
– амплитудные коэффициенты пропускания и отражения на выходе волны из пластины наружу. При этом справедливы соотношения:
При этом справедливы соотношения: (6.30)
(6.30) , (6.31)
, (6.31) (6.32)
(6.32) .(6.33)
.(6.33) или
или  (6.34)
(6.34) При минимуме прошедшей проинтерферировавшей волны наблюдается максимальное отражение света от интерферометра тоже за счет интерференционного сложения волн на зеркалах.
При минимуме прошедшей проинтерферировавшей волны наблюдается максимальное отражение света от интерферометра тоже за счет интерференционного сложения волн на зеркалах. , где видна интерференционная картина. Оптимальное место для этого – центр картины (точка А), т.к. частотная дисперсия
, где видна интерференционная картина. Оптимальное место для этого – центр картины (точка А), т.к. частотная дисперсия  в этой точке максимальна. Поэтому конечность размеров фотоприемника минимально ухудшает разрешение ИФП как раз при таком местоположении. Теперь допустим, что одна из пластин ИФП параллельно перемещается вдоль оптической оси системы с постоянной скоростью v, т.е. h=h0+ v t. Тогда пропускание ИФП становится зависимым от времени, повторяя зависимость функции Эйри. Если на ИФП падает монохроматическая волна, то на осциллографе, развертка которого движется синхронно с пластиной, сигнал от ИФП опишет его аппаратную функцию в соответствии с (6.34). При сложном спектре электрический сигнал опишет исследуемый спектр. На практике перемещение пластин осуществляется или изменением давления газа между пластинами ИФП, или креплением одной из пластин на пьезокерамику. Второй способ предпочтительней, т.к. позволяет осуществить сканирование величины h(t) электрическим сигналом.
в этой точке максимальна. Поэтому конечность размеров фотоприемника минимально ухудшает разрешение ИФП как раз при таком местоположении. Теперь допустим, что одна из пластин ИФП параллельно перемещается вдоль оптической оси системы с постоянной скоростью v, т.е. h=h0+ v t. Тогда пропускание ИФП становится зависимым от времени, повторяя зависимость функции Эйри. Если на ИФП падает монохроматическая волна, то на осциллографе, развертка которого движется синхронно с пластиной, сигнал от ИФП опишет его аппаратную функцию в соответствии с (6.34). При сложном спектре электрический сигнал опишет исследуемый спектр. На практике перемещение пластин осуществляется или изменением давления газа между пластинами ИФП, или креплением одной из пластин на пьезокерамику. Второй способ предпочтительней, т.к. позволяет осуществить сканирование величины h(t) электрическим сигналом.


