
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отражение и преломление света на границе двух диэлектриков.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
. Граничные условия для векторов поля световой волны на границе между двумя диэлектриками при отсутствии свободных зарядов и токов проводимости имеют вид:
где t, n – индексы тангенциальной (касательной к границе раздела) и нормальной компоненты вектора соответственно. Пусть на плоскую границу двух диэлектриков с абсолютными (не относительными!) проницаемостями (e1; m1) и (e2; m2) падает под некоторым углом плоская световая волна. Тогда для напряженностей электрического поля в падающей, отраженной и преломленной волнах соответственно имеем:
где Для электрического поля граничные условия принимают вид:
Отметим, что начало отсчета вектора r (точка 0’) совершенно произвольно. Если 0’ лежит не на поверхности раздела, то
Равенство будет соблюдаться для произвольных значений r и t только при
Плоскость, в которой лежат волновой вектор k 0и нормаль к поверхности раздела n в точке падения луча, называется плоскостью падения. Из рис. видно, что
Тогда
Введем обозначение При
12. Формулы Френеля для s- и p- поляризаций. Отражение и преломление s- поляризованной ЭМВ. (Рис.4.7)
Как направлены векторы E 1 и E 2 заранее не известно. Направим условно их так, как показано на рис.4.7. Если знак получится отрицательный, значит, векторы направлены в противоположную сторону. Граничные условия для s –поляризации (индексы s опустим):
Для диэлектриков в оптическом диапазоне обычно
Графики зависимостей
При отражении света от диэлектрика с При отражении света от диэлектрика с Отражение и преломление p– поляризованной ЭМВ. (Рис.4.9)
Граничные условия для p –поляризации принимают вид:
Для действительных углов преломления получаем обобщенные формулы Френеля для p–поляризации:
или для диэлектриков с m1 = m2:
Графики зависимостей
13. Энергетические и фазовые соотношения при преломлении и отражении света на границе раздела двух сред. ЯвлениеБрюстера. Явление Брюстера. Из формулы (4.67) и из графика рис.4.10 видно, что для p –поляризованной волны при некотором угле падения Заметим, что явление Брюстера наблюдается тогда, когда направления преломленной и отраженной волны ортогональны. С физической точки зрения это можно объяснить следующим образом. Если связывать наличие отраженной волны с вынужденными колебаниями электронов во второй среде, то в направлении, перпендикулярном преломленной волне, не должна распространяться энергия, т.к. образующийся при этом диполь не излучает в направлении собственных колебаний. При Энергетические соотношения при преломлении и отражении. Энергетическим коэффициентом отражения Энергетический коэффициент пропускания
Т.к. то для имеем:
или с учетом (4.54), (4.55), (4.65), (4.66):
При q0 = 0 для m1 = m2
Прямой проверкой можно показать, что
Это выражает закон сохранения энергии при отражении и преломлении света на границе раздела двух сред. Графики для
Пусть все три волны записаны в виде Далее введем в плоскости падения вдоль границы сред координату x. Из поперечности волн и паралельности векторов
Полное внутреннее отражение света. Примеры его проявления и использования. Явление полного внутреннего отражения. При падении света на границу двух диэлектриков, для которых
Когда угол падения
Но формулы Френеля останутся справедливыми и в этом случае, если закон преломления рассматривать просто как определение входящих в них величин sinq2 и cosq2. Справедливость понимаемых таким образом формул Френеля следует из того, что они обеспечивают выполнение граничных условий и в этом случае. Формулы Френеля для отраженной волны ((4.56) и (4.67) с учетом (4.86)) имеют вид:
Видно, что энергетические коэффициенты
движутся вдоль поверхности раздела и затем возвращаются в первую среду. Места входа энергии во вторую среду и ее возвращения в первую смещены друг относительно друга. Амплитуды p– и s– компонент отраженной волны не изменяются по абсолютному значению, но испытывают различные фазовые сдвиги. Если представить, что
Примеры: 1. Призма–крыша, световоды, миражи, ромб (параллелепипед) Френеля (φ=54,37)
15. Распространение света в проводящих средах. Комплексный показатель преломления. Отражение света от поверхности проводника. Глубина проникновения. Закон Бугера. Распространение света в проводящих средах. При рассмотрении вопроса применения электромагнитной теории Максвелла к данному случаю, задача сводится к учету проводимости металла, т.е. формально к введению в уравнения Максвелла членов, зависящих от коэффициента электропроводности s. Отражение света от поверхности металла, как и его распространение в нем, может быть рассмотрено на основе материальных уравнений, в которых диэлектрическая проницаемость e(w) комплексна. Соответственно показатель преломления n – тоже комплексный: В сильно поглощающих средах и металлах мнимая часть преобладает над вещественной. Частичное проникновение света в металл создает токи проводимости. С ними связано выделение джоулевой теплоты, т.е. поглощение света – необратимое превращение электромагнитной энергии в энергию хаотического теплового движения. Чем выше проводимость металла, тем меньшая доля падающего света проникает в металл и поглощается там. В идеальном проводнике, которому формально соответствует
Пусть из вакуума на металл падает плоская монохроматическая волна с волновым вектором
Видно, что составляющая вектора k 2, направленная вдоль границы вещественна. Поэтому мнимая часть вектора k 2 перпендикулярна поверхности металла. Это значит, что плоскости равных амплитуд прошедшей волны параллельны границе раздела. Вектор Формулы Френеля остаются в силе, если в них рассматривать cosq2 как комплексную величину: Знак корня нужно взять так, чтобы неоднородная волна затухала вглубь металла. Тогда коэффициенты отражения тоже комплексны: При нормальном падении:
При достаточно высоких частотах роль “силы трения” в уравнениях колебаний электрона становится несущественной. Случай g = 0 формально соответствует “идеальному” металлу сs®¥. При В этом случае из (4.102) следует  = 1, т.е. отражение от поверхности идеального проводника полное. Закон Бугера. Для затухающей волны, распространяющейся вдоль оси Z, интенсивность излучения: Отсюда получаем зависимость:
|
|||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.106.95 (0.009 с.) |



 – волновые числа, причем
– волновые числа, причем  – скорости света в 1-й и 2-й средах.
– скорости света в 1-й и 2-й средах.
 .
.
 . Отсюда следует, что
. Отсюда следует, что  . (Частота ЭМВ при отражении и преломлении не меняется.)
. (Частота ЭМВ при отражении и преломлении не меняется.)

 или:
или:  . Вспомним, что
. Вспомним, что  – показатели преломления.
– показатели преломления. .
.  .(Закон Снеллиуса)
.(Закон Снеллиуса) – относительный показатель преломления. Тогда закон Снеллиуса примет вид:
– относительный показатель преломления. Тогда закон Снеллиуса примет вид:  .
. (падение из менее оптически плотной в более оптически плотную среду)
(падение из менее оптически плотной в более оптически плотную среду)  (рис.4.4). При
(рис.4.4). При 
 (рис.4.5).
(рис.4.5).


 (4.42) – (4.43)Обозначим:
(4.42) – (4.43)Обозначим:  – амплитудный коэффициент отражения;(4.51)
– амплитудный коэффициент отражения;(4.51)  – амплитудный коэффициент пропускания. (4.52)При
– амплитудный коэффициент пропускания. (4.52)При  система
система  имеет действительное решение для всех углов q0. Если
имеет действительное решение для всех углов q0. Если  она имеет действительное решение лишь для углов
она имеет действительное решение лишь для углов  (подробнее этот случай рассмотрим позднее). Тогда имеем:
(подробнее этот случай рассмотрим позднее). Тогда имеем: (4.54) – (4.55)(Обобщенные формулы Френеля для s – поляризации)
(4.54) – (4.55)(Обобщенные формулы Френеля для s – поляризации) . Тогда из (4.54) и (4.55) получим общепринятые формулы Френеля для s – поляризации:
. Тогда из (4.54) и (4.55) получим общепринятые формулы Френеля для s – поляризации: (4.56) – (4.57)
(4.56) – (4.57) и
и  для
для  приведены на рис.4.8.
приведены на рис.4.8.
 скачка фазы на p не происходит ни для отраженной, ни для преломленной волны (для углов
скачка фазы на p не происходит ни для отраженной, ни для преломленной волны (для углов  рассмотрение – ниже).
рассмотрение – ниже).
 (4.61) – (4.62)
(4.61) – (4.62)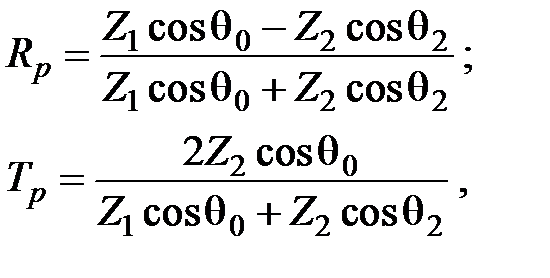 (4.65) – (4.66)
(4.65) – (4.66) (4.67) – (4.68)
(4.67) – (4.68)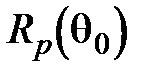 и
и  для
для 
 , называемом углом Брюстера, отраженная волна отсутствует, т.е.
, называемом углом Брюстера, отраженная волна отсутствует, т.е.  . Это явление называется явлением Брюстера (1815 г.). Для угла Брюстера справедливы следующие соотношения:
. Это явление называется явлением Брюстера (1815 г.). Для угла Брюстера справедливы следующие соотношения:  (4.69) При переходе через угол Брюстера фаза колебаний отраженной волны скачком меняется на p.
(4.69) При переходе через угол Брюстера фаза колебаний отраженной волны скачком меняется на p. называется абсолютное значение отношения нормальных компонент векторов Пойнтинга в отраженной и падающих волнах:
называется абсолютное значение отношения нормальных компонент векторов Пойнтинга в отраженной и падающих волнах:  (4.72)
(4.72) вводится аналогичным образом для преломленной волны:
вводится аналогичным образом для преломленной волны: . (4.73)
. (4.73) ,(4.74)
,(4.74)  (4.75)
(4.75) (4.76)
(4.76) (4.77)
(4.77) ; (4.78)
; (4.78) ; (4.79)
; (4.79) ; (4.80)
; (4.80) . (4.81)
. (4.81) ;(4.82)
;(4.82)  . (4.83)
. (4.83) .(4.84)
.(4.84) изображены на рис.4.11.
изображены на рис.4.11. 

 Очевидно, для линейной среды зависимость H (r,t) или B( r,t) будет иметь точно такой же вид. Воспользуемся для случая (а) граничным условием
Очевидно, для линейной среды зависимость H (r,t) или B( r,t) будет иметь точно такой же вид. Воспользуемся для случая (а) граничным условием 
 следует, что все три волновых вектора
следует, что все три волновых вектора  лежат в одной плоскости — падения. Вдоль оси Ox произведения kr в формулах типа (2.6.1) вырождаются в
лежат в одной плоскости — падения. Вдоль оси Ox произведения kr в формулах типа (2.6.1) вырождаются в  . Т.о., граничное условие при равных частотах сводится к следующему:
. Т.о., граничное условие при равных частотах сводится к следующему: 
 , из закона Снеллиуса следует, что существует предельный (или критический) угол qп падения, при котором угол преломления
, из закона Снеллиуса следует, что существует предельный (или критический) угол qп падения, при котором угол преломления  . Тогда
. Тогда  .При
.При  угол преломления q2 имеет обычную геометрическую интерпретацию, и коэффициенты R и T являются вещественными.
угол преломления q2 имеет обычную геометрическую интерпретацию, и коэффициенты R и T являются вещественными.
 , не существует вещественного угла преломления q2, т.к. закон Снеллиуса дает для sinq2 значение больше единицы, а для cosq2 – чисто мнимое значение:
, не существует вещественного угла преломления q2, т.к. закон Снеллиуса дает для sinq2 значение больше единицы, а для cosq2 – чисто мнимое значение:
 ;
;  .
. при углах падения больше критического. Поэтому это явление называется полным внутренним отражением (ПВО). При этом волна и соответствующая доля энергии проникают через границу раздела во вторую среду на некоторую глубину d (глубину проникновения) (амплитуда поля на глубине d падает в е раз)
при углах падения больше критического. Поэтому это явление называется полным внутренним отражением (ПВО). При этом волна и соответствующая доля энергии проникают через границу раздела во вторую среду на некоторую глубину d (глубину проникновения) (амплитуда поля на глубине d падает в е раз) ,
, , то
, то 
 Обозначим
Обозначим  Тогда
Тогда  .
.
 .(4.96)
.(4.96) , потери на джоулеву теплоту вообще отсутствуют, так что падающий свет полностью отражается.
, потери на джоулеву теплоту вообще отсутствуют, так что падающий свет полностью отражается. (рис.4.14);
(рис.4.14);
 – волновой вектор отраженной волны. Во второй среде волна неоднородна и
– волновой вектор отраженной волны. Во второй среде волна неоднородна и  . (4.97)Тогда, как и при выводе формул Френеля:
. (4.97)Тогда, как и при выводе формул Френеля:  .(4.98)
.(4.98) перпендикулярен плоскостям постоянных фаз и характеризует направление прошедшей волны. Угол y называется вещественным углом преломления. Отношение
перпендикулярен плоскостям постоянных фаз и характеризует направление прошедшей волны. Угол y называется вещественным углом преломления. Отношение  зависит от угла падения (в отличие от диэлектриков).
зависит от угла падения (в отличие от диэлектриков). .(4.99)
.(4.99) (4.100)В общем случае
(4.100)В общем случае  . При линейной поляризации падающего света с произвольным азимутом в отраженной волне появляется сдвиг фаз, приводящий к эллиптической поляризации отраженного света. Отраженный свет остается линейно поляризованным, если: 1) падающий свет s– или p– поляризован; 2)
. При линейной поляризации падающего света с произвольным азимутом в отраженной волне появляется сдвиг фаз, приводящий к эллиптической поляризации отраженного света. Отраженный свет остается линейно поляризованным, если: 1) падающий свет s– или p– поляризован; 2)  ;3)
;3) 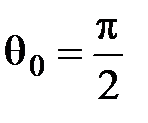 .
. ; (4.101)
; (4.101)  .(4.102)У металлов c2 значительно больше другого слагаемого. Поэтому
.(4.102)У металлов c2 значительно больше другого слагаемого. Поэтому  .Волновой вектор прошедшей в металл волны при нормальном падении имеет только z – составляющую:
.Волновой вектор прошедшей в металл волны при нормальном падении имеет только z – составляющую: ;(4.103)
;(4.103) — глубина проникновения. (4.104)
— глубина проникновения. (4.104) , а
, а  .(4.105)
.(4.105) . (4.106)
. (4.106) ,(4.107)называемая законом Бугера, где a – линейный показатель поглощения. Другой вид закона Бугера (см. (4.104)):
,(4.107)называемая законом Бугера, где a – линейный показатель поглощения. Другой вид закона Бугера (см. (4.104)): ,(4.108)где l0 – длина волны света в вакууме.
,(4.108)где l0 – длина волны света в вакууме.


