
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение отражения и преломления светаСодержание книги
Поиск на нашем сайте
ИЗУЧЕНИЕ ДИФРАКЦИИ СВЕТА
Дифракция – это явление огибания волнами препятствий, захождение волн в область геометрической тени. При дифракции волн за препятствием образуются области усиления и ослабления колебаний, что может быть объяснено как результат интерференции. Задачи дифракции решают с помощью принципа Гюйгенса – Френеля. Каждая точка однородного изотропного пространства, до которой дошла волна, является источником вторичных полусферических волн. Амплитуда и фаза колебания в некоторой точке наблюдения перед фронтом распространения волны является результатом интерференции вторичных волн, с учетом их фаз и амплитуд. То есть дифракция – это явление интерференции вторичных волн. В приближенном решении задач дифракции используют метод зон Френеля. Суть метода состоит в том, что бесконечное число вторичных точечных источников объединяют в зоны таким образом, чтобы разность хода вторичных волн от двух соседних зон Френеля до точки наблюдения была равна половине длины волны. В этом случае волны от соседних зон в точке наблюдения оказываются в противофазе и могут полностью или частично компенсировать друг друга. Рассмотрим дифракцию параллельного пучка света, падающего нормально, на длинную узкую щель. Каждая точка щели, согласно принципу Гюйгенса – Френеля, становится источником вторичных волн, распространяющихся в пределах от – 90о до + 90о относительно направления падающей волны. Вторичные волны когерентны. Соберем с помощью линзы вторичные волны, параллельные некоторому направлению, на экране в фокальной плоскости линзы F. В центре экрана соберутся вторичные волны, излученные по нормали к щели. Они усиливают друг друга, поскольку их оптический путь одинаков, а линза обладает свойством не изменять оптический путь. Для центрального максимума щель является одной зоной Френеля (рис. 1).
Если число зон будет нечетным, то свет от одной из зон окажется не скомпенсированным и в точке наблюдения будет максимум освещенности. Дифракционная картина от одной щели очень слаба. Для ее усиления применяют дифракционные решетки из большого числа щелей. Дифракционная решетка – это оптическое устройство, представляющее собой систему большого числа одинаковых, параллельных щелей, расположенных на одинаковом расстоянии друг от друга. Параметром решетки является период решетки – расстояние между соседними щелями, равное сумме ширины прозрачного и непрозрачного промежутков: d = а + b. Пусть на дифракционную решетку падает нормально параллельный пучок света (рис. 2). Каждая щель становится источником вторичных волн, излучаемых в направлении от –90о до + 90о. Соберем с помощью линзы параллельные пучки света от каждой щели в фокальной плоскости линзы на экране. Они будут усиливать друг друга при интерференции, если оптическая разность хода от соседних щелей будет кратна целому числу длин волн, D L = к l. Из рис. 2 видно, что оптическая разность хода равна D L = d sin a. Тогда условие образования главных максимумов примет вид d sin a = кl, (1)
где к = 0, 1, 2, 3,... – целое число, являющееся порядком максимума.
Дифракционная решетка является спектральным прибором. Если решетка освещается белым светом, то главные максимумы, кроме центрального, разлагаются в спектр. Согласно формуле (2), чем меньше длина волны, тем ближе к центру расположена спектральная линия этого цвета. Поэтому спектр начинается с фиолетового и заканчивается красным цветом. В лабораторной установке свет от источников проходит через узкую щель и затем, дифрагируя на решетке, попадает в глаз наблюдателя. Хрусталик глаза является линзой, создающей изображение на сетчатке глаза. Изображение спектров воспринимается как бы расположенным на линейке (рис. 4).
ИЗУЧЕНИЕ ФОТОЭФФЕКТА Внешний фотоэффект – это явление испускания электронов телами под действием света. Экспериментальное исследование фотоэффекта впервые провел А. Г. Столетов. Вакуумный фотоэлемент (стеклянный баллон с электродами) включался в цепь источника постоянного тока. Катод из исследуемого металла освещался монохроматическим светом. Исследовалась зависимость силы фототока от напряжения (вольтамперная характеристика), от частоты монохроматического излучения, от освещенности.
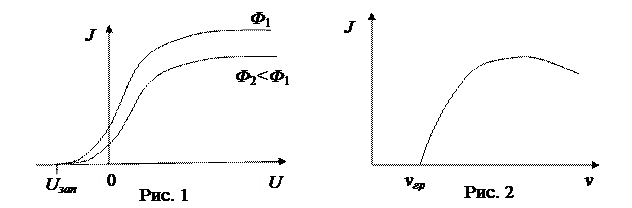
Рассмотрим вольтамперную характеристику (рис. 1). При отсутствии напряжения сила фототока не равна нулю, так как электроны, вылетая из катода при его освещении, образуют электронное облако, из которого они из-за теплового движения могут попадать на анод и перемещаться по внешней цепи обратно на катод. С ростом прямого напряжения все большая часть электронов под действием электрического поля попадает на анод и сила фототока быстро возрастает. Когда все испускаемые катодом электроны попадают на анод, сила фототока достигает насыщения. Сила тока насыщения равна заряду электронов, испускаемых катодом и попадающих на анод в единицу времени, J = e n. При смене полярности с ростом напряжения сила фототока падает, так как запирающее электрическое поле препятствует попаданию на анод сначала медленных электронов, а затем самых быстрых. Напряжение, при котором сила фототока падает до нуля, называется запирающим. Его величина определяется из закона сохранения энергии: кинетическая энергия самых быстрых электронов расходуется на совершение работы против сил поля
При изучении зависимости силы фототока от частоты монохроматического света (спектральная характеристика фотоэлемента) обнаружено, что фотоэффект возможен только в диапазоне частот выше так называемой красной границы (рис. 2). На основании экспериментов Столетов установил законы фотоэффекта. 1. Сила фототока насыщения при освещении катода монохроматическим светом прямо пропорциональна световому потоку. 2. Максимальная кинетическая энергия фотоэлектронов не зависит от освещенности, а линейно зависит от частоты. 3. Для каждого металла существует так называемая красная граница фотоэффекта, то есть граничная частота, ниже которой фотоэффект не происходит. Волновая теория света не смогла объяснить законы фотоэффекта. По этой теории электроны в металле раскачиваются в электрическом поле световой волны любой частоты и, набрав за некоторое время достаточно энергии, вылетают из металла. На самом деле фотоэффект практически безинерционен и существует граничная частота. По волновой теории кинетическая энергия должна быть пропорциональна амплитуде напряженности поля, то есть освещенности. На самом деле энергия фотоэлектронов от освещенности не зависит. Закономерности фотоэффекта объяснила квантовая теория света. По этой теории свет – это поток фотонов, излученных атомами и молекулами вещества. Энергия фотона определяется по формуле Планка, e = h n, где h = 6,63 10 –34 Дж∙с – постоянная Планка, n – частота излучения. При фотоэффекте фотоны, попадая в металл, взаимодействуют с электронами. Это процесс неупругого взаимодействия, после которого фотон, отдав энергию электрону, перестает существовать. Если электрон, получив избыточную энергию, движется к поверхности, то он имеет шанс вылететь за пределы металла. Закон сохранения энергии для фотоэффекта, называемый уравнением Эйнштейна, имеет вид
Энергия, полученная электроном от фотона, расходуется им на совершение работы выхода из металла А и на приобретение кинетической энергии. Работа выхода электрона обусловлена преодолением двойного тормозящего электрического слоя, образованного свободными электронами над поверхностью металла, и взаимодействием с зарядившимся положительно металлом. Не все электроны вылетают с максимальной скоростью, согласно уравнению (2). Некоторые теряют часть энергии, взаимодействуя с атомами внутри металла, и вылетают с меньшей скоростью. Уравнение Эйнштейна объясняет закономерности фотоэффекта. Во-первых, сила фототока насыщения пропорциональна световому потоку, так как пропорционально растет число фотонов. Во-вторых, максимальная кинетическая энергия фотоэлектронов, согласно уравнению Эйнштейна, зависит только от частоты по линейному закону. В-третьих, с уменьшением частоты света, при некоторой так называемой граничной частоте, даже самому быстрому электрону хватает энергии только на то, чтобы выйти за пределы металла. Если частота будет меньше граничной, то энергия электрона будет недостаточна для совершения работы выхода и фотоэффекта не будет: hnгр = А. (3) Лабораторное изучение явления внешнего фотоэффекта производится с вакуумным фотоэлементом СЦВ (рис. 3). Катод из сурьмяно-цезиевого сплава напылен на часть стенки стеклянного баллона. Анодом является кольцо в центре баллона. Фотоэлемент освещается светом лампы накаливания, проходящим через один из светофильтров. Фотоэлемент подключен к электронному блоку, в котором собрана электрическая цепь с индикаторами силы фототока и напряжения. Полярность устанавливается тумблером «ускоряющее − запирающее» (+ −). Напряжение регулируется ручками «грубо − точно»
на передней панели электронного блока. ИЗУЧЕНИЕ ПОЛЯРИЗАЦИИ СВЕТА
Рассмотрим поляризацию света при отражении от диэлектриков. Пусть естественный свет падает под некоторым углом на гладкую поверхность диэлектрика, на которой он частично отражается и частично преломляется. Разложим световые векторы в падающем луче на два направления, параллельно и перпендикулярно плоскости падения. Отраженный свет состоит из волн, излученных электронами диэлектрика, которые совершают вынужденные колебания под действием электрического поля преломленной волны. Известно, что в направлении колебаний электрон не излучает волн. Рассмотрим отражение компоненты луча света, в которой световые векторы совершают колебания параллельно плоскости падения. Если угол между преломленным лучом света и отраженным будет точно равен 90о, то направление колебаний электронов диэлектрика окажется параллельным направлению отраженного луча. Но в этом направлении электроны не излучают, и, значит, отраженного луча не будет (рис. 2а). Но зато отразится вторая компонента луча света, в которой световые векторы совершают колебания перпендикулярно плоскости падения (рис. 2б). Этот свет будет плоскополяризованным. При падении естественного света под другими углами в отраженном свете будут обе компоненты, и свет будет поляризован частично.
tg b = n. (1)
Это уравнение закона Брюстера: тангенс угла максимальной поляризации света при отражении от диэлектриков равен относительному показателю преломления. Рассмотрим поляризацию света при прохождении через двоякопреломляющие кристаллы. В анизотропных кристаллах, в отличие от изотропных веществ, физические свойства зависят от направления, например диэлектрическая проницаемость и связанная с ней скорость света. Пусть, например, в простейшем одноосном кристалле скорость распространения света наибольшая, если световой вектор электромагнитной волны перпендикулярен оптической оси кристалла. Рассмотрим падение на поверхность кристалла естественного света. Представим его в виде двух пучков. Пусть в первом пучке колебания совершаются в плоскости, в которой лежит оптическая ось кристалла О–О, а в другом – перпендикулярно (рис. 3). По принципу Гюйгенса каждая точка поверхности кристалла является источником вторичных волн. В первом случае волны, распространяющиеся вдоль оси О–О, будут иметь наибольшую скорость, а в других направлениях – меньшую. Огибающая вторичных волн оказывается эллипсоидом, а фронт преломленного пучка, в нарушение закона преломления света, смещается от нормали. Этот луч света называется необыкновенным. Во втором случае световые векторы всех вторичных волн перпендикулярны оптической оси, скорость света во всех направлениях одинакова и наибольшая, и фронты вторичных волн являются полусферами. Этот луч света распространяется в кристалле по законам преломления света, и его называют обыкновенным.
Рассмотримпрохождение света через два поляризатора. Представим луч естественного света в виде двух лучей (рис. 4). В первом колебания светового вектора параллельны плоскости пропускания поляризатора П–П, и этот луч пройдет в идеальном случае без ослабления. Во втором луче световые векторы перпендикулярны плоскости пропускания, и он полностью гасится. Таким образом, вышедший из поляризатора луч является плоско поляризованным, а его интенсивность равна половине интенсивности падающего на поляризатор естественного света: J пол= Jест / 2.
Пусть далее пучок поляризованного света падает на второй поляризатор, который называют анализатором. Через него пройдет только та составляющая, в которой световой вектор параллелен плоскости пропускания: Е ан = Е пол cos a. Интенсивность света пропорциональна квадрату светового вектора. Поэтому
J ан = J пол cos 2 a. (2)
Это закон Малюса: интенсивность поляризованного света после прохождения анализатора пропорциональна квадрату косинуса угла между плоскостью колебаний светового вектора в падающем поляризованном свете и плоскостью пропускания анализатора.
Если на анализатор падает плоско поляризованный свет, то при
 ворачивать вокруг исследуемого луча.
ПОЛУПРОВОДНИКОВ
Полупроводники – это кристаллические тела, которые по электропроводности занимают промежуточное положение между металлическими проводниками и изоляторами. Но принципиальным отличием полупроводников от металлов является быстрое уменьшения сопротивления с ростом температуры, в то время как у металлов оно медленно растет. Также электропроводность полупроводников сильно зависит от примесей. Полупроводники – это, как правило, кристаллы элементов 4-й группы таблицы Менделеева, например германия, кремния. При образовании кристалла между атомами возникает химическая связь четырех валентных электронов. При абсолютном нуле температуры все электроны связаны, и кристалл является изолятором. Но при комнатных температурах некоторые электроны, получив достаточную энергию теплового движения, могут оторваться от атома, стать свободными. Одновременно образуется вакантная, незаполненная связь, которую может занять какой-либо электрон из соседних атомов, оставив после себя вакантную связь, которую может занять следующий электрон. Прыжки большого числа электронов эквивалентны перемещению положительного электрического заряда, так называемой «дырки». В электрическом поле электроны и дырки перемещаются в противоположных направлениях, создавая электрический ток. С ростом температуры число свободных электронов и дырок растет, что приводит к уменьшению сопротивления.
Кристалл является полупроводником, если валентная зона заполнена полностью, а зона проводимости отделена так называемой запрещенной зоной, ширина которой не более 2 электрон-вольт. При нуле абсолютной температуры ни тепловое движение, ни электрическое поле не в состоянии сообщить добавочную энергию электрону для перехода в зону проводимости и кристалл является изолятором. Но при комнатной температуре энергия теплового движения уже достаточна для ионизации атомов. Освободившиеся электроны переходят в зону проводимости и получают право перемещаться по кристаллу. Концентрация свободных электронов определяется распределением Больцмана:
Здесь n 0– концентрация всех валентных электронов, Ε – ширина запрещенной зоны или энергия активации, кТ – мера энергии теплового движения электрона, равная произведению постоянной Больцмана на температуру. Сопротивление кристалла обратно пропорционально концентрации электронов в зоне проводимости и дырок в валентной зоне, поэтому
Здесь R 0 – сопротивление полупроводника, если бы все валентные электроны стали свободными. Коэффициент «2» учитывает энергию активации, приходящуюся на два возникающих вместе заряда – на электрон и дырку.
Если в кристалл 4-валентного полупроводника внести атомы 3-валентной примеси, например индия, бора, то одна связь окажется незаполненной. Образуется дырка. Энергия электрона, занявшего дырку, немного больше, чем у других валентных электронов. Этот уровень энергии, называемый акцепторным, чуть выше потолка валентной зоны. Получив добавочную энергию Еакц,, на акцепторный уровень переходят электроны из валентной зоны, а в валентной зоне остается дырка. Дырки являются основными носителями заряда. Такие кристаллы называются полупроводниками p -типа (рис. 2). Примесная составляющая сопротивления полупроводников определяется формулой
Полная электропроводность кристалла полупроводника складывается из собственной и примесной. При сравнительно низких температурах главную роль играет примесная проводимость, так как энергия активации примеси невелика. Но с ростом температуры рост концентрации электронов, или дырок, при почти полной ионизации сравнительно небольшого числа атомов примеси прекратится. Зато растет число электронов и дырок при ионизации собственных атомов кристалла. Собственная проводимость становится преобладающей при высоких температурах. Если уравнения (2) и (3) прологарифмировать, то получим линейные уравнения для собственной и для примесной проводимости:
Логарифмы обоих видов сопротивлений линейно зависят от обратной температуры (рис. 3). Их угловые коэффициенты соответственно будут равны Исследование температурной зависимости сопротивления полупроводника проводится на установке (рис. 4). Полупроводником является терморезистор, помещенный в электронагреватель. Температура и сопротивление определяются по показаниям индикаторов электронного блока.
Оптика Атомная физика Учебно-методическое пособие к лабораторным занятиям
Второе издание, дополненное
Составитель Шушарин Анатолий Васильевич
Редактор Л. Л. Шигорина Компьютерная верстка О. Г. Пироговой
Подписано в печать 30.03.08. Формат 60 х 84 1/16. Тираж 200 экз. Заказ 11. Цена договорная
Отпечатано в Издательском центре ЧИПС 454111 Челябинск, ул. Цвиллинга, 56
Для заметок ИЗУЧЕНИЕ ОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ СВЕТА Геометрическая оптика – это раздел оптики, изучающий распространение света в прозрачных средах, отражение и преломление лучей света на границе раздела сред. Луч света – это пучок света малого поперечного сечения. В геометрической оптике размеры границ сред считаются намного больше длины волны, так что дифракционными явлениями можно пренебречь. Экспериментально установлены следующие законы геометрической оптики.
2. Закон отражения света. При падении луча света на зеркальную поверхность он отражается. Луч падающий, отражённый и нормаль в точке падения лежат в одной плоскости. Угол падения равен углу отражения α = γ (рис. 1). 3. Закон преломления света. При падении луча света на границу раздела двух прозрачных сред луч света частично отражается, частично переходит во вторую среду и преломляется. Луч падающий, преломлённый и нормаль к поверхности в точке падения лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления для данной пары сред постоянно и равно относительному показателю преломления (рис.1)
Если луч света падает на границу с оптически менее плотной средой, например из стекла в воздух, то преломленный луч отклоняется от нормали на угол, больший угла падения. При падении под некоторым углом, названным предельным углом полного внутреннего отражения αпр, преломлённый луч отклонится на угол β = 90о и будет распространяться по поверхности раздела сред (рис. 2). Если угол падения ещё увеличить, то преломленный луч исчезнет. Останется только отражённый луч, интенсивность которого по закону сохранения энергии равна интенсивности падающего луча. Это явление называется полным внутренним отражением. Предельный угол полного внутреннего отражения, согласно закону преломления при β = 90о, можно определить по формуле
где n 12– относительный показатель преломления первой, оптически более плотной среды, по отношению ко второй. Теоретическим обоснованием законов геометрической оптики является принцип Гюйгенса: точки среды, до которых дошла волна, становятся источниками вторичных волн. В однородной изотропной среде фронт вторичных волн – полусфера. Огибающая поверхность фронтов вторичных волн определяет новое положение фронта волны, а нормаль к фронту – направление распространения луча. В качестве примера выведем закон преломления света. Пусть на границу двух сред падает параллельный пучок света. Как только фронт падающей волны в точке А коснётся границы, от этой точки начнёт распространяться вторичная волна (рис.3). В момент, когда фронт падающей волны дойдёт через время τ = BC/V 1 до точки С, от точки А распространится вторичная волна на расстояние V 2∙ τ, где V 2 – скорость распространения волны во второй среде. Для других источников на границе радиусы фронтов будут меньше. Огибающая фронтов вторичных волн СД будет фронтом преломленной волны. Для треугольников АВС и АСД можно составить отношение синусов угла падения α и угла преломления β:
Если сопоставить уравнение (3) с законом преломления света (1), то не только подтвержден закон преломления, но и установлен физический смысл относительного показателя преломления. Показатель преломления равен отношению скоростей света в этих средах  . Соответственно абсолютный показатель преломления равен отношению света в вакууме к скорости света в среде. . Соответственно абсолютный показатель преломления равен отношению света в вакууме к скорости света в среде.
Экспериментальное исследование законов отражения и преломления света производится на установке (рис.4). Луч света от лазера падает по радиусу на цилиндрическую поверхность стеклянного полуцилиндра и, не преломляясь, попадает в центр нижней грани. В этой точке на границе с воздухом луч частично отражается, частично преломляется. Поворачивая визир, ловят преломленный луч, наблюдая его через щель визира. Углы
2. Интерференция – это явление сложения когерентных волн, при котором возникают области усиления и ослабления колебаний. При интерференции происходит перераспределение энергии из области ослабления в область усиления. При этом на экране будут наблюдаться темные и светлые полосы. Устойчивую интерференционную картину можно наблюдать только при сложении когерентных волн. Это волны, разность фаз которых в точке наблюдения остается постоянной и, кроме того, для поперечных световых волн направления колебаний световых векторов волн должны быть параллельны. Свет от некогерентных источников, например от двух лампочек, не создает устойчивой картины интерференции. Даже если в какой-то точке два цуга волн, излученных разными атомами, усиливают друг друга, то примерно через 10-8 с они сменяются другими, которые могут ослаблять друг друга. В результате на экране интенсивность освещения быстро и хаотично меняется, а глаз в силу инерционности восприятия наблюдает равномерную освещенность. Когерентные волны получают разделением пучка света на два пучка при отражении или преломлении. Затем эти волны, распространяясь каждая по своему пути, снова встречаются и интерферируют. Условием усиления колебаний когерентных волн является совпадение направлений колебаний световых векторов в точке наблюдения. Это будет, если разность фаз колебаний кратна 2 p радиан: D j = 2 кp. Наибольшее ослабление колебаний будет, если направления колебаний световых векторов противоположны, разность фаз кратна нечетному числу p радиан: D j = ( 2 к+ 1 )p. Здесь к – целое число, обычно небольшое для не идеально монохроматического света, к = 0,1,2,3 и т. д. Пусть в некоторой точке пространства встречаются две когерентные волны, уравнения которых имеют вид
Здесь w – циклическая частота, одинаковая для обеих волн. Аргумент косинуса называется фазой колебаний. Разность фаз колебаний двух волн, прошедших разные расстояния l 1 и l 2 в разных средах с различной длиной волны l 1 и l 2 , будет равна: Подставив условие усиления и ослабления волн при интерференции в уравнение разности фаз волн (1), получим, что волны усиливают друг друга, если разность оптических путей кратна четному числу длин полуволн, и ослабляют, если равна нечетному числу длин полуволн.
mах: l 2 n 2 – l 1 n 1 = кl (2), min: l 2 n 2 - l 1 n 1 = ( 2 к + 1 )l/ 2. (3)
Оптический путь зависит также от условий отражения света. Если свет отражается от оптически более плотной среды, с большим показателем преломления, то в отраженной волне фаза изменяется на p радиан. Это соответствует увеличению оптического пути этого луча на половину длины волны, l /2. Рассмотрим частный случай явления интерференции – образование колец Ньютона. Для наблюдения интерференционных колец плосковыпуклую линзу большого радиуса кривизны поверхности, положенную выпуклой стороной на стеклянную пластинку, освещают параллельным пучком света. Когерентные лучи 1 и 2 образуются при отражении света от поверхностей воздушного клина между нижней поверхностью линзы и стеклянной пластинкой (рис. 1).
Если оптическая разность хода удовлетворяет условию минимума, то во всех точках с одинаковой толщиной воздушного зазора будет минимум освещенности, и эти точки образуют темное кольцо. В монохроматическом свете интерференционная картина будет иметь вид темных и светлых колец, в белом – радужных. В центре колец будет темное пятно, так как толщина зазора здесь стремится к нулю, а разность оптических путей D L ® l/ 2, что соответствует условию минимума. Толщину воздушного зазора, например для темных колец, определим, п
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.184.124 (0.018 с.) |

 Для определения интенсивности в стороне от центра разделим поверхность щели на зоны Френеля плоскостями, отстоящими друг от друга на полволны. Зоны Френеля будут иметь вид ряда узких полосок, параллельных кромкам щели. Если число зон окажется четным, то в результате интерференции свет от каждой пары соседних зон гасится и в точке наблюдения на экране будет минимум освещенности. То есть условие минимума будет
Для определения интенсивности в стороне от центра разделим поверхность щели на зоны Френеля плоскостями, отстоящими друг от друга на полволны. Зоны Френеля будут иметь вид ряда узких полосок, параллельных кромкам щели. Если число зон окажется четным, то в результате интерференции свет от каждой пары соседних зон гасится и в точке наблюдения на экране будет минимум освещенности. То есть условие минимума будет , m = 1, 2, 3..
, m = 1, 2, 3.. Принципиальное отличие от дифракции света на щели состоит в том, что главные максимумы при дифракции на решетках оказываются очень узкими и отделены друг от друга большими темными промежутками. Объяснить это можно, применяя метод векторных диаграмм для сложения амплитуд вторичных волн от всех щелей. Амплитуда главного максимума равна Е = Е 1 N, так как вторичные волны приходят в одинаковой фазе (рис. 3 а). Но стоит сместиться по экрану чуть в сторону от центрального максимума, как между вторичными волнами появляется небольшая разность фаз. Если она станет равна 2 p /N, то векторная диаграмма превратится в окружность и результирующий вектор амплитуды обращается в нуль (рис. 3 б). Разности фаз 2 p /N соответствует разность хода D L = l/N, и угол образования первого минимума будет мал: d sin amin =l/N. .
Принципиальное отличие от дифракции света на щели состоит в том, что главные максимумы при дифракции на решетках оказываются очень узкими и отделены друг от друга большими темными промежутками. Объяснить это можно, применяя метод векторных диаграмм для сложения амплитуд вторичных волн от всех щелей. Амплитуда главного максимума равна Е = Е 1 N, так как вторичные волны приходят в одинаковой фазе (рис. 3 а). Но стоит сместиться по экрану чуть в сторону от центрального максимума, как между вторичными волнами появляется небольшая разность фаз. Если она станет равна 2 p /N, то векторная диаграмма превратится в окружность и результирующий вектор амплитуды обращается в нуль (рис. 3 б). Разности фаз 2 p /N соответствует разность хода D L = l/N, и угол образования первого минимума будет мал: d sin amin =l/N. . Угловое положение спектральной линии определяется по расстояние l от щели до линии и от щели до решетки L, по формуле
Угловое положение спектральной линии определяется по расстояние l от щели до линии и от щели до решетки L, по формуле  .
.
 . (1)
. (1) . (2)
. (2)
 Пучок света состоит из огромного числа фотонов, испущенных разными атомами источника света. Вследствие того, что атомы излучают фотоны независимо друг от друга, направления колебаний световых векторов в сечении пучка света расположены хаотично. Такой свет называется естественным. Если каким-либо образом упорядочить направления колебаний световых векторов, например, параллельно друг другу, то такой свет будет плоскополяризованным (рис. 1).
Пучок света состоит из огромного числа фотонов, испущенных разными атомами источника света. Вследствие того, что атомы излучают фотоны независимо друг от друга, направления колебаний световых векторов в сечении пучка света расположены хаотично. Такой свет называется естественным. Если каким-либо образом упорядочить направления колебаний световых векторов, например, параллельно друг другу, то такой свет будет плоскополяризованным (рис. 1).
 . Откуда получим
. Откуда получим

 Деление твердых тел на проводники, полупроводники и изоляторы объясняет зонная теория. В свободных атомах электроны имеют совершенно одинаковый дискретный набор дозволенных уровней энергии. Но при объединении N ≈ 1023 атомов в кристалл электроны взаимодействуют не с одним, а со всеми атомами кристалла. В результате некоторый уровень энергии свободного атома в кристалле «расщепляется» на N уровней с ничтожно малой (10 –23 эВ) разностью энергий. Эти N уровней энергии образуют энергетическую зону. Каждый уровень энергии в зоне, согласно принципу Паули, могут занимать не более двух электронов.
Деление твердых тел на проводники, полупроводники и изоляторы объясняет зонная теория. В свободных атомах электроны имеют совершенно одинаковый дискретный набор дозволенных уровней энергии. Но при объединении N ≈ 1023 атомов в кристалл электроны взаимодействуют не с одним, а со всеми атомами кристалла. В результате некоторый уровень энергии свободного атома в кристалле «расщепляется» на N уровней с ничтожно малой (10 –23 эВ) разностью энергий. Эти N уровней энергии образуют энергетическую зону. Каждый уровень энергии в зоне, согласно принципу Паули, могут занимать не более двух электронов. Для объяснения электрических, тепловых, оптических свойств достаточно рассматривать две высшие зоны: валентную зону, образованную расщеплением основного уровня энергии валентных электронов, и зону проводимости, образованную расщеплением уровня энергии возбужденных электронов.
Для объяснения электрических, тепловых, оптических свойств достаточно рассматривать две высшие зоны: валентную зону, образованную расщеплением основного уровня энергии валентных электронов, и зону проводимости, образованную расщеплением уровня энергии возбужденных электронов. Кристалл является проводником, если в валентной зоне есть свободные уровни энергии или она перекрывается с зоной проводимости. Под действием электрического поля электроны и дырки имеют право перемещаться в кристалле с увеличением скорости, занимая все более высокие уровни энергии.
Кристалл является проводником, если в валентной зоне есть свободные уровни энергии или она перекрывается с зоной проводимости. Под действием электрического поля электроны и дырки имеют право перемещаться в кристалле с увеличением скорости, занимая все более высокие уровни энергии. . (1)
. (1) . (2)
. (2)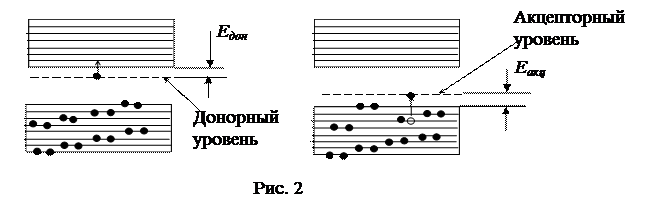
 . (3)
. (3) , (4)
, (4)  . (5)
. (5)
 . Таким образом, можно по графику определить энергию активации. Если она будет около электрон-вольта, то это собственный полупроводник, если доли электрон-вольта, то это примесный полупроводник.
. Таким образом, можно по графику определить энергию активации. Если она будет около электрон-вольта, то это собственный полупроводник, если доли электрон-вольта, то это примесный полупроводник.

 1. В однородной изотропной среде свет распространяется прямолинейно.
1. В однородной изотропной среде свет распространяется прямолинейно. . (1)
. (1) Если свет падает из вакуума на границу с прозрачной средой, то показатель преломления называется абсолютным. Относительный показатель преломления может быть определён как отношение абсолютных показателей преломления
Если свет падает из вакуума на границу с прозрачной средой, то показатель преломления называется абсолютным. Относительный показатель преломления может быть определён как отношение абсолютных показателей преломления  . Чем больше абсолютный показатель преломления, тем среда считается оптически более плотной.
. Чем больше абсолютный показатель преломления, тем среда считается оптически более плотной. , (2)
, (2)
 . (3)
. (3)
 . (1)
. (1) . Для удобства решения задач интерференции полагают, что свет в разных средах распространяется с одинаковой скоростью, равной скорости света в вакууме: с =3 10 8 м/с. Но чтобы время распространения и фаза в точке наблюдения не изменились, увеличивают в
. Для удобства решения задач интерференции полагают, что свет в разных средах распространяется с одинаковой скоростью, равной скорости света в вакууме: с =3 10 8 м/с. Но чтобы время распространения и фаза в точке наблюдения не изменились, увеличивают в  раз его путь. Здесь V – скорость света в среде. Это воображаемое расстояние, равное произведению геометрического пути на показатель преломления, называется оптическим путем L = l n. Соответственно считают, что при той же частоте в n раз увеличилась длина волны λ = λ 1 n 1 = λ 2 n 2 и стала равна длине волны в вакууме.
раз его путь. Здесь V – скорость света в среде. Это воображаемое расстояние, равное произведению геометрического пути на показатель преломления, называется оптическим путем L = l n. Соответственно считают, что при той же частоте в n раз увеличилась длина волны λ = λ 1 n 1 = λ 2 n 2 и стала равна длине волны в вакууме. Оптическая разность хода отраженных лучей 1 и 2 возникает потому, что луч 2, после разделения с лучом 1 в точке А, дважды проходит расстояние d между линзой и пластинкой и еще теряет полволны при отражении от пластинки. Путь луча 1 от точки разделения А до фронта АВ равен нулю. Разность оптических путей будет равна
Оптическая разность хода отраженных лучей 1 и 2 возникает потому, что луч 2, после разделения с лучом 1 в точке А, дважды проходит расстояние d между линзой и пластинкой и еще теряет полволны при отражении от пластинки. Путь луча 1 от точки разделения А до фронта АВ равен нулю. Разность оптических путей будет равна . (4)
. (4)


