
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение резонансного потенциала атомаСодержание книги
Поиск на нашем сайте
Планетарная модельатома, предложенная Резерфордом на основании опытов по облучению веществ a −частицами, представляет атом состоящим из маленького, но массивного ядра и электронов, вращающихся вокруг ядра. Согласно классической электродинамике электрон, вращаясь с центростремительным ускорением, должен излучать электромагнитные волны. Спектр излучения должен быть сплошным, так как из-за потерь энергии на излучение электрон должен приближаться к ядру с увеличением частоты и упасть на ядро. На самом деле атомы вечны и спектр излучения газов не сплошной, а линейчатый. Первая неклассическая теория атома была предложена Бором введением постулатов, ограничивающих состояние электрона в атоме. Первый постулат: электроны в атоме могут двигаться только по определенным стационарным орбитам, находясь на которых они не излучают энергии. В стационарном состоянии атома электрон, двигаясь по орбите, должен иметь квантованные значения момента импульса, кратные постоянной Планка, деленной на 2 p:
где r и V – радиус орбиты электрона и его скорость, n = 1, 2, 3,... – главное квантовое число, h = 6,63 10 -34 Дж∙с – постоянная Планка. Второй постулат Бора: при переходе атома из одного стационарного состояния в другое испускается или поглощается один квант энергии. Атом излучает квант энергии в виде цуга электромагнитной волны, названный фотоном, если электрон переходит с более высокой орбиты m на более низкую n. Энергия фотона равна разности уровней энергии: hn = Wm – Wn. (2)
Постулаты Бора – это гениальная догадка, они не следуют из законов классической физики. Только с созданием квантовой механики было показано, что они являются следствием решения уравнения Шредингера для атома. Применение второго постулата Бора и уравнения второго закона Ньютона к атому водорода позволило получить формулы и доказать дискретность радиусов стационарных орбит, скоростей и, главное, дискретность значений энергии электрона. Состояние с самой низкой энергией называется основным, все остальные называются возбужденными. Наиболее высокое значение энергии соответствует свободному, не связанному с ядром, электрону. Ее принимают равной нулю, а энергия других состояний отрицательна. Чтобы удалить электрон из атома, ему надо сообщить энергию ионизации, численно равную энергии основного состояния. Ионизация атома может происходить при поглощении кванта электромагнитного излучения, или электронным ударом. При электронном ударе некоторый электрон, получив кинетическую энергию в электрическом поле еφ, при соударении с атомом выбивает его электрон.Происходит ионизация атома, если При меньшем значении энергии, чем энергия ионизации, возможно два типа соударений электрона с атомом. Неупругое соударение происходит, если энергия электрона равна, или достаточно близка, к разности энергий одного из возбужденных состояний и основным состоянием атома. В этом случае атом может принять энергию электрона, происходит резонансное поглощение энергии, и атом переходит в возбужденное состояние. А электрон теряет свою энергию и скорость. Обратный переход возбужденного атома в основное состояние совершается сбросом энергии в виде излучения. Если энергия электрона больше или меньше энергии резонансного поглощения, то соударение электрона с атомом происходит упруго. Без потери энергии электрон отлетает от атома.
Экспериментальное определение резонансных потенциалов было проведено Франком и Герцем. В электронной лампе, откачанной до глубокого вакуума, с небольшим количеством паров ртути, были расположены электроды (рис. 1). Источником электронов являлся накаливаемый катод. В регулируемом электрическом поле между катодом и первой сеткой электроны разгонялись. В пространстве между сетками происходили соударения электронов с атомами ртути. Между второй сеткой и анодом было создано постоянное сравнительно слабое тормозящее поле. Если происходило неупругое взаимодействие электронов с атомами, то они теряли кинетическую энергию и не могли попасть на анод через тормозящее поле. Сила тока между анодом и катодом резко падала. Если ускоряющее напряжение между катодом и сеткой отличалось от резонансного потенциала, то электроны преодолевали тормозящее поле и попадали на анод. Сила тока возрастала. Сила тока могла падать при ускоряющем напряжении, превышающем потенциал возбуждения в два, три и более раз, так как могло происходить два, три и более соударений. Характерная вольтамперная характеристика лампы имеет вид кривой с несколькими максимумами тока и минимумами (рис. 2). Номер минимума равен числу соударений электронов. Установка для изучения опыта Франка – Герца (рис. 3) состоит из газонаполненного (криптоном) триода. От блока питания подается пилообразное напряжение между катодом и сеткой (0–40 В) и тормозящее постоянное напряжение между сеткой и анодом. Анодный ток лампы после преобразования в напряжение подается на вертикальный вход осциллографа. На горизонтальный вход подается пилообразное напряжение для развертки луча. За один период роста напряжения электроны успевают испытать одно, два и более соударений.
ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ КЮРИ Вещество состоит из атомов. Движение электрона в атоме можно представить в виде замкнутого электрического тока. Этот ток создает свое магнитное поле и обладает некоторым магнитным моментом. Определим магнитный момент атома, основываясь на теории Бора. Пусть электрон движется по круговой орбите радиуса r со скоростью V. Магнитный момент орбитального движения электрона равен произведению силы тока (равной отношению заряда электрона к периоду обращения) на площадь орбиты Кроме орбитального магнитного момента электрон обладает еще спиновым магнитным моментом. Результирующий магнитный момент атома равен векторной сумме орбитальных и спиновых магнитных моментов. В парамагнетиках и ферромагнетиках магнитный момент атома обычно равен нескольким магнетонам Бора. Только в диамагнетиках магнитные моменты электронов скомпенсированы. Намагничивание веществ обусловлено действием магнитного поля на магнитные моменты атомов. В магнитном поле на магнитные моменты атомов действует момент силы М = рm В sin a, который стремится установить векторы магнитных моментов атомов в направлении вектора индукции В магнитного поля. Этот процесс называется намагничиванием. Характеристикой является намагниченность, равная векторной сумме магнитных моментов атомов в единице объема: В = m m 0 Н. (1)
Здесь m 0 = 4p∙10 –7 Гн/м – магнитная постоянная, m – относительная магнитная проницаемость. Она характеризует способность веществ намагничиваться и равна отношению индукции поля в веществе к индукции μ 0 H внешнего поля Ферромагнетики – это вещества, способные очень сильно намагничиваться. Магнитная проницаемость достигает сотен тысяч единиц. К ферромагнетикам относятся железо, никель, кобальт, их сплавы. Для атомов ферромагнетиков характерно то, что внешняя электронная оболочка заполнена, а внутренняя 3d – недостроена. Поэтому из-за более сильного так называемого обменного взаимодействия между атомами энергетически выгоднее параллельная ориентация магнитных моментов атомов даже в отсутствие внешнего магнитного поля. Но если во всем объеме ферромагнетика магнитные моменты атомов самопроизвольно установятся параллельно, то он будет сильнейшим постоянным магнитом. Этого не наблюдается, за исключением мелких крупинок. Объясняется это тем, что объем ферромагнетика разделяется на небольшие области самопроизвольного намагничивания так, что их магнитные поля замыкаются. Энергия магнитного поля становится минимальной. Эти области самопроизвольного намагничивания называются домены. Размеры доменов 0,1–1мкм.
Температурная зависимость намагниченности обусловлена влиянием теплового движения атомов на их обменное взаимодействие. При температуре абсолютного нуля магнитные моменты атомов внутри домена параллельны, и намагниченность максимальна. С ростом температуры упорядоченная ориентация магнитных моментов атомов нарушается. При некоторой температуре, называемой температурой Кюри, когда энергия теплового движения атомов становится сравнимой с энергией обменного взаимодействия, упорядоченность исчезает. Ферромагнетик переходит в парамагнитное состояние. У железа температура Кюри 770 °С, у никеля 358 °С, у ферритов 100–200 оС. Исследование температурной зависимости магнитной проницаемости ферромагнетика выполняется на установке (рис.2). Исследуемое ферритовое кольцо находится внутри электронагревателя. На кольце имеются две катушки. По первичной катушке протекает переменный ток силой I, который создаёт магнитное поле с напряженностью
Здесь l – длина средней линии сердечника, N 1– число витков первичной катушки, w – циклическая частота переменного тока. Переменное магнитное поле создает во вторичной катушке ЭДС электромагнитной индукции. По закону Фарадея ЭДС равна скорости изменения магнитного потока через все витки:
Здесь N 2 – число витков вторичной катушки, S –- площадь поперечного сечения сердечника. Среднее значение магнитной проницаемости может быть рассчитано по формуле
 , ,  , (4) , (4)
где
|
|||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 396; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.37.178 (0.01 с.) |

 , (1)
, (1) . Так называемый потенциал ионизации равен отношению энергии основного состояния к заряду электрона
. Так называемый потенциал ионизации равен отношению энергии основного состояния к заряду электрона  .
.
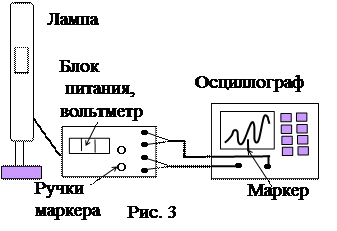 В результате сила тока испытает несколько падений и вольтамперная характеристика триода примет вид, как на рис. 2. Блок питания формирует сигнал маркера, который можно перемещать по экрану. По горизонтальной координате маркера цифровой вольтметр показывает соответствующее напряжение.
В результате сила тока испытает несколько падений и вольтамперная характеристика триода примет вид, как на рис. 2. Блок питания формирует сигнал маркера, который можно перемещать по экрану. По горизонтальной координате маркера цифровой вольтметр показывает соответствующее напряжение. , где период равен
, где период равен  . Радиус орбиты и скорость неизвестны. Их можно исключить, так как они входят в выражение момента импульса, который, согласно постулату Бора, равен
. Радиус орбиты и скорость неизвестны. Их можно исключить, так как они входят в выражение момента импульса, который, согласно постулату Бора, равен  , г де h – постоянная Планка, n = 1, 2, … – квантовое число. Тогда магнитный момент электрона будет равен
, г де h – постоянная Планка, n = 1, 2, … – квантовое число. Тогда магнитный момент электрона будет равен  , где
, где  = 9,02∙10 –23 Дж с /кг – магнетон Бора.
= 9,02∙10 –23 Дж с /кг – магнетон Бора. . Атомы создают внутреннее магнитное поле μ 0 J, которое складывается с внешним μ 0 Н полем:
. Атомы создают внутреннее магнитное поле μ 0 J, которое складывается с внешним μ 0 Н полем:  . В однородном веществе индукция магнитного поля связана с напряженностью соотношением
. В однородном веществе индукция магнитного поля связана с напряженностью соотношением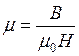 . В парамагнетиках магнитная проницаемость чуть больше единицы, а в диамагнетиках чуть меньше единицы.
. В парамагнетиках магнитная проницаемость чуть больше единицы, а в диамагнетиках чуть меньше единицы. Так как домены уже намагничены до насыщения, то внешнему магнитному полю нет необходимости, как в парамагнетиках, преодолевать тепловое движение.
Так как домены уже намагничены до насыщения, то внешнему магнитному полю нет необходимости, как в парамагнетиках, преодолевать тепловое движение.  Доста-точно даже слабого магнитного поля, чтобы граница между доменами начала смещаться, увеличивая объем тех доменов, намагниченность которых близка к направлению поля, которые находятся в энергетически выгодном состоянии. Поэтому намагниченность и магнитная проницаемость
Доста-точно даже слабого магнитного поля, чтобы граница между доменами начала смещаться, увеличивая объем тех доменов, намагниченность которых близка к направлению поля, которые находятся в энергетически выгодном состоянии. Поэтому намагниченность и магнитная проницаемость  быстро возрастают (рис. 1). В средних и сильных полях начинается процесс вращения магнитных моментов атомов по направлению к магнитному полю. После этого намагниченность ферромагнетиков достигает насыщения.
быстро возрастают (рис. 1). В средних и сильных полях начинается процесс вращения магнитных моментов атомов по направлению к магнитному полю. После этого намагниченность ферромагнетиков достигает насыщения. . (2)
. (2) . (3)
. (3) . Подставив сюда значение амплитуд индукции из (3) и напряженности из (2), получим
. Подставив сюда значение амплитуд индукции из (3) и напряженности из (2), получим
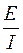 – отношение эффективных значений ЭДС и силы тока, измер
– отношение эффективных значений ЭДС и силы тока, измер


