
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение массы радиоактивного препаратаСодержание книги
Поиск на нашем сайте
Радиоактивностью называется явление самопроизвольного распада атомных ядер с превращением одних ядер в другие, сопровождаемое испусканием элементарных частиц. Распад испытывают нестабильные ядра. Энергия, выделяющаяся при распаде, очень велика (несколько МэВ) и может быть определена по соотношению Эйнштейна как произведение разности масс покоя исходного ядра и продуктов распада на квадрат скорости света Существует несколько видов радиоактивного распада. При альфа - распаде из ядер вылетают α -частицы. Они обладают двойным положительным элементарным зарядом, а их масса составляет 4 атомных единицы. То есть это ядра гелия, состоящие из двух протонов и двух нейтронов. Испытывают α- распад в основном ядра тяжелых элементов, стоящих в таблице Менделеева за свинцом. Образовавшиеся ядра также могут быть радиоактивными, поэтому возникает цепочка распадов, заканчивающаяся на изотопах свинца и на висмуте. Существует 4 радиоактивных семейства с массовыми числами 4 n, 4 n+ 14 n+ 24 n+ 3. Если материнское ядро X испытывает α -распад, то онопревращается в дочернее ядро Y, стоящее в таблице Менделеева на две клеточки ближе к началу, с массовым числом меньше на 4 единицы:
Кинетическая энергия α- частиц принимает дискретные значения, что свидетельствует о дискретности энергетических уровней ядер. Бета-распад происходит при распаде ядер с вылетом электрона или позитрона. Бывает, что ядро захватывает один из ближайших электронов с электронной оболочки и испытывает β- превращение. Кроме того, при электронном β- распаде из ядра вылетает еще антинейтрино, а при позитронном – нейтрино. Нейтрино – это элементарная частица без электрического заряда, масса покоя которой, возможно, равна нулю. Уравнение, например, электронного распада имеет вид
При электронном бета-распаде дочернее ядро смещается на одну клеточку к концу таблицы Менделеева, при позитронном распаде – на одну клеточку к началу таблицы. Спектр энергии β- частиц− сплошной, так как некоторую, неопределенную часть энергии уносят нейтрино. Альфа- и бета-распады сопровождаются гамма-излучением. Это жесткое, коротковолновое электромагнитное излучение с огромной энергией до нескольких МэВ, с большой проникающей способностью. Оно обусловлено излучением дочернего ядра, которое после распада оказалось в возбужденном состоянии, при переходе его в основное состояние. Получим уравнение закона радиоактивного распада. Распад ядра – это явление случайное, независимое от других ядер, от внешних воздействий (нагрев, электрические поля). Поэтому, согласно теории вероятности, число распавшихся за небольшой промежуток времени ядер пропорционально времени наблюдения и числу радиоактивных ядер:
Здесь λ – постоянная распада, имеющая определенное значение для каждого радиоактивного изотопа. Она равна величине, обратной среднему времени жизни радиоактивного ядра. Знак минус показывает, что число нераспавшихся ядер N уменьшается. Чтобы определить закон уменьшения числа ядер за достаточно большое время, проинтегрируем уравнение (1) по времени от нуля до некоторого момента t:
Активностью называется число распадов в единицу времени. Из уравнения (1) По известной активности можно определить число радиоактивных ядер и, значит, массу препарата. Число ядер в определенной массе вещества можно установить по закону Авагадро, согласно которому в одном моле любого вещества содержится одинаковое число атомов, равное NA = 6,02 ∙1023 1/моль. Тогда
Исследуемый радиоактивный препарат плутония Pu239 небольшой массы находится в свинцовом контейнере установки. Измерение активности производится с помощью счетчика Гейгера, подключенного к пересчетному прибору (рис. 2). Счетчик Гейгера представляет собой тонкостенную металлическую трубку, наполненную газом при низком давлении. Трубка является катодом, а анодом служит тонкая нить, натянутая по оси трубки. Между ними приложено напряжение 400–1000 В. При пролете внутри трубки γ -фотона, α-, β- частиц, вследствие ионизации молекул газа, возникают электроны и положительные ионы.
Однако не каждая частица, пролетающая через счетчик Гейгера, вызывает лавинный разряд, а только малая доля, менее процента. Это учитывается коэффициентом, который называется эффективностью счетчика ε. Кроме того, радиоактивное излучение изотропно, распространяется в полном телесном угле 4 π стерадиан, а на счетчик Гейгера попадает только часть излучения, равная отношению видимой площади счетчика S к площади сферы с радиусом, равным расстоянию от препарата до счетчика:
Здесь n – число импульсов, зарегистрированных за время счета t, С – постоянная установки.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.75.217 (0.006 с.) |

 .
. . (1)
. (1)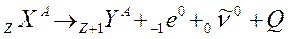 . (2)
. (2) . (1)
. (1) . В результате получим, что число нераспавшихся ядер уменьшается со временем наблюдения от начального числа N 0 по экспоненциальному закону (рис. 1):
. В результате получим, что число нераспавшихся ядер уменьшается со временем наблюдения от начального числа N 0 по экспоненциальному закону (рис. 1): . (2)
. (2) Время, в течение которого распадается половина исходного числа ядер, называется периодом полураспада. По этому условию
Время, в течение которого распадается половина исходного числа ядер, называется периодом полураспада. По этому условию  . Откуда получим соотношение
. Откуда получим соотношение  . Период полураспада известных ядер находится в пределах от 10–7секунды до 1015 лет. Чем меньше период полураспада, тем выше активность препарата.
. Период полураспада известных ядер находится в пределах от 10–7секунды до 1015 лет. Чем меньше период полураспада, тем выше активность препарата. . Единицей активности является беккерель (Бк), равный одному распаду в секунду.
. Единицей активности является беккерель (Бк), равный одному распаду в секунду. , где M – масса одного моля вещества. Подставив N в формулу активности, получим формулу для расчета массы препарата:
, где M – масса одного моля вещества. Подставив N в формулу активности, получим формулу для расчета массы препарата: . (3)
. (3) Электроны, ускоряясь в сильном электрическом поле около нити, производят вторичную ионизацию молекул. В результате в счетчике возникает лавинный разряд. Чтобы зарегистрировать следующую частицу, разряд следует погасить. Для гашения разряда последовательно со счетчиком включается резистор с большим сопротивлением. В момент разряда на резисторе возникает импульс напряжения, который регистрируется.
Электроны, ускоряясь в сильном электрическом поле около нити, производят вторичную ионизацию молекул. В результате в счетчике возникает лавинный разряд. Чтобы зарегистрировать следующую частицу, разряд следует погасить. Для гашения разряда последовательно со счетчиком включается резистор с большим сопротивлением. В момент разряда на резисторе возникает импульс напряжения, который регистрируется. . Это так называемая геометрическая поправка. Таким образом, скорость счета импульсов в установке меньше активности препарата:
. Это так называемая геометрическая поправка. Таким образом, скорость счета импульсов в установке меньше активности препарата:  . С учетом поправок формула (3) примет вид
. С учетом поправок формула (3) примет вид . (4)
. (4)


