
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение ширины щели и экранаСодержание книги
Поиск на нашем сайте
Дифракция света – это явление огибания светом препятствий, захождение света в область геометрической тени. Дифракция света обусловлена волновой природой света. Распределение интенсивности света в дифракционной картине объясняется принципом Гюйгенса – Френеля: каждая точка среды, до которой дошел волновой фронт, является источником вторичных волн, результат интерференции вторичных волн с учетом их фаз и амплитуд, определяет результирующее колебание в точках наблюдения. То есть дифракция – это явление интерференции вторичных волн. Приближенное решение задач дифракции осуществляется методом зон Френеля. Поверхность фронта волны делят на отдельные зоны так, чтобы оптическая разность хода волн от соседних зон до точки наблюдения была равна половине длины волны. В этом случае волны от соседних зон ослабляют друг друга полностью или частично. Если на поверхности фронта уложится четное число зон Френеля, то в точке наблюдения будет минимум освещенности. Если число зон будет нечетное, то свет одной из зон будет не скомпенсирован и в точке наблюдения будет максимум. Рассмотрим две задачи дифракции: на щели и на узком экране. Пусть параллельный пучок света падает нормально на поверхность щели. Каждая точка поверхности щели становится источником вторичных волн, распространяющихся в пределах от –90о до + 90о. Разделим поверхность щели на зоны Френеля. Для этого проведем систему плоскостей, расстояние от которых до точки наблюдения возрастает на половину длины волны (рис. 1). Они разрезают поверхность щели на систему узких полосок, которые являются зонами Френеля.
 . Из треугольника (рис. 1) разность хода крайних лучей равна D L = b sin a. Здесь b – ширина щели, a – угол дифракции. Тогда условие минимума примет вид . Из треугольника (рис. 1) разность хода крайних лучей равна D L = b sin a. Здесь b – ширина щели, a – угол дифракции. Тогда условие минимума примет вид
b sin a = m l. (1)
В центре дифракционной картины расположен центральный максимум. Для него щель является одной зоной Френеля. Он является изображением щели. Ширина изображения равна расстоянию между первыми минимумами: Н = 2 F tg a. Если тангенс малого угла a заменить синусом этого угла из (1), то получим для ширины изображения щели
В стороне от центра экрана волны от полосок приходят с разностью фаз D j и векторная диаграмма закручивается в спираль. Для ближайшего максимума первого порядка спираль должна сделать полтора оборота той же длины Е 0. То есть ее диаметр следует определить из этого равенства Рассмотрим дифракцию параллельного пучка света наузком экране. Поместим в пучок параллельного света преграду в виде узкого экрана шириной d, например тонкую проволочку или волос. Вследствие дифракции света на экране возникнет дифракционная картина. В центре вместо геометрической тени будет центральный максимум, так как волны от вторичных источников на открытых участках фронта огибая экран приходят в одной фазе. Его размер равен сечению пучка света.
Применим метод векторных диаграмм. Пусть векторы амплитуд волн от нечетных зон направлены на диаграмме вверх, а от четных зон (в противофазе) – вниз (рис. 4). Для наглядности растянем векторную диаграмму в «гармошку». Амплитуды колебаний от крайних левых и правых зон меньше, так как зоны расположены дальше от точки наблюдения, либо интенсивность пучка на краях слабее. Результирующая амплитуда равна длине вектора, проведенного из начала первого вектора амплитуды крайней левой зоны в конец последнего от крайней правой зоны. Если препятствия нет, все зоны открыты, то в стороне от центрального максимума будет практически темно. Пусть непрозрачный экран перекрывает одну или нечетное число зон Френеля. Тогда на векторной диаграмме исчезнет нечетное число векторов и при построении диаграммы два вектора от зон у краев экрана окажутся в одной фазе. Результирующая амплитуда возрастет (Е ∞– Е 1). Этому максимуму соответствует нечетное число полуволн в оптической разности хода лучей от краев экрана: Δ L= (2 m + 1) l 2. Из треугольника (рис. 3) Δ L = d sin a. Угловое положение максимума определится формулой
d sin a = (2 m + 1) l 2. (2)
Если перекрыто четное число зон Френеля, то результирующая амплитуда будет минимальна, как и при всех открытых зонах. Расстояние между соседними максимумами на экране наблюдения, отстоящего на фокусном расстоянии линзы F, будет H ≈ F (sin am+1 – sin αm), или В лабораторной установке источником монохроматического излучения является полупроводниковый лазер. На пути пучка света помещаются обоймы либо со щелью переменной ширины, либо с тонким проводом. Испытав дифракцию, свет попадает на экран наблюдения со шкалой.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.93.242 (0.01 с.) |


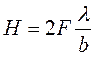 . Изображение тем шире, чем уже щель.
. Изображение тем шире, чем уже щель. Боковые максимумы, по сравнению с центральным максимумом, очень слабые. Для доказательства разделим щель на более узкие полоски, чем зоны Френеля. В центр экрана волны от этих полосок приходят в одной фазе, и векторная диаграмма сложения амплитуд ε от полосок имеет вид прямой линии, Е 0 = ε n (рис. 2).
Боковые максимумы, по сравнению с центральным максимумом, очень слабые. Для доказательства разделим щель на более узкие полоски, чем зоны Френеля. В центр экрана волны от этих полосок приходят в одной фазе, и векторная диаграмма сложения амплитуд ε от полосок имеет вид прямой линии, Е 0 = ε n (рис. 2).
 . Интенсивность, пропорциональная квадрату амплитуды Е 1, составит 4 % от интенсивности центрального максимума.
. Интенсивность, пропорциональная квадрату амплитуды Е 1, составит 4 % от интенсивности центрального максимума. Рассмотрим некоторую точку В, расположенную под углом α к оси пучка в стороне от центрального максимума (рис. 3). Разделим фронт пучка света на зоны Френеля плоскостями так, чтобы оптический путь от соседних зон изменялся на λ / 2. Пучок должен быть небольшого сечения, около миллиметра, однако число зон Френеля будет очень велико.
Рассмотрим некоторую точку В, расположенную под углом α к оси пучка в стороне от центрального максимума (рис. 3). Разделим фронт пучка света на зоны Френеля плоскостями так, чтобы оптический путь от соседних зон изменялся на λ / 2. Пучок должен быть небольшого сечения, около миллиметра, однако число зон Френеля будет очень велико.
 . (3)
. (3)


