
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение электронно-дырочного переходаСодержание книги
Поиск на нашем сайте
Электронно-дырочный переход, или p-n переход, – это область контакта двух полупроводников с различным типом проводимости: р -типа и n -типа. Чистый полупроводник при температуре абсолютного нуля является изолятором. При нагреве возможна ионизация атомов полупроводника с образованием свободного электрона и дырки. Дырка – это вакантная, незаполненная химическая связь между атомами. Она может быть заполнена электроном соседнего атома, затем следующего. Перемещение дырки по кристаллу эквивалентно движению положительного элементарного заряда. В чистом полупроводнике число свободных электронов равно числу дырок, они являются носителями заряда. Внесение ничтожных долей примеси в сверхчистый кристалл полупроводника изменяет тип проводимости. Полупроводник n -типа можно получить, если в кристалл 4-валентного, например германия, добавить небольшое количество 5-валентной примеси, например фосфора. Один валентный электрон атома примеси окажется слабо участвующим в химической связи. Его сравнительно легко оторвать от атома за счёт энергии теплового движения. Поэтому в полупроводниках n -типа электронов больше, чем дырок, и они являются основными носителями заряда, а дырки – неосновными носителями. Полупроводник р -типа можно получить, если в кристалл 4-валентного сверхчистого полупроводника добавить небольшое количество трёхвалентной примеси, например индия. Одна химическая связь атома примеси оказывается незаполненной, то есть дыркой. При ионизации собственных атомов полупроводника также образуются дырки и электроны. Дырок в полупроводнике р -типа больше, чем электронов, и они являются основными носителями электрического заряда, а электроны – неосновными. При образовании контакта полупроводников с разным типом проводимости, вследствие теплового движения электроны из n- полупроводника, где их много, диффундируют в р- полупроводник. Там они рекомбинируют, то есть заполняют вакантные связи, создавая отрицательно заряженный ион из атома примеси. И наоборот, дырки из р- полупроводника диффундируют в n- полупроводник, где они рекомбинируют с электронами с образованием положительного иона примеси. В результате около зоны контакта свободных зарядов ставится мало, а образовавшиеся в узлах кристаллической решетки ионы разного знака создают двойной электрический слой с так называемой контактной разностью потенциалов, Uк. Электрическое поле двойного электрического слоя препятствует дальнейшей диффузии основных носителей заряда. Для них возникает потенциальный барьер (рис.1). Его смогут преодолеть только те заряды, энергия теплового движения которых превышает барьер. Их концентрация, по уравнению Больцмана, растет с увеличением температуры:
Здесь е – заряд электрона, k – постоянная Больцмана, Т – температура, J 0 – сила тока, если бы все заряды переходили через барьер. Зато контактное поле не препятствует, а, наоборот, увлекает неосновные носители заряда. Их движение создаёт ток дрейфа, противоположный току диффузии. В отсутствии внешних электрических полей устанавливается динамическое равновесие: ток дрейфа понижает барьер, а встречный ток диффузии его восстанавливает Jдр = Jдиф. Электрическое поле, приложенное к электронно-дырочному переходу, нарушает равновесие. При прямом включении на кристалл р -типа подают положительный потенциал, а на кристалл n -типа – отрицательный (рис. 1, прямое). Внешнее поле при этом ослабляет контактное поле, понижает высоту потенциального барьера, и ток диффузии основных носителей возрастает. А ток дрейфа неосновных носителей остаётся постоянным. Результирующая сила тока определяется разностью тока диффузии и тока дрейфа:
Коэффициент перед скобкой имеет смысл тока дрейфа. Поэтому формулу (2) можно переписать в виде
 . (3) . (3)
Если к электронно-дырочному переходу приложить обратное, запирающее напряжение, то внешнее поле усиливает контактное поле (рис. 1, обратное). Возрастает высота потенциального барьера. Ток диффузии основных носителей быстро падает практически до нуля. Остаётся постоянный по величине ток дрейфа, направленный от n -кристалла к р -кристаллу. Силу обратного электрического тока можно также определить по формуле (3), только полагая внешнее напряжение отрицательным. Вольтамперная характеристика электронно-дырочного перехода, то есть зависимость силы тока от приложенного напряжения определяется теоретически уравнением (3). С ростом прямого напряжения результирующая сила тока растёт сначала медленно, пока внешнее напряжение не превысит контактное. Затем происходит быстрый рост силы тока, практически по экспоненциальному закону, так как током дрейфа (единицей в скобке уравнения 3) можно пренебречь. Таким образом, вольтамперная характеристика электронно-дырочного перехода является нелинейной: прямой ток большой, а обратный меньше в тысячи раз (рис. 2). Это свойство используется в полупроводниковых диодах для выпрямления переменного тока.
ОПРЕДЕЛЕНИЕ кОНЦЕНТРАЦИИ ЭЛЕКТРОНОВ
Классическая электронная теория электропроводности предполагает, что в проводниках есть свободные электроны, которые ведут себя подобно идеальному газу. Количество свободных электронов примерно равно числу атомов. При включении электрического поля на тепловое движение накладывается дрейф – направленное движение под действием сил поля. Из-за рассеяния электронов на ионах в узлах кристаллической решетки происходит потеря кинетической энергии электронов с превращением в теплоту и возникает электрическое сопротивление. Электронная теория Друде−Лоренца подтверждает экспериментальные законы постоянного тока – закон Ома, закон Джоуля – Ленца. Но удельная проводимость σ оказываетсяна один-два порядка меньше экспериментальных значений. Объяснение дано в квантовой механике в зонной теории твердых тел. При образовании кристалла из N отдельных атомов дискретные уровни энергии валентных электронов расщепляются на N уровней вследствие взаимодействия электрона со всеми атомами проводника. Расщепленные уровни образуют энергетические зоны, обычно отделенные друг от друга. Для объяснения электропроводности достаточно рассмотреть две верхние зоны: валентную зону, образованную из основного энергетического уровня валентных электронов, и зону проводимости свободных электронов. По принципу Паули на каждом энергетическом уровне может находиться не более двух электронов с противоположным направлением спина (собственного момента импульса). При температуре абсолютного нуля электроны заполняют попарно энергетические уровни, поднимаясь по уровням все выше. Наивысший занятый уровень энергии называется уровнем Ферми. Энергия Ферми Е Ф имеет значение 5–8 эВ. Это большая энергия, она соответствует энергии теплового движения при температуре более 10 000 К. Поэтому при нагреве (кТ<<Е Ф ) распределение электронов по энергиям изменяется для малой доли, менее процента, вблизи уровня Ферми (рис. 1). Если валентная зона заполнена не полностью, либо перекрывается с зоной проводимости, то в этом случае электроны верхних уровней под действием электрического поля имеют право увеличивать кинетическую энергию, переходя на свободные уровни, перемещаться по кристаллу и переносить ток. Электроны из нижних уровней в электропроводности не участвуют. То есть в отличие от
классической теории только малая часть валентных электронов переносит электрический ток. Если валентная зона отделена от зоны проводимости так называемой запрещенной зоной, но небольшая часть электронов под действием теплового движения сможет преодолеть ее, то эти электроны становятся носителями тока. Когда при ионизации электрон отрывается от атома, он оставляет незаполненную химическую связь. Соответственно в валентной зоне остается не занятый энергетический уровень – «дырка», на который может перейти другой электрон, оставив после себя тоже дырку, которую займет следующий электрон и т. д. Перемещение дырки по кристаллу эквивалентно движению положительного заряда. Таким образом, возникает еще один тип носителей зарядов, о которых не знает классическая теория. Тела могут обладать как электронной, так и дырочной проводимостью или обеими вместе. Для изучения вида и знака носителей заряда в твердых телах можно применить эффект Холла. Он состоит в появлении поперечной разности потенциалов в проводнике с током, помещенном в магнитное поле. Причиной этого является действие силы Лоренца на движущиеся заряды Пусть по образцу в форме прямоугольной пластинки размерами d,l,c течет ток (рис. 2). Если носители заряда положительные, то под действием силы Лоренца они отклонятся на левую грань пластинки (рис. 2а). Если носители зарядов отрицательные, то, наоборот, на левую грань отклонятся отрицательные заряды (рис. 2б). В обоих случаях возникают поперечные электрические поля, но полярность будет различна. Это позволяет определить знак носителей зарядов. Возникающее поперечное электрическое поле препятствует последующему отклонению электрических зарядов. Накопление зарядов на гранях прекратится и наступит равновесие, когда сила Лоренца будет уравновешена силой возникшего электрического поля
Напряженность поперечного поля
Получим формулу для определения концентрации зарядов. От концентрации зарядов зависит сила тока. По определению силы тока суммарный заряд, прошедший через сечение проводника, равен произведению силы тока на время движения:
по которой можно определить концентрацию носителей зарядов. Экспериментальное изучение эффекта Холла производится на пластинке полупроводника, помещенной в зазор электромагнита. Силу тока и ЭДС Холла определяют по индикаторам цифровых милливольтметра и миллиамперметра электронного блока. Индукцию магнитного поля рассчитывают по силе тока катушки электромагнита: B= 2,21 Jмагн.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

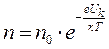 . Они создают ток диффузии
. Они создают ток диффузии . (1)
. (1) . (2)
. (2)


 . Ее направление можно определить правилом левой руки. Если четыре пальца руки направлены по току, а силовые линии входят в ладонь, то отогнутый большой палец укажет направление силы Лоренца.
. Ее направление можно определить правилом левой руки. Если четыре пальца руки направлены по току, а силовые линии входят в ладонь, то отогнутый большой палец укажет направление силы Лоренца. . (1)
. (1) . ЭДС Холла равна разности потенциалов между боковыми гранями и равна произведению напряженности на длину силовых линий:
. ЭДС Холла равна разности потенциалов между боковыми гранями и равна произведению напряженности на длину силовых линий: 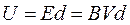 . Отсюда можно по известной ЭДС определить среднюю скорость дрейфа зарядов
. Отсюда можно по известной ЭДС определить среднюю скорость дрейфа зарядов
 . (2)
. (2) . Суммарный заряд всех носителей внутри пластинки равен произведению концентрации зарядов на величину элементарного заряда е и на объем образца:
. Суммарный заряд всех носителей внутри пластинки равен произведению концентрации зарядов на величину элементарного заряда е и на объем образца: 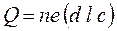 . Время дрейфа зарядов от нижнего торца до верхнего
. Время дрейфа зарядов от нижнего торца до верхнего  . Подставив формулы заряда и времени дрейфа, получим для скорости дрейфа
. Подставив формулы заряда и времени дрейфа, получим для скорости дрейфа  . Подставив скорость дрейфа зарядов V в формулу ЭДС U=BVd, получим для ЭДС формулу
. Подставив скорость дрейфа зарядов V в формулу ЭДС U=BVd, получим для ЭДС формулу , (3)
, (3)


