
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерференция поляризованных волн. Оптическая активность. Искусственная оптическая активность.Содержание книги
Поиск на нашем сайте
Явления интерференции поляризованных лучей исследовались в классических опытах Френеля и Арго (1816 г.), доказавших поперечность световых колебаний. Суть их в зависимости результата интерференции от угла между плоскостями световых колебаний: полосы наиболее контрастны при параллельных плоскостях и исчезают, если волны поляризованы ортогонально. Трудность получения интерференции поляризованных волн состоит в том, что при наложении двух когерентных лучей, поляризованных во взаимно перпендикулярных направлениях, никакой интерференционной картины с максимумами и минимумами интенсивности получиться не может. Интерференция возникает только в том случае, если колебания во взаимодействующих лучах совершаются вдоль одного и того же направления. Колебания в двух лучах, первоначально поляризованных во взаимно перпендикулярных направлениях, можно свести в одну плоскость, пропустив эти лучи через поляризующую кристаллическую пластинку. Рассмотрим схему получения интерференции поляризованных лучей (рис. 11.13).
Рис. 11.13 Прошедшее через поляризатор Р излучение точечного источника S попадает на полуволновую кристаллическую пластинку Q, которая позволяет изменять угол между плоскостями поляризации интерферирующих лучей: ее поворот на угол α поворачивает вектор при прохождении поляризованного света через кристаллическую пластинку разность хода между двумя компонентами поляризации зависит от толщины пластинки, среднего угла преломления и разности показателей
различна для разных длин волн, и тем самым интерференционная картина оказывается окрашенной. Для плоскопараллельных пластинок наблюдаются полосы равного наклона, а для тонких клиновидных пластинок - полосы равной толщины. Приведенная формула позволяет для любой фазовой пластинки рассчитать интенсивность на выходе при скрещенных поляризаторе и анализаторе:
Вопрос 20
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.62.10 (0.006 с.) |


 на 2α. Если наблюдать интерференционные полосы через анализатор А, то при его повороте на π/2 картина, наблюдаемая на экране Э, инвертируется: из-за дополнительной разности фаз π темные полосы становятся светлыми и наоборот. Анализатор здесь необходим также для того, чтобы свести колебания двух различно поляризованных лучей в одну плоскость.
на 2α. Если наблюдать интерференционные полосы через анализатор А, то при его повороте на π/2 картина, наблюдаемая на экране Э, инвертируется: из-за дополнительной разности фаз π темные полосы становятся светлыми и наоборот. Анализатор здесь необходим также для того, чтобы свести колебания двух различно поляризованных лучей в одну плоскость. и
и  . Очевидно, что возникающая при этом разность фаз
. Очевидно, что возникающая при этом разность фаз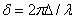
 .
.
 , где
, где  – толщина слоя оптически активного вещества, коэффициент
– толщина слоя оптически активного вещества, коэффициент  называется удельным вращением. В растворах угол поворота плоскости поляризации равен:
называется удельным вращением. В растворах угол поворота плоскости поляризации равен:  , где С – объемно – массовая концентрация оптически активного вещества в растворе,
, где С – объемно – массовая концентрация оптически активного вещества в растворе,  – удельная константа вращения раствора,
– удельная константа вращения раствора,  , отвечает соотношению:
, отвечает соотношению:  , где
, где  – напряженность внешнего магнитного поля;
– напряженность внешнего магнитного поля;  – постоянная Верде, зависящая от природы вещества и длины волны.
– постоянная Верде, зависящая от природы вещества и длины волны.



