
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Когерентность и монохроматичностьСодержание книги
Поиск на нашем сайте Световых волн
Интерференцию света можно объяснить, рассматривая интерференцию волн (см. § 156). Необходимым условием интерференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические волны — не ограниченные в пространстве волны одной определенной и строго постоянной частоты. Так как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. Поэтому на опыте не наблюдается интерференция света от независимых источников, например от двух электрических лампочек. Понять физическую причину немонохроматичности, а следовательно, и некогерентности волн, испускаемых двумя независимыми источниками света, можно исходя из самого механизма испускания света атомами. В двух самостоятельных источниках света атомы излучают независимо друг от друга. В каждом из таких атомов процесс излучения конечен и длится очень короткое время (т ж 10 ~8 с). За это время возбужденный атом возвращается в нормальное состояние и излучение им света прекращается. Возбудившись вновь, атом снова начинает испускать световые волны, но уже с новой начальной фазой. Так как разность фаз между излучением двух таких независимых атомов изменяется при каждом новом акте испускания, то волны, спонтанно излучаемые атомами любого источника света, некогерентны. Таким образом, волны, испускаемые атомами, лишь в течение интервала времени» 10-8 с имеют приблизительно постоянные амплитуду и фазу колебаний, тогда как за больший промежуток времени и амплитуда, и фаза изменяются. Прерывистое излучение света атомами в виде отдельных коротких импульсов называется волновым цугом. Описанная модель испускания света справедлива и для любого макроскопического источника, так как атомы светящегося тела излучают свет также независимо друг от друга. Это означает, что начальные фазы соответствующих им волновых цугов не связаны между собой. Помимо этого, даже для одного и того же атома начальные фазы разных цугов отличаются для двух последующих актов излучения. Следователь но, свет, испускаемый макроскопическим источником, некогерентен. Любой немонохроматический свет можно представить в виде совокупности сменяющих друг друга независимых гармонических цугов. Средняя продолжительность одного цуга tког называется временем когерентности. Когерентность существует только в пределах одного цуга, и время когерентности не может превышать время излучения, т. е. tког < t. Прибор обнаружит четкую интерференционную картину лишь тогда, когда время разрешения прибора значительно меньше времени когерентности накладываемых световых волн. Если волна распространяется в однородной среде, то фаза колебаний в определен ной точке пространства сохраняется только в течение времени когерентности tког. За это время волна распространяется в вакууме на расстояние l ког = ctког, называемое длиной когерентности (или длиной цуга). Таким образом, длина когерентности есть расстояние, при прохождении которого две или несколько волн утрачивают когерентность. Отсюда следует, что наблюдение интерференции света возможно лишь при оптических разностях хода, меньших длины когерентности для используемого источника света. Чем ближе волна к монохроматической, тем меньше ширина Dw спектра ее частот и, как можно показать, больше ее время когерентности tког, следовательно, и длина когерентности l ког. Когерентность колебаний, которые совершаются в одной и той же точке пространства, определяемая степенью монохроматичности волн, называется временной когерентностью. Наряду с временной когерентностью для описания когерентных свойств волн в плоскости, перпендикулярной направлению их распространения, вводится понятие пространственной когерентности. Два источника, размеры и взаимное расположение которых позволяют (при необходимой степени монохроматичности света) наблюдать интерференцию, называются пространственно-когерентными. Радиусом когерентности (или длиной пространственной когерентности) называется максимальное поперечное направлению распространения волны расстояние, на котором возможно проявление интерференции. Таким образом, пространственная когерентность определяется ради усом когерентности. Радиус когерентности
где l — длина волны света, j— угловой размер источника. Так, минимально возможный радиус когерентности для солнечных лучей (при угловом размере Солнца на Земле j» 10-2рад и l» 0,5 мкм) составляет» 0,05 мм. При таком малом радиусе когерентности невозможно непосредственно наблюдать интерференцию солнечных лучей, поскольку разрешающая способность человеческого глаза на расстоянии наилучшего зрения составляет лишь 0,1 мм. Отметим, что первое наблюдение интерференции провел в 1802 г. Т. Юнг именно с солнечным светом, для чего он предварительно пропускал солнечные лучи через очень малое отверстие в непрозрачном экране (при этом на несколько порядков уменьшался угловой размер источника света и тем самым резко увеличивался радиус когерентности (или длина пространственной когерентности)).
Интерференция света
Предположим, что две монохроматические световые волны, накладываюсь друг на друга, возбуждают в определенной точке пространства колебания одинакового направления: х1 = А1cos(wt + j1) и x2 = A2cos(wt + j2).Под х понимают напряженность электрического Еили магнитного Нполей волны; векторы Е и Н колеблются во взаимно перпендикулярных плоскостях (см. § 162). Напряженности электрического и магнитного полей подчиняются принципу суперпозиции (см. § 80 и 110). Амплитуда результирующего колебания в данной точке A2 = A2l + A22 + 2A1A2 cos(j2 - j1)(см. 144.2)). Так как волны когерентны, то cos(j2 - j1)имеет постоянное во времени (но свое для каждой точки пространства) значение, поэтому интенсивность результирующей волны (1~А2)
В точках пространства, где cos(j2 - j1) > 0, интенсивность I > I1 + I2, где cos(j2 - j1) < О, интенсивность I < I1 + I2. Следовательно, при наложении двух (или нескольких) когерентных световых волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других — минимумы интенсивности. Это явление называется интерференцией света. Для некогерентных волн разность (j2 - j1) непрерывно изменяется, поэтому среднее во времени значение cos(j2 - j1) равно нулю, и интенсивность результирующей волны всюду одинакова и при I1 = I2равна 2I1(для когерентных волн при данном условии в максимумах I = 4I1 в минимумах I = 0). Как можно создать условия, необходимые для возникновения интерференции световых волн? Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга, и наблюдается интерференционная картина. Пусть разделение на две когерентные волны происходит в определенной точке О. До точки М, в которой наблюдается интерференционная картина, одна волна в среде с показателем преломления n2прошла путь s1, вторая — в среде с показателем преломления n2— путь s2.Если в точке О фаза колебаний равна wt, то в точке М первая волна возбудит колебание А1cosw(t – s1/v1), вторая волна — колебание А2cosw(t – s2/v2), где v1 = c/n1, v2 = c/n2— соответственно фазовая скорость первой и второй волны. Разность фаз колебаний, возбуждаемых волнами в точке М, равна
(учли, что w/с = 2pv/с = 2pl0 где l0 — длина волны в вакууме). Произведение геометрической длины sпути световой волны в данной среде на показатель n преломления этой среды называется оптической длиной пути L, a D = L2 – L1 — разность оптических длин проходимых волнами путей — называется оптической разностью хода. Если оптическая разность хода равна целому числу длин волн в вакууме
то d = ± 2pm, и колебания, возбуждаемые в точке М обеими волнами, будут происходить в одинаковой фазе. Следовательно, (172.2) является условием интерференционного максимума. Если оптическая разность хода
то d = ±(2m + 1)p, и колебания, возбуждаемые в точке М обеими волнами, будут происходить в противофазе. Следовательно, (172.3) является условием интерференционного минимума.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 642; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |


 (172.1)
(172.1)
 (172.2)
(172.2)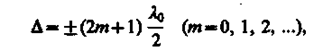 (172.3)
(172.3)


