
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электромагнитные силы. Энергия магнитного поляСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В технике широко применяют устройства, в основе работы которых лежит силовое действие магнитного поля (электродвигатели, реле и контакторы, тяговые и подъемные электромагниты, электроизмерительные приборы и др.). Электромагнитные силы приходится учитывать при расчете электрических аппаратов, проектировании распределительных устройств электрических станций и сетей и т. д. Сила, действующая на проводник с током в магнитном поле. Большой практический интерес представляет выражение электромагнитной силы, действующей на проводник с током I в равномерном магнитном поле с магнитной индукцией В (рис. 4.13). Прямолинейный отрезок провода расположен в пространстве между полюсами постоянного магнита или электромагнита (катушки со стальным сердечником) так, что между направлениями магнитной индукции и тока угол α = 90°. В равномерном магнитном поле на одинаковые элементы длины провода действует одинаковая по величине и направлению электромагнитная сила ΔFм = BIΔ l, что следует из формул (4.1) и (4.2). Рис. 4.13 Сложим элементарные силы по длине l той части провода, которая находится в магнитном поле, получим выражение электромагнитной силы Fм = B I l. (4.24)
При других значениях угла α электромагнитную силу определяют по формуле Fм = B I l sin α, (4.25) где l sin α — проекция отрезка l на направление, перпендикулярное направлению магнитной индукции. Направление электромагнитной силы всегда перпендикулярно плоскости, в которой лежат провод и линии магнитной индукции, но его удобно определить по правилу левой руки: если левую руку расположить так, чтобы линии магнитной индукции «входили» в ладонь, а вытянутые четыре пальца показывали направление тока в проводе, то отогнутый в плоскости ладони большой палец покажет направление электромагнитной силы. Рассмотрим проводящий контур прямоугольной формы, расположенный в равномерном магнитном поле, как показано на рис. 4.14.
Рис. 4.14
При наличии тока I в контуре на его стороны аб и вг действуют электромагнитные силы Fм, которые образуют вращающий момент. Предположим, что ось вращения проходит через середину контура и он поворачивается из положения I в положение II. Некоторое промежуточное положение контура характеризуется углом β, отсчитанным от вертикальной плоскости (в положении I угол β = 0).
Магнитный поток, сцепляющийся с контуром в процессеего поворота, изменяется по такому же закону, по какому изменяется проекция площади контура на плоскость, перпендикулярную линиям магнитной индукции (горизонтальная плоскость): S = l d sin β; Ф = BS = B l dsin β. Обозначив наибольшую величину магнитного потока В l d = Фm (положе-ние II, β = 90°), получим Ф = Фm sin β. В процессе поворота контура при постоянном токе I силы Fм сохраняют свое направление и величину. Одновременно с изменением магнитного потока, сцепляющегося с контуром, изменяется работа электромагнитных сил: ΔA = 2BI l Если проводящий контур содержит не один, а N витков, тогда работа электромагнитных сил увеличивается в N раз, т. е. ΔA = INΔФ. Учитывая, что NΔФ = ΔΨ, получим формулу
ΔА = I ΔΨ. (4.26)
Рассмотренные примеры являются иллюстрацией важных для практики свойств электромагнитных систем: 1. Изменение работы электромагнитных сил или энергии в электромагнитной системе выражается произведением тока и изменения магнитного потокосцепления. 2. Всякий проводящий контур с током в магнитном поле под действием электромагнитных сил стремится занять такое положение, при котором магнитный поток, сцепленный с контуром, будет наибольшим положительным. (При этом положительным считают магнитный поток, совпадающий по направлению внутри контура с потоком созданным током этого контура.) Тяговое усилие электромагнита. Приведенные положения подтверждаются также действием тяговых электромагнитов. Конструкции тяговых электромагнитов (рис. 4.15) разнообразны и определяются их назначением. Но все они имеют намагничивающую обмотку 3, стальной магнитопровод, состоящий из двух частей — неподвижной 1 и подвижной 2. Подвижная часть магнитопровода (якорь) намагничивается в магнитном поле обмотки с током и притягивается к неподвижной части с силой Fм = B2 S/2μ0, (4.27) где В — магнитная индукция, S — площадь сечения полюса.
Магнитный поток при этом достигает наибольшего значения для данной электромагнитной системы, так как воздушныйзазор между сердечником и якорем сокращается, а магнитное сопротивление становится наименьшим.
Рис. 4.15 Рис. 4.16
Силы, действующие на параллельные провода с токами. Параллельное расположение проводов с токами на практике встречается часто: например, при установлении шин распределительных устройств электрических станций и подстанций. Для того чтобы правильно выбрать шины и изоляторы,на которых они закреплены, приходится определять электромагнитные силы, действующие на шины. В подобном случае (рис. 4.16) провод 2 с током I2 находится в магнитном поле тока I1. Магнитная индукция в месте расположения провода 2 В1 = μ0 I1 / 2π а, где а— расстояние между осями проводов. Между направлениями магнитной индукции B1 и током I2 угол 90°, поэтому согласно формуле (4.24) Fм1.2 = В1 I2 t2 = μ0 I1 I2 l 2 / 2 π а. Аналогично можно выразить силу Fм1.2, действующую на провод 1 в магнитном поле провода с током I2. Общее выражение для силы, действующей на равные по длине участки двух проводов, Fм = Свободная заряженная частица в магнитном поле. Действие магнитного поля на заряженные частицы, движущиеся вне проводника, например в вакууме, широко используется в технике. Примерами могут служить фокусировка или смещение электронного пучка (луча) в электроннолучевых трубках телевизоров, осциллографов, электронных микроскопов, ускорение заряженных частиц для исследования ядерных процессов и т. д. Для определения силы, действующей на частицу с зарядом Q, движущуюся в равномерном магнитном поле перпендикулярно направлению магнитной индукции, можно использовать формулу (4.24). Подставим в нее выражение и обозначим скорость движения частицы l / t = υ, получим Fм = BQυ. В данном случае сила Fм согласно правилу левой руки направлена перпендикулярно направлениям магнитной индукции и скорости частицы. Из механики известно, что под действием постоянной по значению силы, направленной перпендикулярно направлению скорости, тело движется по окружности радиуса ρ = mυ2 / Fм = mυ/ QB.
Угловая скорость движения ω0 = υ / ρ = QB / m. Энергия магнитного поля. При возникновении электрического тока в проводящем контуре одна часть энергии источника питания расходуется на преодоление электрического сопротивления контура и превращается в теплоту, другая запасается в виде энергии магнитного поля. С увеличением тока растет энергия магнитного поля. Она может быть возвращена источнику или преобразована в другой вид энергии при уменьшении тока. Для определения энергии магнитного поля воспользуемся формулой (4.26), принимая во внимание, что в процессе установления тока в контуре значение его изменяется от 0 до 1 и вместе с тем изменяется потокосцепление [см. формулу (4.12)]. Следовательно, в формуле (4.26) оба множителя переменные, поэтому она дает основание определить только приращение энергии ΔWм за некоторый весьма малый промежуток времени, в течение которого ток в контуре изменяется на Δ i, а потокосцепление — на ΔΨ. Если индуктивность контура постоянна, то зависимость между потокосцеплением и током изображается прямой линией (рис. 4.17). Изменение энергии при изменении тока на Δ i выражается площадью трапеции (на рисунке заштрихована): ΔWм = i ΔΨ + Δ i ΔΨ/2 ≈ i ΔΨ. Энергию при токе I и потокосцеплении Ψ выражает сумма таких площадок, т. е. площадь S = ΨI/2 прямоугольного треугольника с катетами Ψ, I. Учитывая еще и формулу (4.12), получим три выражения для энергии магнитного поля:
Wм = ΨI / 2 = L I 2/ 2 = Ψ2/2L. (4.29)
Электромагнитная индукция.
Явление электромагнитной индукции состоит в том, что в проводящем контуре возбуждается электродвижущая сила, если магнитный поток, сцепляющийся с этим контуром, изменяется. На основе этого физического явления создаются и работают устройства для взаимного преобразования механической и электрической энергии (электрические генераторы и двигатели), передачи и распределения электрической энергии (трансформаторы, реакторы), передачи и приема информации (радиопередатчики, радиоприемники) и многие другие. Явление и закон электромагнитной индукции необходимо знать также для изучения электрических цепей переменного тока. Явление электромагнитной индукции открыл в 1831 г. английский физик М. Фарадей. В изучение и практическое использование этого явления существенный вклад внесли русские ученые Э. X. Ленц, Б. С. Якоби. Закон электромагнитной индукции. Электродвижущая сила, возбуждаемая в проводящем контуре при изменении сцепленного с ним магнитного потока (индуктированная э.д.с.), количественно определяется по закону электромагнитной индукции. Электродвижущая сила, индуктируемая в проводящем контуре, равна скорости изменения магнитного потока, сцепляющегося с этим контуром е = –d Ф / dt. (4.30) В катушке, имеющей N витков (контуров), э.д.с. в N раз больше, если все витки ее сцеплены с одинаковым потоком е = NdФ /dt, где dФ /dt — скорость изменения магнитного потока. В общем случае витки катушки могут быть сцеплены с разными потоками, тогда общая э.д.с. определяется алгебраической суммой э.д.с. отдельных витков или скоростью изменения общего потокосцепления катушки e = –d Ψ / dt.. (4.31) Знак «минус» в формулах, выражающих э.д.с. электромагнитной индукции, соответствует правилу Ленца: э.д.с., возбуждаемая при изменении магнитного потокосцепления, направлена всегда так, что своим действием препятствует этому изменению. Э.д.с. самоиндукции и взаимоиндукции. При изменении потокосцепления самоиндукции или взаимной индукции также возбуждается э.д.с. Изменение собственного потокосцепления контура (или катушки) обычно является следствием изменения тока в этом же контуре (или катушке).
Индуктированная в данном случае электродвижущая сила называется э.д.с. самоиндукции. Учитывая (4.31) и (4.9), получим eL = –d Ψ1.1 / dt = –Ldi / dt. (4.32) Потокосцепление взаимной индукции изменяется при изменениях тока или коэффициента связи. Выражения э.д.с. взаимоиндукции следуют из формул (4.31) и (4.15) eм1 = –d Ψ2.1 / dt = –Мdi2 / dt, (4.33) e м2 = –d Ψ1.2 / dt = –Мdi1 / dt. (4.34)
Вихревые токи. Примерами использования явления электромагнитной индукции является работа трансформатор,
Рис. 4.18 Рассмотрим металлический сердечник внутри катушки с переменным током (рис. 4.18, а, б). В сердечнике можно мысленно выделить ряд замкнутых слоев, ось которых совпадает с осью сердечника. Каждый такой слой представляет собой замкнутый виток, в котором переменным магнитным потоком индуктируется э.д.с. и возникает ток, замыкающийся в плоскости, перпендикулярной оси магнитного потока. Рассматривая совокупность таких замкнутых контуров, можно представить себе в теле сердечника токи, замыкающиеся вокруг оси магнитного потока (вихревые токи). Направление вихревых токов определяется правилом Ленца. В соответствии с законом Джоуля – Ленца, вследствие вихревых токов выделяется теплота в сердечнике. Это явление используется на практике для нагревания металлов (плавление стали, закалка и др.). В магнитопроводах электрических машин, трансформаторов и электрических аппаратов тоже возникают вихревые токи. Но здесь они нежелательны, так как увеличивают общие потери энергии в устройствах и вызывают дополнительный их нагрев. Э.д.с. в проводнике, движущемся в магнитном поле. В проводнике, движущемся под действием механической силы в магнитном поле так, что он пересекает линии магнитной индукции (рис. 4.19, а, б), возникает электродвижущая сила. Свободные электроны проводника АБ движутся вместе с ним со скоростью υ. Электромагнитная сила действует на каждый электрон (силы Лоренца) и, согласно правилу левой руки, направлена вдоль проводника, а по величине определяется выражением (4.24), которое в применении к заряду электрона принимает вид Fл = В e 0υ. Под действием этой силы электроны переме-щаются к одному концу проводника, где создают избыточный отрицательный заряд, а на другом конце образуется такой же по величине положительный заряд. Разделение зарядов приводит к возникновению электрического поля в проводнике и сил притяжения заряженных частиц Fк (силы Кулона), направленных против сил Лоренца.
Рис. 4.19
Если проводник движется с постоянной скоростью, то величина сил Лоренца остается неизменной, а силы Кулона растут по мере накопления зарядов. Разделение зарядов прекращается при равенстве электромагнитных и электрических сил. Равенство сил означает наличие между концами проводника АБ установившейся разности потенциалов VA — VБ. Предположим, что шины, по которым катится проводник АБ,металлические и соединены между собой резистором R. Эти элементы вместе образуют замкнутый проводящий контур, в котором под действием разности потенциалов VA — VБпоявится электрический ток. При наличии тока заряды на концах проводника АБнейтрализуются, однако если движение его продолжается, то одновременно происходит разделение зарядов, т. е. установится непрерывный процесс, в результате которого в контуре поддерживаются постоянная электродвижущая сила Е = VA — VБ и постоянный электрический ток I. Величину э.д.с. легко найти из условия равенства сил Fл = Fк и принимая угол между направлениями магнитного поля и движения проводника α =90° В e 0υ = Отсюда следует формула для определения э.д.с. E = B υ l. (4.35) При угле α ≠ 90° в эту формулу вместо полной скорости вводится проекция ее на направление, перпендикулярное направлению магнитной индукции υ sinα, и тогда полу-чается более общая формула E = B υ l sin α (4.36) В данном случае для определения направления э.д.с. применяют правило правой руки (рис. 4.20): правую руку надо расположить так, чтобы линии магнитной индукции упирались в ладонь, а большой палец, отогнутый в плоскости ладони перпендикулярно вытянутым четырем, показывал направление движения проводника, тогда вытянутые четыре пальца показывают направление э.д.с.
 Взаимное преобразование механической и электрической энергии. Электромагнитная индукция и силовое действие магнитного поля на проводник с током используется для преобразования механической энергии в электрическую, а также электрической энергии в механическую. Такие преобразования энергии происходят в электрических машинах. Рассмотрим принципы взаимного преобразования механической и электрической энергии, используя схему на рис. 4.19. Взаимное преобразование механической и электрической энергии. Электромагнитная индукция и силовое действие магнитного поля на проводник с током используется для преобразования механической энергии в электрическую, а также электрической энергии в механическую. Такие преобразования энергии происходят в электрических машинах. Рассмотрим принципы взаимного преобразования механической и электрической энергии, используя схему на рис. 4.19.
Проводник АБ движется в магнитном поле под действием силы Fмx с постоянной скоростью υза счет механической энергии какого-либо первичного двигателя (источника механической энергии), механическая мощность которого Pмх = Fмхυ. В проводнике возбуждается э.д.с. Е и ток I = Е / (r + R), где r — сопротивление проводника, R — сопротивление внешней части цепи (шины, электроприемника). Проводник АБ в данном случае является источником э.д.с., электрическая мощность которого P = EI. С появлением тока возникает электромагнитная сила Fм, которая согласно правилу левой руки действует на проводник АБ противоположно силе Fмх (Fмх — сила движущая, Fм — сила тормозная). При постоянной скорости (установившееся движение) Fмх = Fм. Учитывая это равенство и формулы (4.24), (4.35), получим: Pмх = Fмхυ = BI l υ = ЕI = = Р. Следовательно, механическая мощность первичного двигателя равна электрической мощности источника, т. е. при движении проводника в магнитном поле под действием внешней механической силы механическая энергия полностью превращается в электрическую. Напряжение UАБ на концах проводника одновременно приложено и к внешней части цепи. Оно меньше э.д.с. на величину внутреннего падения напряжения: UАБ = Е – Ir = IR.
 Обратный процесс — преобразование электрической энергии в механическую можно показать на том же проводнике АБ, изменив несколько электрическую цепь, в которую он входит (рис. 4.21). Вместо приемника электрической энергии в цепь включен источник э.д.с. Е0, под действием которого в проводнике АБ возникает ток I. В результате взаимодействия магнитного поля и тока на проводник АБ действует электромагнитная сила Fм и он движется со скоростью υ. В проводнике АБ, движущемся в магнитном поле, индуктируется э.д.с. Е, направленная противоположно току (противо-э.д.с.). По второму закону Кирхгофа, UАБ —Е = Ir; отсюда ток Обратный процесс — преобразование электрической энергии в механическую можно показать на том же проводнике АБ, изменив несколько электрическую цепь, в которую он входит (рис. 4.21). Вместо приемника электрической энергии в цепь включен источник э.д.с. Е0, под действием которого в проводнике АБ возникает ток I. В результате взаимодействия магнитного поля и тока на проводник АБ действует электромагнитная сила Fм и он движется со скоростью υ. В проводнике АБ, движущемся в магнитном поле, индуктируется э.д.с. Е, направленная противоположно току (противо-э.д.с.). По второму закону Кирхгофа, UАБ —Е = Ir; отсюда ток
I = (UАБ – Е) / r. В данном случае, в отличие от схемы рис. 4.19, электромагнитная сила Fм движущая, а противодействие движению оказывает механическая сила Fмх (например, сила трения). При равенстве этих сил Fм = Fмх скорость движения проводника = const. Составим баланс мощностей для данной электрической цепи. Проводник АБ является электроприемником и его мощность Р = UАБI, но UАБ = Е + Ir, поэтому P = EI + I2r. С учетом выражения (4.35) P = Bυ l I + I2r. Первое слагаемое в этойсумме выражает механическую мощность движущегося проводника, а второе — мощность тепловых потерь в проводнике АБ (по закону Джоуля — Ленца).
Примеры решения задач Ë
1. В однородном магнитном поле с индукцией В = 0,04 Тл на подвесе помещен проводник длиной l = 70 см перпендикулярно линиям поля (рис.). Определить электромагнитную силу при токах I = 0,5; 1,0; 1,5; 2,0 и 2,5 А. При каком значении тока произойдет разрыв нити, если сила натяжения для ее разрыва Fн = 0,08 H, сила тяжести проводника Р = 0,018 H? Определить минимальный ток для разрыва нити подвеса.
2. На половину длины каркаса с наружным диаметром D = 240мм и внутренним - d = 190мм, имеющим прямоугольное сечение площадью S = 400мм2,равномерно нанесена обмотка медным проводом. Определить число витков, индуктивность, сопротивление обмотки и необходимую длину провода (для намотки в один ряд), если магнитная индукция катушки на ее оси составляет В = 1,6ּ10-3 Тл при токе катушки I = 3,6 А. Плотность тока J = 2 А/мм2.
3. Тогда w = 4. Определим индуктивность катушки: L = или L = 5. Найдем необходимую длину провода для намотки этой катушки. Длина одного витка l вит = 82мм. Длина провода l пр = l вит w= 82 ּ120 = 9840 мм = 9,84 м. 6. Определим диаметр и сечение медного провода, примененного для намотки катушки: Sпр = I / J = 3,6 / 2 = 1,8 мм2, dпр = 7. Тогда его сопротивление R =
Ответ: 120 витков, 21,4ּ10-6 Гн, 675 мм, 0,096 Ом.
3. Катушка, имеющая w = 500 витков, внесена в однородное магнитное поле, индукция которого возросла при этом от 0 до 0,8 Тл за время t = 0,1 с. К катушке подключен резистор сопротивлением R = 20 Ом. Определить ток и мощность, выделившуюся в резисторе, если сечение катушки S = 12 см2 и ее сопротивление Rк = 4, Ом.
4. Через центр кольца с площадью поперечного сечения S = 1 см2, средним диаметром d = 3 см и числом витков w = 100 пропущен провод. Определить ЭДС, наведенную в нем, если магнитная проницаемость сердечника μ = 3000, а ток I в обмотке кольца за t = 0,03 с изменился на 12 А.
5. На стальное кольцо с магнитной проницаемостью μ = 4000 равномерно намотаны две обмотки с числом витков w = 800 и 300. Сечение кольца круглое, площадью S = 0,8 см2, его наружный диаметр D = 50 мм. Определить энергию магнитного поля внутри кольца, если токи I = 2 А и I = 4,5 А проходят: а) в одном направлении; б) в противоположном.
4. Индуктивность L1 = 4000×1,256×10-6 5. Рассчитаем индуктивность второй катушки: L2 = 4000×1,256×10-6 6. Определим взаимную индуктивность двух катушек: М = 7. Зная L1, L2 и М, найдем значение энергии двух катушек: а) при токах, проходящих в одном направлении, W1 = б) при токах, проходящих в противоположных направлениях, W2 =
Ответ: 14,07 Дж, 0,11 Дж. Контрольные вопросы 4
1. Какие формулы из § 4.1 необходимо использовать, чтобы получить выражение (4.10) для определения индуктивности катушки? 2. Для определения собственной индуктивности служат формулы (4.9), (4.10), (4.11). После их анализа можно ли утверждать, что индуктивность не зависит от значений тока и потокосцепления? 3. Характеристика намагничивания В = f (Н) ферромагнитного материала, из которого изготовлен сердечник катушки (см. рис. 4.3, б), известна. Какие величины необходимо знать еще, чтобы построить кривую намагничивания сердечника катушки Ф = f (I)? 4. Характеристики В = f (Н) и Ф = f (I) по предыдущему вопросу предполагается построить на одном чертеже так, что ось ординат — общая для В и Ф, а ось абсцисс — общая для Н и I. Можно ли масштабы величин подобрать так, чтобы вторая кривая во всех точках чертежа совпала с первой? 5. Какое поле возникает вокруг движущихся электрических зарядов? а) магнитное; б) электрическое; в) электромагнитное. 6. Напряженность магнитного поля Н = 0,57, m = 5. Определить индукцию магнитного поля В а) В = 200 Вб; б) В = 0,25 × 10-3 Вб. 7. Какой характеристике магнитного поля соответствует размерность генри на метр (Г/м)? а) Н; б) m0 8. Какой величеной является магнитный поток Ф? а) векторной; б) скалярной. 9. Какой величиной является магнитное напряжение Uм?
б) скалярной. 10. Имеется однородное магнитное поле напряженностью Н=5А/см. Определить магнитное напряжение на пути АВ, если l АВ =10см. а) 50А; б) 0.
а) å I = 10А; б) å I = 0. 12. Влияет ли направление обхода контура на конечный результат при использовании закона полного тока? а) не влияет; б) влияет. 13. Какое свойство магнитной цепи является главным? а) нелинейная зависимость В (Н); б) способность насыщаться; в) малое магнитное сопротивление. 14. Магнитный поток, пронизывающий контур, изменяется по закону Ф = Фm sin w t По какому закону будет изменяться ЭДС? а) е = - Em sin w t б) е = const в) е = - Em cos w t 15. Укажите единицу измерения для потокосцепления в СИ: а) А м; б) Вб. Задачи для самостоятельного решения?
(Ответ: Вв = 10-3 Тл).
2. На кольцо из неферромагнитного материала (см. рис. 4.3, б), радиус которого по средней линии r= 10 см и площадь поперечного сечения S = 10 см2, равномерно уложено N = 300 витков. Определить магнитное потокосцепление катушки при токе в ней I = 30 А. Найти ток в той же обмотке, если собственное потокосцепленне Ψ = 18 · 10-4 Вб. (Ответ: Ψ = 27·10-4 Вб).
(Ответ: L = 0,3 мГн).
(Ответ: а) L = 0,098 Гн).
(Ответ: а) L = 0,133 Гн).
(Ответ: а) L = 8,64·10-4 Гн, I = 25А).
(Ответ: I = 4,5А).
(Ответ: I = 14,76А).
(Ответ: Fм = 19,2 Н [при α = 90°]).
(Ответ: FмА = 249,1 Н).
Рис. 4.26
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 871; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.188.17 (0.013 с.) |



 sinβ = IФmsinβ. В начальном положении контура магнитный поток, сцепленный с ним, равен нулю, поэтому величина магнитного потока в промежуточном положении контура является изменением потока, т. е. Фmsinβ = ΔФ, а ΔA = IΔФ.
sinβ = IФmsinβ. В начальном положении контура магнитный поток, сцепленный с ним, равен нулю, поэтому величина магнитного потока в промежуточном положении контура является изменением потока, т. е. Фmsinβ = ΔФ, а ΔA = IΔФ.

 . (4.28)
. (4.28) Рис. 4.17
Рис. 4.17

 Э.д.с. самоиндукции и взаимной индукции пропорциональны скорости изменения тока d i /dt. Коэффициентом пропорциональности является индуктивность собственная [см. формулу (4.32)] или взаимная [см. формулы (4.33) и (4.34)]. В правой части этих формул, как и в формулах (4.30), (4.31), поставлен знак «минус», что указывает на соответствие направления э.д.с. правилу Ленца: э.д.с. самоиндукции или взаимной индукции противодействует изменению тока, т. е. замедляет увеличение или уменьшение тока, причем это противодействие тем сильнее, чем быстрее изменяется ток.
Э.д.с. самоиндукции и взаимной индукции пропорциональны скорости изменения тока d i /dt. Коэффициентом пропорциональности является индуктивность собственная [см. формулу (4.32)] или взаимная [см. формулы (4.33) и (4.34)]. В правой части этих формул, как и в формулах (4.30), (4.31), поставлен знак «минус», что указывает на соответствие направления э.д.с. правилу Ленца: э.д.с. самоиндукции или взаимной индукции противодействует изменению тока, т. е. замедляет увеличение или уменьшение тока, причем это противодействие тем сильнее, чем быстрее изменяется ток.

 .
.
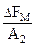 =
=  =
= 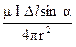
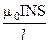
 ln
ln 






 =
=  = 215мм;
l ср = 3,14ּ215 = 675 мм.
2. Напряженность поля можно определить из соотношения
В = μμ0Н,
откуда H =
= 215мм;
l ср = 3,14ּ215 = 675 мм.
2. Напряженность поля можно определить из соотношения
В = μμ0Н,
откуда H =  =
=  = 1274 А/м.
= 1274 А/м.
 =
=  = 120 витков.
= 120 витков. =
=  =
=  = 21,4ּ10-6 Гн,
= 21,4ּ10-6 Гн, =
=  = 21,4ּ10-6 Гн.
= 21,4ּ10-6 Гн. =
=  = 0,57 мм.
= 0,57 мм. = 0,0176ּ
= 0,0176ּ  = 0,096 Ом.
= 0,096 Ом. = – 500ּ10-4
= – 500ּ10-4  = – 4,8 В.
2. Зная сопротивление всей цепи R = 24Ом, определим ток в катушке: I = U / R = 4,8 / 24 = 0,2 А.
3. Мощность, выделившаяся на резисторе,
P = I2R = (0,2)2ּ20 = 0,8 Вт.
Ответ: 0,2 А, 0,8 Вт.
= – 4,8 В.
2. Зная сопротивление всей цепи R = 24Ом, определим ток в катушке: I = U / R = 4,8 / 24 = 0,2 А.
3. Мощность, выделившаяся на резисторе,
P = I2R = (0,2)2ּ20 = 0,8 Вт.
Ответ: 0,2 А, 0,8 Вт.
 .
2. Для ее определения необходимо найти значение взаимной индуктивности:
М =
.
2. Для ее определения необходимо найти значение взаимной индуктивности:
М =  =
=  =
=  = =0,4ּ10-3 Гн.
3. Тогда е = - 0,4ּ10-3ּ
= =0,4ּ10-3 Гн.
3. Тогда е = - 0,4ּ10-3ּ  = 0,16 В = 160 мВ.
Ответ: 0,2 А, 0,8 Вт.
= 0,16 В = 160 мВ.
Ответ: 0,2 А, 0,8 Вт.
 +
+  = ± MI1I2.
2. Прежде чем определить эту энергию, найдем L1, L2 и М. Найдем индуктивность первой катушки:
L1 =
= ± MI1I2.
2. Прежде чем определить эту энергию, найдем L1, L2 и М. Найдем индуктивность первой катушки:
L1 =  ,
где l ср = pDср; (Dср = D – d).
3. Найдем диаметр поперечного сечения кольца d из выражения S = pd2 / 4:
d =
,
где l ср = pDср; (Dср = D – d).
3. Найдем диаметр поперечного сечения кольца d из выражения S = pd2 / 4:
d =  =
=  = 10,4 мм
и Dср = 50 – 10,4 = 39,6 мм.
= 10,4 мм
и Dср = 50 – 10,4 = 39,6 мм.
 = 2,06 Гн.
= 2,06 Гн. = 0,29 Гн.
= 0,29 Гн. = 4000×1,256×10-6×300
= 4000×1,256×10-6×300  = 0,775 Гн.
= 0,775 Гн. +
+  + 0,775 × 2× 4,5 = 14,07 Дж;
+ 0,775 × 2× 4,5 = 14,07 Дж; а) векторной;
а) векторной; 11. Заданы токи: I1 =2А, I2 = 3А. Определить полный ток, пронизывающий поверхность S.
11. Заданы токи: I1 =2А, I2 = 3А. Определить полный ток, пронизывающий поверхность S.
 В проводах воздушной линии, расположенных на одинаковом расстоянии l = 10 см друг от друга(рис. 4.26), токи IВ = IС = 6000 А направлены в одну сторону, а ток IА = 12 000 А противоположно. Определить силу, действующую на 1 м каждого провода.
В проводах воздушной линии, расположенных на одинаковом расстоянии l = 10 см друг от друга(рис. 4.26), токи IВ = IС = 6000 А направлены в одну сторону, а ток IА = 12 000 А противоположно. Определить силу, действующую на 1 м каждого провода. Магнитный поток в сердечнике катушки, создаваемый током в ее обмотке, изменяется по графику рис. 4.27. П
Магнитный поток в сердечнике катушки, создаваемый током в ее обмотке, изменяется по графику рис. 4.27. П 


