
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрическая емкость. КонденсаторыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
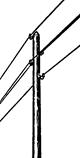
Электрическая емкость проводника и между проводниками. Электрическая емкость проводника — величина, характеризующая способность проводника накапливать электрический заряд, численно равная отношению заряда проводника к его потенциалу: С = Q / V, (2.7) где С – электрическая емкость, Ф (фарад). В системе заряженных проводников на заряд и потенциал каждого из них влияют форма, расположение и величины зарядов других проводников. В этом случае применяют понятие емкости между проводниками. Наибольшее значение для практики имеют системы из двух проводников, имеющих равные по величине, но противоположные по знаку заряды. Примерами таких систем являются два провода воздушной линии электросети (рис. 2.7), две жилы электрического кабеля, жила кабеля и его броня (рис. 2.8), токоведущий стержень и кожух проходного изолятора, два электрода электронной лампы и т. д.
Рис. 2.7 Рис. 2.8 Силовой кабель
Электрическая емкость между двумя проводниками — величина, равная отношению электрического заряда (Q) одного проводника к разности потенциалов (U) между этими проводниками: C = Q / (V1 - V2) = Q / U.(2.8) Электрические конденсаторы. Электрическая емкость между проводниками определяется конструкцией электрических устройств и ее приходится учитывать при расчетах, монтаже и эксплуатации электрических и особенно радиотехнических устройств. Однако в электротехнике, радиотехнике, электронике широко применяют устройства с электрической емкостью, специально построенные и предназначенные для создания электрического поля и хранения его энергии. Элемент электрической цепи, предназначенный для использования его электрической емкости, называется электрическим конденсатором. Электрические конденсаторы входят в схемы колебательных контуров, усилителей напряжения и мощности, электрических фильтров и других элементов и узлов радиотехнической и электронной аппаратуры. В электрических сетях переменного тока конденсаторы применяют для компенсации реактивной мощности. Электрический конденсатор имеет два проводника (их иногда называют обкладками), которые разделены диэлектриком, по форме проводников различают конденсаторы плоские (рис. 2.9, а), цилиндрические (рис. 2.9, б).
а) б) Рис. 2.9
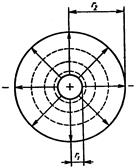
Для определения емкости плоского конденсатора воспользуемся формулой (2.5) и формулой Е = s / e0 (табл. 2.1), заменив в ней электрическую постоянную e0 диэлектрической проницаемостью диэлектрика e а: Е = s / eа; U / d = s / eа, где d — расстояние между обкладками конденсатора. Умножим обе части равенства на S (S – площадь одной обкладки), получим выражение емкости плоского конденсатора C = Q / U = eа S / d. (2.9) Емкость цилиндрического конденсатора выражает формула (2.10), а двухпроводной воздушной линии (рис. 2.10) — формула (2.11):
где l — длина цилиндрического конденсатора или участка линии;
здесь r1; r2 — радиусы обкладок внутренней и внешней; а — расстояние между осями проводов линии; r0 — радиус провода. Диэлектрики, применяемые для изготовления конденсаторов, в большинстве случаев имеют постоянную величину диэлектрической проницаемости, независимую от напряженности электрического поля. Поэтому конденсаторы имеют постоянную величину емкости.
Рис. 2.10 Рис. 2.11
У сегнетоэлектриков eа зависит от напряженности электрического поля, поэтому конденсаторы с сегнетоэлектриками (вариконды) имеют нелинейную вольт-кулонову характеристику q = f (U). Их применяют в автоматике и радиотехнике в схемах диэлектрических усилителей постоянного и переменного токов, умножителей и делителей частоты, стабилизаторов напряжения и т. д. В зависимости от назначения, рабочих характеристик (величин емкости, напряжения, частоты) промышленность выпускает конденсаторы, отличающиеся по конструкции и материалам: бумажные, электролитические и др. В бумажном конденсаторе проводники — две длинные ленты алюминиевой фольги изолированы лентами парафинированной бумаги (рис. 2.11). Одной из обкладок электролитического конденсатора также служит алюминиевая фольга 2, другая обкладка из бумаги или ткани 1, пропитанной электролитом. Изоляцией является тонкий слой окиси на поверхности обкладки из алюминиевой фольги. Электролитические конденсаторы работают при неизменной полярности обкладок (в цепях постоянного тока). Соединение конденсаторов. В практике иногда необходимо соединять конденсаторы в батареи, для чего применяют схемы последовательного, параллельного и смешанного соединений.
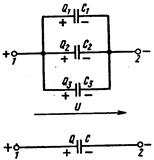
Каждый конденсатор имеет два наружных зажима (начало «Н», конец «К») для присоединения его к другим элементам. В схеме (рис. 2.12) начало следующего конденсатора соединено с концом предыдущего (последовательное соединение).
Рис. 2.12 Рис. 2.13
Источник присоединен к обкладкам крайних конденсаторов, а внутренние конденсаторы с источником непосредственно не соединены и заряжаются путем электростатической индукции. Поэтому заряд всей группы конденсаторов и каждого конденсатора один и тот же: Q = Q1 = Q2 = Q3
Для упрощения схемы и расчетов группу конденсаторов можно заменить одним конденсатором эквивалентной емкости С. Общее напряжение U в данном случае распределяется между конденсаторами обратно пропорционально их емкости [см. формулу (2.8)] и равно сумме напряжений на этих конденсаторах: U= U1 + U2 + U3. Подставим в это равенство выражения напряжений по формуле (2.8) и после сокращения на Q получим выражение для определения эквивалентной емкости
1 / С = 1 / С1 + 1 / С2 + 1 / Сз. (2.12)
В схеме (рис. 2.13) конденсаторы группы присоединены одной обкладкой в общей точке 1, а другой — в общей точке 2. К этим точкам подводится напряжение источника. При таком (параллельном) соединении группу конденсаторов тоже можно заменить одним с эквивалентной емкостью С. В данной схеме все конденсаторы группы имеют между обкладками одно и то же напряжение U, а заряды получают разные, пропорциональнои х емкости [см. формулу (2.8)]. Каждый конденсатор получает заряд независимо от других, поэтому общий заряд равен сумме зарядов отдельных конденсаторов: Q = Q1+ Q2 + Q3
Подставив сюда выражения зарядов по формуле (2.8) и сократив на U, получим формулу для определения эквивалентной емкости С = С1 + С2 + Сз. (2.13)
В схемах (рис. 2.14, а, 2.15) имеются участки с последовательным и параллельным соединением конденсаторов (смешанное соединение). Подобную группу конденсаторов можно заменить эквивалентным конденсатором с емкостью С (рис. 2.14, б, в).
а) б) в)
Рис. 2.14 Рис. 2.15
Энергия электрического поля. Электрическое поле обладает энергией, которая накапливается при образовании заряда в электрическом устройстве. Наглядным примером такого устройства является электрический конденсатор, который рассмотрим в схеме его зарядки от источника электрической энергии с постоянным напряжением U через резистор с сопротивлением R (рис. 2.16, а). Заряд конденсатора образуется переносом заряженных частиц с одной обкладки на другую под действием внешнего источника энергии. При этом одна часть энергии источника расходуется на образование заряда и запасается в виде энергии электрического поля в конденсаторе, а другая преобразуется в теплоту в резисторе и соединительных проводах.
а) б) Рис. 2.16
Работа, совершенная при переносе единицы заряда, численно равна напряжению между обкладками Us. Если бы это напряжение в процессе зарядки не изменялось, то энергию можно было бы определить произведением напряжения и заряда [см. формулу (2.4)]. Однако в процессе накопления заряда растет и напряжение, поэтому при определении энергии, затраченной на образование заряда, нужно учесть зависимость между напряжением и зарядом, которая при постоянной величине емкости конденсатора С графически выражается прямой линией (рис. 2.16, б).
Предположим, что заряд Q1 увеличился на dQ — величину столь малую, что в пределах его изменения напряжение можно считать неизменным: Us = Us1 (d Us → 0). В этом случае работа, выполненная при увеличении заряда на dQ, определяется произведением dWэ = Us1 dQ. На рис. 2.16, б работа показана заштрихованным элементом площади. Всю работу, затраченную на образование заряда, можно определить, суммируя элементы площади в пределах изменения заряда от 0 до Q и напряжения от 0 до Uc = U, т. е. площадью прямоугольного треугольника: Wэ = U Q / 2. Учитывая также формулу (2.7), получим еще два выражения для энергии электрического поля конденсатора:
W э = U Q / 2 = C U2 / 2 = Q2 / 2 C. (2.14)
Примеры решения задач Ë
1. На заряд Q = 16ּ10 –8 Кл действует сила F = 2,4ּ10 –3 Н. Найти напряженность электрического поля в данной точке. Определить заряд Q0, создающей это поле, если он удален от этой точки на расстояние r = 0,3 м в вакууме.
2. Два разнополярных заряда в стекле Q1 = + 3,5ּ10 -9 Кл и Q2 = -3,5ּ10-9 Кл находятся на расстоянии r = l8 cм друг от друга. Заряд Q3 = + 2ּ10-8 Кл расположен на расстоянии r = 24 смот этих двух зарядов. Определить значение и направление напряженности поля Е в точке, находящейся посередине между зарядами Q1 и Q2.
3. Найдем напряженность Е3: Е3 = 4. Определим вектор напряженности поля в указанной точке: Е = Е 1 + Е 2 + Е 3. Векторы Е 1 и Е 2 направлены в одну сторону (так как заряды Q1 и Q2 разноименные и Е 12 = Е 1 + Е 2= 550 + 550 = 1100 В/м. Вектор Е 3 направлен перпендикулярно вектору Е 12, и суммарный вектор напряженности: E = При определении направления вектора Е необходимо помнить, что оно совпадает с направлением силы, действующей на положительный заряд.
Ответ: 1220 В/м.
3. К выводам плоского воздушного конденсатора приложено напряжение U = 800 В. Определить напряженность электрического поля конденсатора при расстоянии между пластинами d = 5 мм и силу, действующую в этом поле на единичный заряд Q = 1,5ּ10-7 Кл. Определить емкость конденсатора, если площадь каждой пластины S = 24 см2. Как изменится его емкость, если конденсатор поместить в спирт?
Если конденсатор помещен в спирт, диэлектрическая проницаемость которого ε = 33, емкость увеличивается в 33 раза при неизменных расстоянии между пластинами и площади пластин: С' = С ε = 4,25пФ ּ33 = 140пФ.
Ответ: 140 пФ.
4. Два плоских конденсатора емкостями С1 = 0,5 мкФ и С2 = 1,5 мкФ соединены последовательно и подключены к источнику питания. При этом на обкладках конденсаторов появился заряд Q = 4,5ּ10-4 Кл. Оба конденсатора имеют одинаковые площади пластин и одинаковый диэлектрик. Определить общую (эквивалентную) емкость соединения, подведенное напряжение, падение напряжения на обоих конденсаторах и расстояние между пластинами первого конденсатора, если напряженность электрического поля второго конденсатора Е = 2000 В/см. Определить энергию электрического поля эквивалентного конденсатора.
4. Определим расстояние между пластинами второго конденсатора по (1.9): d2 = U2 / E =300 / 2000 = 0,15 см. 5. Если конденсаторы имеют одинаковые площади пластин и один и тот же диэлектрик, то С1 / С2 = d2 / d1, откуда d1 = 6. Энергию электрического поля найдем по (1.12) W = CU2 / 2 = 0,375ּ10-6ּ12002 / 2 = 0,29 Дж.
Ответ: 0,375 мкФ, 1200В, 0,45см, 0,29 Дж.
Контрольные вопросы 4
а) в области А; б) в области В?
2. Какое из приведённых утверждений вы считаете правильным? а) поле и силовые линии существуют реально; б) поле существует реально, а силовые линии условно; в) поле и силовые линии существуют условно.
3. Какой величиной является потенциал электрического поля? а) векторной;
4. Какого соотношение между потенциалами точек А и В? а) VA = VB; б) VA ¹ VB.
5. При параллельном соединении трёх конденсаторов, подключенных к источнику питания, один из них (С3) оказался пробитым. Как изменится напряжение на конденсаторах и какой станет их общая ёмкость? а) U = const; Собщ = С1 +С2; б) U = 0; Собщ = ¥.
6. Три конденсатора подключенные к источнику питания, соединены последовательно. Как будет распределяться напряжение на конденсаторах? а) U1 > U2 > U3; б) U3 > U2 > U1; в) недостаточно данных для ответа на вопрос.
7.Три конденсатора можно соединить последовательно, параллельно и по схемам смешанного соединения. Сколько схем соединения можно построить из трех конденсаторов одинаковой емкости С и какая из них имеет наименьшую эквивалентную емкость?
Задачи для самостоятельного решения?
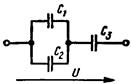
1. Два заряда Q1 = 5ּ10-8 Кл и Q2 = 12ּ10-8 Кл, находящиеся на расстоянии r = 20 см друг от друга, разделены диэлектриком, в качестве которого использована парафинированная бумага. Определить силу взаимодействия этих зарядов. Как она изменится, если убрать диэлектрик? 2. Определить силу взаимодействия двух зарядов Q = 3,5ּ10-7 Кл и Q2 = 6ּ10-7 Кл, находящихся на расстоянии r = 5 см друг от друга и помещенных в воду. 3. Два заряда Q1 и Q2, находящиеся на расстоянии r = 10 см в воздухе, взаимодействуют с силой F = 1,2 H. Определить заряд Q2, если известно, что Q1 = 6ּ10-7 Кл. 4. Между двумя зарядами Q1 = 22ּ10-7 Кл и Q2 = 5ּ10-7 Кл помещен электрокартон. Сила взаимодействия этих зарядов F = 0,8 H. Определить расстояние между ними. 5. Два заряда Q1 и Q2, находящиеся на расстоянии r = 25 см в воздухе, взаимодействуют с силой F = 0,l H. Определить заряд Q2, если Q = l,5ּ10-6 Кл. 6. Сила взаимодействия двух зарядов, находящихся в воздухе, F = 3 Н; Q1 = 3ּ10-5 Кл и Q2 = 0,6ּ10-5 Кл. Определить расстояние между ними. 7. Определить напряженность электрического поля, действующего с силой F = 5,4ּ10-4 Н на заряд Q = 1,8ּ10-3 Кл. 8. Электрическое поле с напряженностью Е = 0,8 В/м действует на заряд с силой F = 9,6ּ10-4 Н. Определить этот заряд. 9. Определить силу, с которой действует электрическое поле, имеющее напряженность Е = 1,4 В/м, на заряд Q = 4ּ10-6 Кл. 10. На расстоянии r = 1,5 см от заряда Q, находящегося в воздухе, напряженность электрического поля Е = 650 кВ/м. Определить заряд Q. 11. Определить заряд, перемещенный в точку поля с потенциалом φ = 10В, если при этом совершена работа А = 0,5ּ10-6 Дж. 12. Потенциал электрического поля φ = 20 В. Определить работу, совершаемую силами этого поля, при внесении в него заряда Q = 5,5ּ10-4 Кл. 13. Напряженность электрического поля Е = 5ּ10-2 В/м. Определить силу, с которой действует это поле на заряд Q = 1,6ּ10-3 Кл, и работу по перемещению этого заряда в точку поля с потенциалом φ = 45 В. 14. Определить разность потенциалов между двумя точками электрического поля, если при перемещении заряда Q = 0,5ּ10-6 Кл совершена работа А = 18ּ10-5 Дж. 15. Определить емкость конденсатора, если он был заряжен до напряжения U = 250 В. При этом заряд конденсатора Q = l0-4 Кл. 16. Определить напряженность электрического поля между пластинами плоского конденсатора, находящимися на расстоянии d = 3 мм, если напряжение, приложенное к ним, U = 450 В. Определить емкость этого конденсатора при условии, что заряд на его пластинах Q = 3ּ10-4 Kл. 17. Плоский воздушный конденсатор емкостью С = 1мкФ заряжен от источника постоянного тока напряжением 27 В. Определить заряд и напряженность электричес-кого поля заряженного конденсатора при расстоянии между его пластинами d = 1,5 мм. Определить также энергию электрического поля. 18. Емкость конденсатора С = 1,5 мкФ, заряд на его обкладках Q = 45ּ10-5 Кл. Определить напряжение на зажимах конденсатора. 19. Конденсатор заряжен от источника питания напряжением U = 100 В. Энергия электрического поля конденсатора W = 6·10-3 Дж. Определить его емкость. 20. К конденсатору емкостью С = 0,25 мкФ подведено напряжение U = 400 В. Определить энергию электрического поля конденсатора. 21. Определить эквивалентную (общую) емкость С двух последовательно включенных конденсаторов С1 = С2 = 0,7 мкФ. 22. Общая емкость двух последовательно включенных конденсаторов С = 1,2 мкФ. Емкость одного конденсатора С1 = 3 мкФ. Определить емкость второго конденсатора. 23. Конденсаторы емкостями С1 = 10 мкФ и С2 = 15 мкФ соединены последовательно. Определить их эквивалентную емкость. 24. Три конденсатора одинаковой емкости С1 = С2 = СЗ = 12 мкФ соединены последо-вательно. Определить их эквивалентную емкость. 25. Общая емкость трех последовательно соединенных конденсаторов С = 0,08 мкФ. Определить емкость одного из конденсаторов, если емкости С1 = 0,2 мкФ, С2 = 0,4 мкФ. Определить их эквивалентную емкость при параллельном соединении конденсаторов. 26. Четыре конденсатора емкостями С7 = 0,18 мкФ, С2 = 0,7 мкФ, C3 = 0,12 мкФ и С4 = 0,5 мкФ соединены параллельно. Определить их эквивалентную емкость. 27. Три конденсатора емкостями С1 = 47 пФ, С2 = 18 пФ, С3 = 75 пФ соединены параллельно, и к ним последовательно подключен конденсатор С4 = 75 пФ. Определить общую емкость цепи и эквивалентную емкость конденсаторов, если конденсатор С4 подсоединить параллельно. 28. На рис. представлена схема соединения конденсаторов, где С1 = С2 = 1 мкФ, С3 = 2 мкФ. Определить эквивалентную емкость.
29. Общая емкость двух последовательно соединенных конденсаторов Соб = 18 мкФ. Определить емкость каждого конденсатора, если напряжение на зажимах цепи U = 450 В, а на конденсаторе С1 U1 = 150 В. 3. Электрические цепи постоянного тока 3.1 Понятие об электрической цепи и её элементах. Условные обозначения на схемах ……………………………………………….. 33 3.2 Основы расчета электрических цепей постоянного тока ……………………… 35 3.3 Режимы работы электрических цепей …………………………………………... 36 3.4 Характерные особенности последовательного соединения резисторов и источников ……………………………………………………………………… 36 3.5 Характерные особенности параллельного соединения резисторов и источников ………………………………………………………………………. 37 3.6 Метод свёртывания схем. Смешанное соединение источников электрической энергии …………………………………………………………… 38 3.7 Первый закон Кирхгофа …………………………………………………………. 38 3.8 Второй закон Кирхгофа ………………………………………………………….. 38 3.9 Плавкие предохранители ………………………………………………………… 39 3.10 Выбор сечения проводов по условиям нагрева и потери напряжения ………... 39 Основные формулы ……………………………………………………….... 41 Обозначения ……………………………………………………………….... 42 Примеры решения задач ……………………………………………………. 43 Контрольные вопросы ……………………………………………………....45 Задачи для самостоятельного решения …………………………………….45
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 656; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.132.80 (0.014 с.) |




 , (2.10)
, (2.10)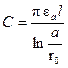 (2.11)
(2.11)



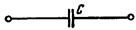



 ;
2. Напряженность электрического поля: Е = Fэ / Q2 или Е = Q / (4pe0 r2).
3. Работа: А1.2 = Е Q l.
4. Электрическое напряжение: U = A1.2 /Q или U = Е l; U1.2 = V1 – V2.
5. Потенциал поля в точке 1,2: V1 = А1 /Q; V2 = А2 / Q;
6. Электроёмкость проводника: С = Q / V,
между двумя проводниками: C = Q / (V1 - V2) = Q / U
7. Ёмкость плоского конденсатора: C = Q / U = e а S / d
8. Ёмкость цилиндрического конденсатора:
;
2. Напряженность электрического поля: Е = Fэ / Q2 или Е = Q / (4pe0 r2).
3. Работа: А1.2 = Е Q l.
4. Электрическое напряжение: U = A1.2 /Q или U = Е l; U1.2 = V1 – V2.
5. Потенциал поля в точке 1,2: V1 = А1 /Q; V2 = А2 / Q;
6. Электроёмкость проводника: С = Q / V,
между двумя проводниками: C = Q / (V1 - V2) = Q / U
7. Ёмкость плоского конденсатора: C = Q / U = e а S / d
8. Ёмкость цилиндрического конденсатора: 




 = 550 В/м.
2. Напряженность Е2 = 550 В/м, так как Q1 = Q2 и r1 = r1.
Для определения напряженности в этой же точке от действия заряда Q3 необходимо найти расстояние r3 этой точки от заряда Q3: из прямоугольного треугольника имеем
r3 =
= 550 В/м.
2. Напряженность Е2 = 550 В/м, так как Q1 = Q2 и r1 = r1.
Для определения напряженности в этой же точке от действия заряда Q3 необходимо найти расстояние r3 этой точки от заряда Q3: из прямоугольного треугольника имеем
r3 = 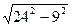 = 22,2 см.
= 22,2 см.
 = 520 В/м.
= 520 В/м.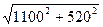 = 1220 В/м.
= 1220 В/м. = 4,25ּ10-12 Ф = 4,25 пФ.
= 4,25ּ10-12 Ф = 4,25 пФ.
 = 0,45 см.
= 0,45 см. 1. На рисунке показана модель атома водорода. В какой области пространства действует электрическое поле
1. На рисунке показана модель атома водорода. В какой области пространства действует электрическое поле б) скалярной.
б) скалярной.



