
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электроёмкость. Конденсаторы..Содержание книги Поиск на нашем сайте
Рассмотрим проводник, находящийся в однородной среде вдали от заряжённых тел и других проводников. Такой проводник назовём уединённым. Сообщим такому проводнику некоторый заряд q. Этот заряд распределится по поверхности так, чтобы напряжённость поля внутри проводника равнялась нулю. А все точки внутри проводника и на поверхности приобретут некоторый одинаковый потенциал φ. Поместим теперь на тот же проводник заряд q`=n*q, т.е в n раз больший. Чтобы поле внутри проводника вновь равнялось 0, заряд q` должен распределиться по поверхности проводника подобно заряду q. Очевидно, что и потенциал проводника увеличиться в n раз. Т.е. потенциал в каждой точке поля прямо пропорционален заряду проводника. Будем сообщать проводнику разные по величине заряды q’,q’’,q’’’ и т.д. Соответственно потенциал проводника будет приобретать значения φ’, φ’’, φ’’’.. Однако отношение заряда к потенциалу будет оставаться постоянным для данного проводника.
Следовательно, это отношение может служить характеристикой самого проводника. Отношение q к
Из (1) можно написать:
Электроёмкость уединённого проводника численно равна величине заряда, который нужно сообщить данному проводнику для увеличения его потенциала на единицу. В СИ за единицу электроёмкости принимают ёмкость такого проводника, при сообщении которому заряда в 1Кл его потенциал изменяется на 1В. Эта единица называется фарадой.
1Ф=1Кл/1В
Вычислим электроёмкость уединённого сферического проводника. Потенциал шара радиуса R на котором находится заряд q равен:
В СИ коэффициент k равен 9*109 м/ф. Из (2) следует, что электроёмкостью равной 1 фараде, обладает проводящий шар находящийся в вакууме (
Это примерно в 1500 раз больше радиуса Земли. Т.о. фарада- очень большая величина, поэтому на практике пользуются единицами равными долям фарады 1 мкф=10-6ф 1 пф=10-12ф
Конденсаторы.
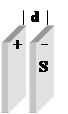
Мы рассмотрели электроёмкость уединённого проводника. Рассмотрим теперь, как влияют на электроёмкость проводника другие окружающие его тела (проводники или диэлектрики). Под действием поля, создаваемого заряженным проводником А, на окружающих телах возникают индуцированные заряды (на проводниках) или связанные заряды (на диэлектриках). Заряды, противоположные по знаку заряду проводника А, располагаются ближе к проводнику, чем одноимённые и следовательно оказывают большее влияние на его потенциал и, следовательно, потенциал проводника уменьшается по абсолютной величине. Согласно формуле Конденсаторы делают в виде двух проводников (обкладок), расположенных близко к друг другу. Чтобы внешние тела не оказывали воздействия на ёмкость конденсатора, обкладкам придают такую форму и так располагают их друг относительно друга, чтобы поле было полностью сосредоточено внутри конденсатора. Этому условию удовлетворяют две параллельных пластинки, два коаксиальных цилиндра, две концентрические сферы расположенные близко друг к другу. Соответственно бывают плоские, цилиндрические и сферические конденсаторы. Поскольку поле заключено внутри конденсатора, заряды на обкладках должны быть равны по величине и противоположны по знаку. Под ёмкостью конденсатора понимается физическая величина, равная отношению заряда одной из обкладок q к разности потенциалов
Величина емкости конденсатора зависит от формы и размера обкладок и расстояния между ними, а также от диэлектрических свойств среды, заполняющей пространство между обкладками. Найдём формулу для ёмкости плоского конденсатора. Пусть заряд на обкладках q, площадь обкладки S и расстояние между обкладками d.
Рассмотрим сферический конденсатор. Поле между обкладками создаётся только зарядом на внутренней сферической обкладке
Из (1) и (2) видно, что С~
Энергия электрического поля
Зарядить некоторый проводник означает перенести на его поверхность из бесконечности некоторый заряд q. Перенос первой порции заряда Пусть имеется проводник, у которого емкость, заряд и потенциал соответственно равны С, q,
Так как. потенциал в процессе зарядки меняется, то выражение (1) может быть записано только для элементарной работы. Полная работа по зарядке тела от нулевого потенциала до потенциала
Очевидно, что энергия заряженного тела равна той работе, которую надо совершить, чтобы зарядить это тело
Используя связь между c,
Выражение (3) представляет собой собственную энергию заряженного тела.
Если мы имеем систему заряженных тел, то, поскольку W есть скалярная величина, полная энергия системы будет равна сумме энергий отдельно заряженных тел.
Конденсатор можно представить как систему зарядов: заряд +q находится в точках с потенциалом
Увеличение потенциала
где V=Sd- объем электростатического поля между обкладками конденсатора, что и требовалось доказать. Поле в конденсаторе однородное и следовательно заключенная в нем энергия распределяется в пространстве с одинаковой плотностью w Следовательно, плотность энергии поля конденсатора равна:
Исследования неоднородных электрических полей, создаваемых произвольными заряженными телами, показали, что для них формула (6) неприменима, тогда как выражение (7) остается справедливым и определяет объемную плотность энергии в каждой точке любого электрического поля. Поэтому, энергия dW бесконечно малого объема dV поля равна
Полная энергия поля равна
Диэлектрики в электрическом поле
В нескольких последующих параграфах мы рассмотрим электрические свойства непроводящих веществ – диэлектриков. Диэлектрики отличаются от металлов тем, что в них нет свободных электрических зарядов, способных под действием электрического поля перемещаться через весь диэлектрик.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 668; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.151.211 (0.007 с.) |


 есть постоянная для данного проводника величина и называется электроёмкостью или просто ёмкостью С проводника.
есть постоянная для данного проводника величина и называется электроёмкостью или просто ёмкостью С проводника. (1)
(1)

 и имеющий радиус
и имеющий радиус
 между обкладками.
между обкладками.
 Тогда
Тогда 
 - диэлектрическая проницаемость вещества между обкладками конденсатора.
- диэлектрическая проницаемость вещества между обкладками конденсатора.

 не сопровождается совершением работы. Для переноса же каждой последующей порции заряда
не сопровождается совершением работы. Для переноса же каждой последующей порции заряда  (1)
(1)
 (2)
(2)


 - (3)
- (3) (4)
(4) , а заряд
, а заряд  -q в точках с потенциалом
-q в точках с потенциалом  . Тогда по формуле (4) энергия заряженного конденсатора равна
. Тогда по формуле (4) энергия заряженного конденсатора равна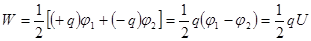 или
или (5)
(5) ;
;  ;
; 


 (6)
(6)


 (8)
(8) (9)
(9)


