
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные свойства и характеристики магнитного поля.Содержание книги
Поиск на нашем сайте
Магнитное поле обнаруживается в пространстве, окружающем движущиеся заряженные частицы, с которыми это поле связано. В проводнике и пространстве вокруг него магнитное поле обусловлено этим током, а внутри и вокруг намагниченного тела — внутриатомным и внутримолекулярным движением заряженных частиц (например, вращением электронов вокруг своих осей и вокруг ядра атома). Главным свойством магнитного поля является силовое действие на движущуюся электрически заряженную частицу, причем сила воздействия пропорциональна заряду частицы и ее скорости. Это свойство магнитного поля положено в основу для определения его количественных характеристик, без которых невозможны изучение магнитных явлений и расчеты, связанные с их практическим использованием.
Величина, численно равная произведению тока проводимости (I) вдоль линейного проводника и бесконечно малого отрезка этого проводника (Δ l): А = I Δ l называется элементом тока. Сила взаимодействия двух элементов тока прямо пропорциональна произведению этих элементов тока и обратно пропорциональна квадрату расстояния между ними: Δ Fм =
А – элемент тока, Аּм; r – расстояние между элементами тока; α – угол между направлениями А1 и r; μ0 = 4π ּl0-7 Предположим, что источником магнитного поля является провод с током I1, а ток I2 настолько мал, что не изменяет характеристик этого поля. В данном случае элемент тока А2 является пробным, с помощью которого можно обнаружить силу Fм и исследовать магнитное поле в различных точках пространства. Каждый из двух элементов тока (A1 и А2) создает свое магнитное поле; в окружающем их пространстве одно поле накладывается на другое и образуется общее магнитное поле (принцип наложения полей). Силовое взаимодействие двух токов следует рассматривать как результат действия на каждый из них общего магнитного поля, созданного этими токами. Магнитная индукция. Важные для практики свойства и характеристики магнитного поля зависят от формы проводника, значения и направления тока в нем, от взаимного расположения проводников (если поле создается группой проводников), свойств среды и т. д. Поэтому магнитные поля, созданные при различных условиях, отличаются одно от другого по форме и количественным показателям.
Для того чтобы сопоставлять магнитные поля, оценивать возможности их использования и вести соответствующие расчеты, установлены и применяются их силовые и энергетические характеристики. Из выражения (4.1) видно, что сила Fм зависит от величины пробного элемента тока А2, поэтому в качестве характеристик магнитного поля служить не может. Силовой характеристикой магнитного поля является вектор магнитной индукции В. Магнитная индукция — векторная величина, численно равная отношению силы, действующей на заряженную частицу к произведению заряда и скорости частицы, если направление скорости таково, что эта сила максимальна.
Рис. 4.2
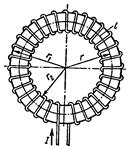
Направление магнитной индукции перпендикулярно векторам силы На основе этого определения получим выражение элементарной магнитной индукции: ΔВ = Из формулы(4.1) следует ΔВ = отсюда ΔВ = где ΔВ — магнитная индукция, Тл (тесла); I Δ l — пробный элемент тока, А·м. Формула (4.2) выражает закон Био–Савара и определяет элементарную магнитную индукцию в любой точке С пространства на расстоянии r от оси провода с током. Провод конечных размеров состоит из множества элементов, поэтому магнитную индукцию в заданной точке можно найти как векторную сумму элементарных величин ΔВ, взятую по всей длине провода. Для длинного прямого провода с током I (рис. 4.2, а) такое решение приводит к формуле В = µ0I/2πr, а магнитная индукция в центре кольцевого витка провода с током I (рис. 4.2, б) В =µ0I / 2 rк, где rк — радиус кольцевого витка. Внутри катушки (рис. 4.3, а) длиной l, имеющей N витков при токе в них I, магнитная индукция B = µ0I N / l. (4.3)
a) б) Рис. 4.3 Для катушки с кольцевым неферромагнитным сердечником (рис. 4.3, б) l = 2πr, где r – радиус сердечника. Наглядное изображение магнитного поля выполняют с помощью линий магнитной индукции (силовых линий). В каждой точке такой линии направление вектора магнитной индукции совпадает с касательной к этой линии (рис. 4.2, а, 4.3, a).
Из формулы (4.3) и рис. 4.3, а видно, что магнитная индукция внутри длинной цилиндрической катушки одинакова по величине и направлению во всех точках. Такое магнитное поле называю однородным (или равномерным). Магнитный поток и потокосцепление. На рис. 4.3, а перпендикулярно оси катушки расположена плоскость S (след ее показан штрих-пунктирной линией). В данном случае линиимагнитной индукции равномерного поля пронизывают эту плоскость под прямым углом (между направлением линий магнитной индукции и нормалью к поверхности S угол α = 0). В качестве характеристики магнитного поля катушки, кроме величины магнитной индукции, определяют потокмагнитнойиндукции (магнитный поток), который при заданных условий (В = const, α = 0°) выражается произведением Ф = В S, (4.4) где Ф — магнитный поток, Вб (вебер). Предположим, что число линий магнитной индукции, приходящееся на единицу площади (плотность линий), численно равно величине магнитной индукции В. Тогда общее число линий внутри катушки составляет BS (S — площадь поперечного сечения катушки или площадь, ограниченная витком), т. е. численно равно потоку магнитной индукции катушки. Если линии магнитной индукции пронизывают поверхность при α ≠ 0, то магнитный поток определяют по формуле Ф = ВS соs α. (4.5) Подставим в формулу (4.4) выражение магнитной индукции (4.3), получим Ф = В магнитном поле катушки рис. 4.3, б рассмотрим некоторый замкнутый контур l, сцепленный с ее N витками. Полный ток, охватываемый этим контуром, выражается произведением IN. От значения полного тока прямо пропорционально зависит магнитный поток катушки [см. формулу (4.6)], поэтому величину IN называют также намагничивающей силой F = IN, (4.7) где F — намагничивающая сила, А. Направление намагничивающей силы связано с направлением тока в витках катушки и его можно определить по правилу буравчика: если ручку правоходового буравчика вращать по направлению тока в витках, то поступательное движение буравчика покажет направление намагничивающей силы катушки с током (рис. 4.3, а). Рис. 4.3, а дает наглядное представление о том, что линии магнитной индукции окружены витками катушки и замыкаются, охватывая витки. Говорят, что магнитный поток сцеплен с витками катушки, а для расчетов введена величина потокосцепления. Сумма магнитных потоков, сцепленных с отдельными витками катушки, называется потокосцеплением. Потокосцепление катушки, все N витков которой сцеплены с магнитным потоком Ф, выражается произведением Ψ = ФN, (4.8) где Ψ — потокосцепление, Вб. Потокосцепление катушки называют собственным или потокосцеплением самоиндукции, если оно обусловлено током этой катушки. На рис. 4.4, а, б потокосцепление катушки N1 собственное Ψ1.1 = Ф1N1. Потокосцепление некоторой катушки, обусловленное электрическим током другой катушки, называют взаимным или потокосцеплением взаимной индукции.
а) б) Рис. 4.4
Катушка N2 на рис. 4.4, а, б имеет взаимное потокосцепление Ψ1.2 = Ф1.2N2, причем на рис.4.4, а Ф1.2 = Ф1, а на рис.4.4, б Ф1.2 < Ф1, так как имеется некоторый магнитный поток рассеянияФs.
Индуктивность
Собственная индуктивность. Эта индуктивность характеризует связь тока с магнитным полем, которое создано этим же током. Величина собственной индуктивности равна отношению потокосцепления самоиндукции элемента электрической цепи к току в нем:
L = Ψ/ I, (4.9) где L — индуктивность, Гн (генри). В практике определяют и учитывают в расчетах индуктивность линий электропередачи и проводной электросвязи, обмоток электрических машин, аппаратов, электромагнитов и т. д. В электротехнике, радиотехнике, электронике широко применяют устройства, обладающие собственной и взаимной индуктивностью, которую используют в определенных целях. Элемент электрической цепи, предназначенный для использования его индуктивности, называют индуктивной катушкой. На основе общего определения индуктивности [см. формулу (4.9)] и других уже известных выражений нетрудно получить формулы для подсчета индуктивности конкретных устройств: формула (4.10) — для цилиндрической или кольцевой катушки, а (4.11) — для отрезка двухпроводной линии:
L = Ψ / I = µ0 N2 S / l, (4.10) L = где а — расстояние между проводами линии; r0 — радиус поперечного сечения провода. Формула (4.10) получена в предположении, что магнитное поле катушки равномерно и один и тот же магнитный поток сцеплен со всеми витками катушки. Поэтому ее можно использовать для вычисления индуктивности цилиндрической катушки, у которой длина значительно больше диаметра (l» D). Точность результата тем больше, чем больше отношение l / D. В практике (например, радиотехнической) применяют катушки, для которых это условие часто не выполняется, поэтому для определения индуктивности применяют поправочные коэффициенты к формуле (4.10), расчетные кривые или эмпирические формулы, приводимые в справочниках. Взаимная индуктивность. Магнитная связь двух катушек с токами, расположенных вблизи друг от друга, обусловлена тем, что магнитный поток, вызванный током I1 первой катушки, сцеплен полностью или частично с витками обеих катушек. Предположим, что магнитного рассеяния нет, т. е. весь магнитный поток Ф1 сцеплен с витками обеих катушек (см. рис. 4.4, а). В данном случае имеется собственное потокосцепление первой катушки Ψ1.1 = Ф1 N1 = L1 I1 (4.12) и взаимное потокосцепление Ψ1.2 = Ф1 N2 = M1.2 I1, (4.13) которое, как и собственное, пропорционально току, создающему поток [формула (4.13) записанная по аналогии с (4.12)]. Коэффициент пропорциональности М1.2 называют взаимной индуктивностью. Аналогично выражаются собственное и взаимное потоксцепления, если они обусловлены током I2 второй катушки: Ψ2.2 = Ф2 N2 = L2 I2, (4.14) Ψ2.1 = Ф2 N1 = M2.1 I2. (4.15) Взаимная индуктивность двух индуктивных катушек — величина, равная отношению потоксцепления взаимной индукции одной катушки к току в другой катушке, которым обусловлено это потокосцепление.
На основе выражений (4.12) — (4.15) можно получить равенство M1.2M2.1 = L1L2, a используя принцип взаимности, доказать, что коэффициенты M1.2 и М2.1 одинаковы: M1.2 = М2.1 = М. Поэтому при отсутствии магнитного рассеяния, т. е. при полной магнитной связи, М = М = k Коэффициент магнитной связи k практически всегда меньше единицы(k<l), хотя теоретически он может иметь величину от 0до 1.
Магнитные свойства веществ
Интенсивность магнитного поля определяется током, которым это поле обусловлено. Это подтверждается выражением (4.3), из которого видно, что магнитная индукция в вакууме пропорциональна величине тока (μ0 =const). Если магнитное поле создается в веществе, то поле воздействует на вещество, а оно, в свою очередь, определенным образом изменяет магнитное поле. Большие исследования проблем электромагнетизма, магнитныхсвойств веществ провел известный русский физик профессор Московского университета А. Г. Столетов (1839—1896). Из его работ в этой области отметим работу по изучению намагничивания железа, свойств и характеристик ферромагнитных материалов. Намагничивание. Вещество, находящееся во внешнем магнитном поле (поле внешних токов), намагничивается и в нем возникает добавочное внутреннее магнитное поле. Оно связано с движущимися заряженными частицами (движение электронов по внутриатомным орбитам, или электронов и ядер атомов вокруг собственных осей). Движение заряженных частиц в данном случае можно рассматривать как элементарные круговые токи.
При отсутствии внешнего магнитного поля элементарные токи внутри вещества ориентированы беспорядочно, поэтому общий (суммарный) магнитный момент даже малых объемов вещества равен нулю и в окружающем пространстве магнитное поле элементарных внутренних токов не обнаруживается. Рис. 4.5 Влияние внешнего магнитного поля на элементарные токи в веществе состоит в том, что изменяется ориентация осей вращения частиц так, что их магнитные моменты оказываются направленными в одну сторону. Интенсивность и характер намагничивания у различных веществ в одинаковом внешнем магнитном поле значительно отличаются. С этой точки зрения различают диамагнитные, парамагнитные и ферромагнитные вещества. Особенность диамагнитных веществ (вода, водород, кварц, серебро, медь и др.) состоит в том, что в них магнитное поле внутренних токов (вторичное) направлено против внешнего поля, поэтому результирующее поле слабее внешнего. В веществах парамагнитных (алюминий, кислород, воздух и т. д.) и ферромагнитных (железо, кобальт, никель и некоторые их сплавы) магнитные моменты элементарных токов ориентируются в направлении внешнего магнитного поля, т. е. усиливают его. Ферромагнитные вещества имеют особо важное значение в электротехнике, поэтому их магнитные свойства далее рассмотрены подробно.
Магнитная проницаемость. Влияние свойств вещества на магнитное поле можно учесть, если в формулы (4.2); (4.3); (4.6), выражающие магнитную индукцию и магнитный поток в вакууме, ввести как множитель безразмерный коэффициент, который называется относительной магнитной проницаемостью: μ а = μ0 μr. При таком обозначении на основе выражений (4.3) и (4.6) можно записать формулы магнитной индукции и магнитного потока катушки: B = Ф = Опытами установлено, что величина μr диамагнитных и парамагнитных веществ очень мало отличается от единицы, поэтому в практических расчетах принимают для них μr = 1, т. е. используют те же выражения, что и для вакуума. Ферромагнитные вещества имеют величину μr ≥ 1. Это объясняется тем, что в них имеются области самопроизвольного намагничивания (домены), в пределах которых (объем 10-2 — 10-6 см3) элементарные магнитные моменты направлены одинаково. Складываясь, они образуют общие магнитные моменты доменов. Несмотря на самопроизвольную намагниченность отдельных областей, магнитные свойства ферромагнитных тел в пространстве, окружающем их, не обнаруживаются, так как магнитные моменты доменов ориентированы в различных направлениях. Под действием внешнего магнитного поля магнитные моменты доменов ориентируются в одну сторону и образуют общий магнитный момент тела, направленный в ту же сторону, что и внешнее магнитное поле. Эту важную особенность используют в практике, применяя ферромагнитные сердечники катушек, что позволяет резко усилить магнитную индукцию и магнитный поток при тех же значениях тока и числа витков или, иначе говоря, сконцентрировать магнитное поле в относительно малом объеме. Напряженность магнитного поля. Особенность ферромагнитных веществ состоит также и в том, чтоих магнитная проницаемость — величина не постоянная, а изменяется в зависимости от величины магнитной индукции. Это означает, что во многих случаях расчетов величина магнитной проницаемости сердечника заранее не известна и поэтому приведенные расчетные формулы [например, (4.17), (4.18)] для определения магнитной индукции или потока использовать нельзя. Решение таких задач становится возможным, если в качестве характеристики магнитного поля наряду с магнитной индукцией ввести другую величину, не зависящую от свойств среды (материала сердечника), а определяемую только величиной тока в катушке и ее размерами (величины l, S, N). Для примера возьмем кольцевую катушку и в (4.17) разделим обе части равенства на μ а: В / μ а = IN / l. Величину в левой части равенства называют напряженностью магнитного поля Н = В / μ а. (4.19) Из этой формулы видно, что напряженность магнитного поля связана с магнитной индукцией и поэтому является характеристикой магнитного поля. Но ее можно определить, учитывая только конструктивные характеристики катушки (N, l)и значение тока в ее обмотке H = IN / l, (4.20) где Н — напряженность магнитного поля, А/м (ампер/метр). У ферромагнитных веществ зависимость B = f (Н) нелинейная, магнитная проницаемость непостоянна, а изменяется с изменением магнитной индукции (μ а ≠ const), поэтому по формуле (4.19) нельзя определить величину магнитной индукции В по известному значению напряженности магнитного поля Н (или, наоборот, величину Н по известному значению В). Решение такой задачи выполняют по кривой намагничивания В = f (Н) материала сердечника (рис. 4.7). Вместе с тем формула (4.19) дает возможность определить величину абсолютной магнитной проницаемости μ а при заданном состоянии намагниченности сердечника, т. е. при известных величинах В и Н. Абсолютная магнитная проницаемость — величина, характеризующая магнитные свойства вещества, равная отношению модуля магнитной индукции к модулю напряженности магнитного поля. Из формулы (4.20) следует равенство (4.21), которое соответствует закону полного тока: IN = H l. (4.21) Ферромагнитные материалы и их свойства. Способность намагничиваться и усиливать внешнее магнитное поле — это важное, но не единственное свойство ферромагнитных веществ. Для практики большое значение имеют и другие свойства, выявляемые в процессе намагничивания.
На рис. 4.6 показана схема установки для намагничивания ферромагнитного сердечника катушки. С увеличением тока в катушке пропорционально увеличивается напряженность магнитного поля [см. формулу (4.20)].
Рис. 4.6 Рис. 4.7
Если для ряда величин напряженности измерить соответствующие им величины магнитной индукции, то можно построить характеристику первоначального намагничивания В = f (Н), которая показана на рис. 4.7 (участок 0—1). На участке 0—1 с увеличением напряженности Н увеличивается магнитная индукция В. Это объясняется тем, что магнитные моменты доменов, ранее ориентированные произвольно, принимают направление внешнего магнитного поля. Затем прирост магнитной индукции за счет внутреннего магнитного поля уменьшается, а далее полностью прекращается, т. е. наступает состояние магнитного насыщения (после точки 1) при магнитной индукции Вs. При уменьшении напряженности внешнего магнитного поля (при уменьшении тока в катушке) магнитная индукция уменьшается по кривой 1—2—3, которая не совпадает с кривой первоначального намагничивания, и при Н = 0 В = Вr. Размагничивание сердечника как бы запаздывает по сравнению с уменьшением напряженности поля. Это явление называют магнитным гистерезисом, а величину Br — остаточной магнитной индукцией. Для того чтобы полностью размагнитить сердечник, надо изменить направление тока в катушке и, увеличивая его, довести напряженность поля до величины Нс, которую называют коэрцитивной (задерживающей) силой.
При технических расчетах используют основную кривую намагничивания данного материала, близкую к кривой первоначального намагничивания, но не совпадающую с ней. На рис. 4.8 изображены основные характеристики намагничивания некоторых ферромагнитных материалов. При циклическом перемагничивании с определенной частотой ферромагнитные материалы нагреваются, что свидетельствует о затрате энергии на перемагничивание. Величина этих потерь энергии тем больше, чем больше площадь, ограниченная петлей магнитного гистерезиса.
В связи с этим различают две основные группы ферромагнитных материалов: магнитномягкие и магнитнотвердые. Магнитномягкие материалы характеризуются большими величинами начальной и максимальной магнитной проницаемости и малыми величинами коэрцитивной силы (Нс ≤ 400 А/м), легко намагничиваются и размагничиваются, имеют узкую гистерезисную петлю (рис. 4.9, а, б) и поэтому отличаются малыми потерями энергии от гистерезиса.
а) б) в) Рис. 4.9
Основные металлические магнитномягкие материалы — низкоуглеродистые стали, чугун, которые применяют для магнитопроводов, работающих в постоянных магнитных полях; листовые электротехнические стали с повышенным содержанием кремния (до 4 %), которые идут для изготовления магнитопроводов устройств переменного тока (трансформаторов, электрических машин и аппаратов). Железоникелевые сплавы — пермаллои, имеют высокую магнитную проницаемость, малую коэрцитивную силу (рис. 4.9, б), повышенное удельное сопротивление, малые потери от гистерезиса и вихревых токов и поэтому применяются в магнитных усилителях, в высокочастотных узлах радиоэлектронной аппаратуры. Сплавы на основе железа и алюминия — альсиферы используются при изготовлении сердечников, предназначенных для работы в диапазоне частот до 50 000 кГц. Присадка кремния в магнитномягких материалах увеличивает магнитную проницаемость, уменьшает коэрцитивную силу, увеличивает удельное сопротивление, чем уменьшает потери от вихревых токов; соединения окислов металлов — ферриты — изготовляют из порошкообразной смеси окиси железа (Fе203) с окислами других металлов (ZnO, МnО и т. д.) путем прессования и спекания при высоких температурах. Магнитодиэлектрики — материалы, состоящие из смеси магнитномягкого материала (карбонильное железо, пермаллои, альсиферы) с каким-либо органическим или неорганическим диэлектриком (эпоксидная или бакелитовая смола, полистирол, жидкое стекло и др.). Ферриты и магнитодиэлектрики имеют большие удельные сопротивления, малые потери от вихревых токов, что дает возможность применять их при высоких частотах. Эти материалы широко применяют для изготовления сердечников трансформаторов, аппаратуры проводной и радиосвязи, в вычислительных устройствах, автоматике. Некоторые ферриты имеют прямоугольную петлю магнитного гистерезиса, поэтому сердечники из таких материалов могут намагничиваться до насыщения при импульсе тока в обмотке и длительно оставаться намагниченными. Эти свойства позволяют применять их в запоминающих устройствах вычислительной техники. Магнитнотвердые материалы намагничиваются с трудом, но намагниченные надолго сохраняют намагниченность. Они имеют относительно большие величины остаточной магнитной индукции (0,2—2,25 Тл) и коэрцитивной силы (20 000—60 000 А/м), широкую петлю магнитного гистерезиса (рис. 4.9, в), поэтому их применяют для изготовления постоянных магнитов. К магнитнотвердым материалам относятся мартенситные высокоуглеродистые, а также легированные стали (легирующие компоненты — хром, вольфрам, кобальт, молибден). Более высокие магнитные характеристики имеют магнитнотвердые сплавы на основе железа, алюминия, никеля, легированных кобальтом, медью, титаном, ниобием. Магниты очень малых размеров или сложной формы изготовляют из металлокерамических материалов (прессование порошков и спекание при высокой температуре).
Магнитные цепи
Магнитные цепи служат для формирования рабочего магнитного потока в электрических машинах, трансформаторах, электроизмерительных приборах и других электромагнитных устройствах. Часть электромагнитного устройства, содержащую ферромагнитные тела, в которой при наличии намагничивающей силы возникает и вдоль которой замыкается магнитный поток, называют магнитной цепью. Намагничивающую силу создают обмотки с электрическим током или постоянные магниты. Часть магнитной цепи, по которой замыкается магнитный поток, изготовляют в основном из ферромагнитных материалов и называют магнитопроводом. Магнитные цепи бывают неразветвленными (рис. 4.10, 4.11) и разветвленными (рис. 4.12). Различают также магнитные, цепи однородные и неоднородные. Магнитопровод однородной цепи на всем его протяжении выполнен из одного материала и имеет одинаковое по форме и размерам поперечное сечение (рис. 4.10); в неоднородной цепи магнитопровод состоит из нескольких участков, отличающихся в общем случае по длине, поперечному сечению, материалам (рис. 4.11).
Рис. 4.10 Рис. 4.11 Рис. 4.12
Неразветвленные магнитные цепи. При расчете и конструировании магнитных цепей выбирают их формы, размеры, материалы, расположение источников намагничивающей силы (обмоток с токами, постоянных магнитов). Полагая, что конструкция магнитной цепи известна, рассмотрим прямую и обратную задачи расчета сначала в простейшем случае для однородной цепи (рис. 4.10) без учета потоков рассеяния. В прямой задаче задан магнитный поток Ф, требуется определить намагничивающую силу, необходимую для создания этого потока. Задачу решают следующим образом:1) магнитная индукция В = Ф / S; 2) напряжен-ность магнитного поля Н в сердечнике определяют по кривой намагничивания В = f (H) материала сердечника (рис. 4.8); 3) намагничивающая сила IN = H l,где l — длина магнитопровода по средней линии без учета закруглений. Обратную задачу, в которой по заданной намагничивающей силе определяют магнитный поток, решают в обратной последовательности: 1) напряженность магнитного поля H = IN / l; 2) магнитная индукция — по кривой намагничивания; 3) магнитный поток Ф = ВS. Для конкретных величин В и Н, найденных при решении задачи, можно подсчитать статическую магнитную проницаемость данного материала сердечника по формуле (4.19) μ а = В / Н. Тогда магнитная индукция B = μ а IN / l, а магнитный поток Ф = μаINS / l = = IN / (l / μ а S). Обозначив знаменатель этого выражения l / μ а S = Rм, получим для магнитного потока Ф = IN / Rм = F / Rм, (4.22) где F = IN — намагничивающая сила. Формула (4.22) похожа на выражение закона Ома для электрической цепи. По аналогии с э.д.с. Е в электрической цепи намагничивающую силу F в магнитной цепи называют магнитодвижущей силой м.д.с., а Rм — магнитным сопротивлением. Расчет магнитных цепей обычно проводят без определения магнитного сопротивления Rм. Это понятие используют в некоторых случаях при качественном рассмотрении явлений в магнитных цепях. Согласно формуле (4.21), намагничивающая сила для однородной магнитной цепи численно равна произведению напряженности магнитного поля и длины магнитопровода H l. Эту величину называют магнитным напряжением и обозначают Um (Um = Н l). Отмеченная ранее аналогия между магнитными и электрическими цепями распространяется и на цепи с неоднородными магнитопроводами. Доказано, что для магнитной цепи можно составить уравнение по закону полного тока, по форме аналогичное контурному уравнению, составленному для электрической цепи согласно второму закону Кирхгофа. В левую часть такого уравнения записывают алгебраическую сумму намагничивающих сил, встречающихся при обходе данного магнитного контура (намагничивающую силу считают положительной, если ее направление совпадает с направлением обхода); в правую часть уравнения записывают алгебраическую сумму магнитных напряжений участков магнитопровода (Нn l n = Umn), называют магнитным напряжением данного участка магнитной цепи, по аналогии с напряжением на участке электрической цепи, и считают его положительным, если направление магнитного потока на этом участке совпадает с направлением обхода
Это уравнение применяют для решения прямой задачи расчета неоднородной магнитной цепи. Неразветвленную цепь в этом случае делят на однородные участки и для каждого из них определяют магнитную индукциюВn, а затем находят значения напряженности магнитного поля Нn и магнитного напряжения Umn. По уравнению (4.23) определяют намагничивающую силу F, необходимую для получения заданного магнитного потока. Обратную задачу — определение магнитного потока по заданным намагничивающим силам — нельзя решить так же просто, как для однородной цепи, так как неизвестно распределение магнитных напряжений между участками. Для решения обратной задачи применяют графоаналитические методы, которые здесь не рассматриваются. Разветвленные магнитные цепи. В разветвленной магнитной цепи, по аналогии с электрической цепью, можно выделить контуры, ветви и отметить узлы. Магнитные потоки в общем случае различны в различных ветвях (рис. 4.12). Для разветвленных магнитных цепей можно составить узловые уравнения (ΣФ = 0) и контурные уравнения (ΣФ = ΣН l).Алгебраическое решение системы узловых и контурных уравнений магнитной цепи обычными способами невозможно, так как эта система нелинейная. Поэтому в практике применяют графические и графоаналитические методы расчета разветвленных магнитных цепей. Однако симметричную разветвленную магнитную цепь (рис. 4.12) условно можно разделить на контуры так, что во всех Участках выделенного контура магнитный поток будет один и тот жe. Кроме того, предполагается симметричное расположение обмоток с токами. Расчет симметричной магнитной цепи можно свести к расчету одного контура в том порядке, в котором рассчитывают неразветвленные цепи.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.191.241 (0.015 с.) |

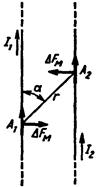 Закон Ампера. В 1820 г. Ампер установил закон, выражающий силу взаимодействия электрических токов.
Закон Ампера. В 1820 г. Ампер установил закон, выражающий силу взаимодействия электрических токов. , (4.1)
, (4.1)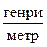 (Гн/м) – магнитная постоянная.
(Гн/м) – магнитная постоянная.
 и скорости v частицы.
и скорости v частицы. =
=  =
=  .
.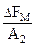 =
=  ,
,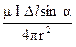 , (4.2)
, (4.2)
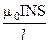 (4.6)
(4.6)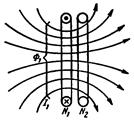
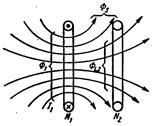
 ln
ln  , (4.11)
, (4.11)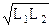 . В действительности некоторая часть линий магнитной индукции первой катушки не образует магнитной связи со второй катушкой. Этими линиями образуется магнитный поток рассеяния Фs. В реальных устройствах, где используется магнитная (индуктивная) связь, магнитный поток рассеяния должен быть по возможности уменьшен. Однако потоки рассеяния уменьшить до нуля невозможно, поэтому взаимная индуктивность выражается формулой
. В действительности некоторая часть линий магнитной индукции первой катушки не образует магнитной связи со второй катушкой. Этими линиями образуется магнитный поток рассеяния Фs. В реальных устройствах, где используется магнитная (индуктивная) связь, магнитный поток рассеяния должен быть по возможности уменьшен. Однако потоки рассеяния уменьшить до нуля невозможно, поэтому взаимная индуктивность выражается формулой
 ; (4.17)
; (4.17) . (4.18)
. (4.18)

 Изменяя ток в катушке по величине и направлению, можно получить данные для построения замкнутой кривой В = f (Н), которую называют петлей магнитного гистерезиса.
Изменяя ток в катушке по величине и направлению, можно получить данные для построения замкнутой кривой В = f (Н), которую называют петлей магнитного гистерезиса.


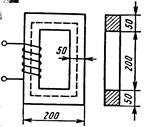


 . (4.23)
. (4.23)


