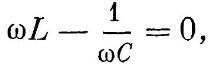Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия электромагнитных волнСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Как показывает опыт, электромагнитные волны могут производить различные действия: нагревание тел при поглощении света, вырывание электронов с поверхности металла под действием света (фотоэффект). Это свидетельствует о том, что электромагнитные волны переносят энергию. Эта энергия заключена в распространяющихся в пространстве электрическом и магнитном полях. В курсе электричества и магнетизма было показано, что объемная плотность энергии электрического поля равна
а магнитного поля –
где
Так как модули вектора напряженности электрического и индукции магнитного поля в электромагнитной волне связаны соотношением
Из (1.4) видно, что объемная плотность энергии складывается из двух равных по величине вкладов, соответствующих плотностям энергии электрического и магнитного полей. Это обусловлено тем, что в электромагнитной волне происходят взаимные превращения электрического и магнитного полей. Эти процессы идут одновременно, и электрическое и магнитное поля выступают как равноправные «партнеры». Плотность энергии электромагнитного поля можно представить в виде:
Формула (1.5) характеризует плотность энергии в любой момент времени в любой точке пространства. Если выделить площадку с площадью s, ориентированную перпендикулярно направлению распространения волны, то за малое время Δ t через площадку пройдет энергия
где Плотностью потока энергии называют электромагнитную энергию, переносимую волной за единицу времени через поверхность единичной площади, перпендикулярной к направлению распространения волны:
Подставляя в последнее соотношение выражения для
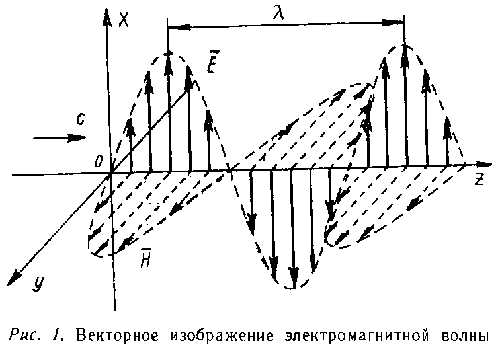
Электромагнитные волны Передача энергии и информации от передатчика к приемнику происходит при помощи электромагнитных волн (ЭМВ) или радиоволн, которые представляют собой распространяющееся в пространстве электромагнитное поле высокой частоты. Электромагнитное поле — это совокупность взаимосвязанных электрического (Е) и магнитного (Н) полей. Взаимосвязь заключается в том, что изменения напряженности электрического поля приводят к появлению магнитного поля, а изменяющееся магнитное поле вызывает появление электрического. На рис. 1 дано векторное изображение электромагнитной волны (ЭМВ), распространяющейся вдоль оси z. Стрелками — векторами* показаны направление и величина (напряженность) полей E и H в разных точках на оси z в фиксированный момент времени. Вся картина движется вдоль оси z со скоростью света с = 300000 км/сек. Направление распространения связано по правилу винта с направлением поворота вектора E к вектору H по кратчайшему пути. Расстояние между двумя соседними гребнями (или впадинами) изменений поля E называется длиной волны λ. Длина волны связана с частотой f передатчика формулой:
* Вектором A называется отрезок прямой, имеющий длину A и заданное направление. Между величинами E и H в ЭМВ существует однозначная зависимость
где μ и ε — магнитная и диэлектрическая проницаемости среды. Величину электромагнитного поля оценивают поэтому напряженностью только одного, чаще электрического поля E в вольтах на метр (в/м).
Поляризация. Волна называется вертикально-поляризованной, если плоскость, проходящая через направление распространения и вектор E вертикальна. Если вектор E расположен в горизонтальной плоскости, то волна называется горизонтально-поляризованной. В общем случае вектор E может иметь и вертикальную и горизонтальную составляющие. Излучение ЭМВ. Передатчик излучает ЭМВ при помощи передающей антенны, которая преобразует высокочастотную энергию в энергию электромагнитного поля. Для эффективного излучения ЭМВ размеры антенны должны быть сравнимы с длиной волны. Например, провод длиной 1 м будет хорошим излучателем на диапазоне 2 м и малоэффективным на диапазоне 80 м. В свободно распространяющейся ЭМВ происходит непрерывный переход энергии электрического поля в энергию магнитного поля и обратно. Напряженность поля на расстоянии R [ км ] от антенны, излучающей мощность PΣ [ вт ] равномерно во всех направлениях, равна [11]:
В свободном пространстве напряженность поля пропорциональна квадратному корню из мощности и обратно пропорциональна расстоянию. В рассмотренном случае волна распространяется во все стороны равномерно, и мы имеем так называемый сферический фронт* волны. На больших расстояниях сферический фронт можно считать плоским, а волну — плоской волной. Заметим, что перпендикуляр к поверхности фронта волны совпадает с направлением распространения, — это используется в радиопеленгации. Вертикально-поляризованные волны излучаются вертикальными антеннами типа штырь, луч, вертикальным симметричным вибратором, диско-конусной антенной. Горизонтально-поляризованные волны излучают горизонтальный диполь, петлевой вибратор, «квадрат». * Фронт—это поверхность равных фаз, например, максимумов поля Е. Индуктивность Индуктивностью (от латинского inductio - наведение, побуждение), называется величина, характеризующая связь между изменением тока в электрической цепи и возникающей при этом ЭДС (электродвижущей силы) самоиндукции. Индуктивность обозначается большой латинской буквой «L», в честь немецкого физика Ленца. Термин индуктивности предложил в 1886 году Оливер Хевисайд. Величина магнитного потока, проходящего через контур, связана с силой тока следующим образом: Φ = LI. Коэффициент пропорциональности L называется коэффициентом самоиндукции контура или просто индуктивностью. Значение индуктивности зависит от размеров и формы контура, а также от магнитной проницаемости среды. Единицей измерения индуктивности является Генри (Гн). Дополнительные величины: мГн, мкГн. Зная индуктивность, изменение силы тока и время этого изменения, можно найти ЭДС самоиндукции, которая возникает в контуре:
Через индуктивность выражают также энергию магнитного поля тока:
Соответственно чем больше индукция, тем больше магнитная энергия, накапливаемая в пространстве вокруг контура с током. Индуктивность является своеобразным аналогом кинетической энергии в электричестве. 39. Закон Ома для цепи переменного тока где
Если значения емкости С и индуктивности L исследуемого участка цепи переменного тока пренебрежимо малы, то, используя закон Ома, найдем напряжение на участке цепи, сопротивление которого r:
где Если индуктивность исследуемого участка пренебрежимо мала (L ≈ 0), а значением емкости пренебречь нельзя, то результаты расчета будут несколько иными. Зная, что мгновенное значение силы тока определяется выражением
можно найти количество электричества, протекающее за время t через поперечное сечение исследуемого участка:
Подставляя в это выражение значение переменного тока, получим:
или после интегрирования:
Постоянная интегрирования имеет смысл заряда, которым обладает конденсатор до включения его в цепь. Если в цепь включают незаряженный конденсатор, то можно считать С 0 = 0 и тогда
Так как емкость конденсатора выражается формулой
то напряжение на концах участка цепи, содержащего емкость, определим по формуле:
Сравнивая формулы для силы тока и напряжения, замечаем, что на участке цепи, содержащем емкость, значение напряжения отстает от значения силы тока по фазе на π/2, то есть сила тока достигает максимума в тот момент, когда напряжение на исследуемом участке обращается в нуль. Амплитудное значение напряжения для указанного случая определяется выражением
Снова используя закон Ома для участка цепи, получим формулу, позволяющую вычислить емкостное сопротивление участка:
Приведем расчет участка цепи переменного тока, содержащего индуктивность; значение емкости этого участка учитывать не будем вследствие его малости. Зная, что при изменении тока в катушке индуктивности в ней возникает ЭДС самоиндукции, запишем для этого случая закон Ома:
Пренебрегая активным сопротивлением исследуемого участка (r = 0) и учитывая, что ЭДС самоиндукции определяется по закону
получим:
Для тока, изменяющегося синусоидально, найдем:
или
Сравнивая выражения для тока и напряжения, видим, что напряжение на концах участка цепи, содержащего индуктивность, опережает ток в нем по фазе на π/2. Амплитудное значение напряжения для этого случая определим по формуле:
Используя закон Ома, найдем формулу для расчета индуктивного сопротивления участка цепи:
Расчет участка цепи переменного тока, содержащего активное сопротивление, индуктивность и емкость, проведенный с привлечением метода векторных диаграмм, дает для амплитудного значения напряжения на концах этого участка следующее выражение:
Сопротивление этого участка определяется формулой
где R — полное сопротивление исследуемого участка цепи, r — активное сопротивление этого участка, Максимального значения переменный ток достигает при условии
т. е. при значении частоты переменного тока
что соответствует периоду колебаний
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1487; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.242.169 (0.006 с.) |

 ,
,
 ,
,
 и
и  – электрическая и магнитная постоянные. Таким образом, полная плотность энергии электромагнитной волны равна
– электрическая и магнитная постоянные. Таким образом, полная плотность энергии электромагнитной волны равна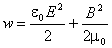 .
.
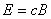 , то полную энергию можно выразить только через напряженность электрического поля или индукцию магнитного поля:
, то полную энергию можно выразить только через напряженность электрического поля или индукцию магнитного поля: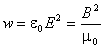 .
.
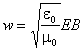 .
.
 , равная
, равная ,
, – скорость электромагнитной волны в вакууме.
– скорость электромагнитной волны в вакууме. .
.
 и
и 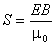 .
.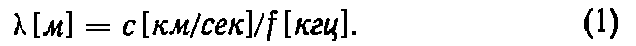

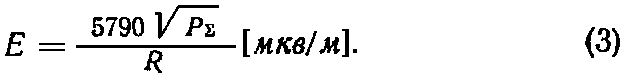
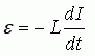


 — амплитудное значение ЭДС; ω — циклическая частота. В этом случае и сила тока, возбуждаемого во внешней части цепи, будет изменяться по такому же закону:
— амплитудное значение ЭДС; ω — циклическая частота. В этом случае и сила тока, возбуждаемого во внешней части цепи, будет изменяться по такому же закону: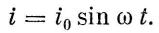

 — амплитудное значение напряжения. Из полученного следует, что если на некотором участке цепи практически отсутствуют индуктивность и емкость, то переменный ток и напряжение на концах этого участка совпадают по фазе.
— амплитудное значение напряжения. Из полученного следует, что если на некотором участке цепи практически отсутствуют индуктивность и емкость, то переменный ток и напряжение на концах этого участка совпадают по фазе.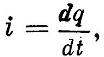





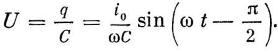
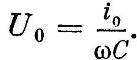






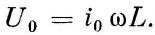


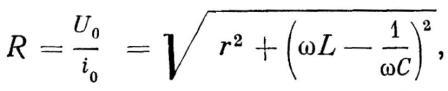
 — его реактивное сопротивление.
— его реактивное сопротивление.