
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрическое поле. Напряженность поля . Принцип суперпозиции.Содержание книги
Поиск на нашем сайте
Взаимодействие между покоящимися зар. осуществляется посредством Эл.п. (электро-статического поля). понятие Эл.п. ввел Фарадей. Неподвижный Эл.зар. изменяет свойство пространства и создает Эл.п. Оно проявляется по действию на пробный зар. Отношение силы действующей со стороны поля на пробный зар. не зависит от величины этого зар. и может хар-ть само Эл.п., тогда приходим к характеристике поля – напряженности: Эл.п. эсть векторная силовая характеристика поля = отношению силы, действующей на зар. со стороны поля,к зар., т.е.:
Если известна Е, то сила со стороны поля действующая на зар. q =: Сила F, действующая на пробный зар. q в данной точке поля, = векторной сумме сил каждого зар. в отдельности, т.е.:
Напряженность Эл.п. системы зар. = векторной сумме напряженностей полей, создаваемых каждым зар. в отдельности.
Если непрерывно распределенный зар. т.е.:
3. Теорема Гауса. Её применение для расчёта электрических полей. Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью.
Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния[1] в законе Кулона «из первых принципов», а не постулировать ее (или не находить эмпирически). В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике. Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика. Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
4.Потенциал поля.
Потенциал поля точки q на расстоянии r от зар. будет считаться равным:
С учетом такого обозначения имеем: Работа сил Эл.п. при перемещении зар. численно = произведению величине этого зар. на разность потенциалов в начальной и конечной точке поля. Пусть точка 2 лежит в бесконечности, тогда можем написать:
Разность потенциалов(или напряжение).
|
|||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.185.58 (0.01 с.) |

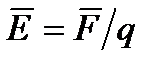 , q≷0, Напряженность поля численно = силе, действующей на единичный «+» зар.
, q≷0, Напряженность поля численно = силе, действующей на единичный «+» зар.  , когда q=+1. Единицы измерения напряжения
, когда q=+1. Единицы измерения напряжения  ,
, 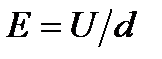 . Найдем напряжение поля точечного зар. q, находящейся в точке. Хар. вектором
. Найдем напряжение поля точечного зар. q, находящейся в точке. Хар. вектором  в среде, по З.Кулона можем записать
в среде, по З.Кулона можем записать
 ,
,  - созд. точечный зар.
- созд. точечный зар.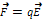
 , помножим на
, помножим на 
 … т.е.
… т.е.  - принцип суперпозиции.
- принцип суперпозиции.

 .Эл.п. графически изображается с помощью линий напряженности Е, силовых линий, линий Е, метод предложил Фарадей. Линии напряженности это кривые, касательный к которым в каждой точке совпадают с направлением вектора напряженности в данной точке. Линии напряженности начинаются на «+» зар. и заканчиваются на «-» или уходят в
.Эл.п. графически изображается с помощью линий напряженности Е, силовых линий, линий Е, метод предложил Фарадей. Линии напряженности это кривые, касательный к которым в каждой точке совпадают с направлением вектора напряженности в данной точке. Линии напряженности начинаются на «+» зар. и заканчиваются на «-» или уходят в  . Густота силовых линий,т.е. число линий на ед. площади поверхности перпендикулярной к линиям. Она выбирается так, что количество линий пронизывающих ед. площади поверхности равно или пропорционально
. Густота силовых линий,т.е. число линий на ед. площади поверхности перпендикулярной к линиям. Она выбирается так, что количество линий пронизывающих ед. площади поверхности равно или пропорционально  . По силовым линиям можно судить о величине и направлении вектора в разных точках пространства. Рассмотрим примеры силовых линий:
. По силовым линиям можно судить о величине и направлении вектора в разных точках пространства. Рассмотрим примеры силовых линий:

 -поток вектора напряжённости электрического поля через замкнутую поверхность S.
-поток вектора напряжённости электрического поля через замкнутую поверхность S.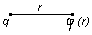 Рассмотрим точку q.
Рассмотрим точку q.


 . Потенциал
. Потенциал  есть скалярная энергетическая характеристика Эл.п., численно = потенциальной энергии единичного «+» зар. в данной точке поля:
есть скалярная энергетическая характеристика Эл.п., численно = потенциальной энергии единичного «+» зар. в данной точке поля:  =+1. Потенциал поля численно = отношению потенциальной энергии зар. данной точки поля к зар.(здесь знак зар. учитывается). Работу сил Эл.п. выразить через разность потенциалов:
=+1. Потенциал поля численно = отношению потенциальной энергии зар. данной точки поля к зар.(здесь знак зар. учитывается). Работу сил Эл.п. выразить через разность потенциалов:  , где
, где 


 . Потенциал Эл.п.
. Потенциал Эл.п.  численно = работе сил поля при перемещении ед. «+» зар. из данной точки поля в
численно = работе сил поля при перемещении ед. «+» зар. из данной точки поля в  , тогда
, тогда  *U U=
*U U=  - потенциал между точками 1и 2 измеряется работой совершенной силами поля при перемещении единичного «+» зар. из точки 1 в 2 по любому пути.
- потенциал между точками 1и 2 измеряется работой совершенной силами поля при перемещении единичного «+» зар. из точки 1 в 2 по любому пути. 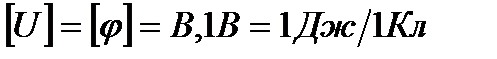 . Для потенциала справедлив принцип суперпозиции: потенциал поля
. Для потенциала справедлив принцип суперпозиции: потенциал поля 
 Эквипотенциальная поверхность - пов. одинакового, разного потенциала, на которой
Эквипотенциальная поверхность - пов. одинакового, разного потенциала, на которой  , линии напряженности Е ортогональны (в частности перпендикулярны) к эквипотенциальной пов.
, линии напряженности Е ортогональны (в частности перпендикулярны) к эквипотенциальной пов.


