
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ток электролита. Закон фарадея для электролиза.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Электрический ток в электролитах представляет собой перемещение ионов обоих знаков в противоположных направлениях. Положительные ионы движутся к отрицательному электроду (катоду), отрицательные ионы – к положительному электроду (аноду). Ионы обоих знаков появляются в водных растворах солей, кислот и щелочей в результате расщепления части нейтральных молекул. Это явление называется электролитической диссоциацией. При подключении электродов к источнику тока ионы под действием электрического поля начинают упорядоченное движение: положительные ионы меди движутся к катоду, а отрицательно заряженные ионы хлора – к аноду. Масса выделившегося на электроде вещества равна массе всех ионов, пришедших к электроду:
Электро́лиз — физико-химический процесс, состоящий в выделении на электродах составных частей растворённых веществ или других веществ, являющихся результатом вторичных реакций на электродах, который возникает при прохождении электрического тока через раствор либо расплав электролита. В 1832 году Фарадей установил, что масса m вещества, выделившегося на электроде, прямо пропорциональна электрическому заряду q, прошедшему через электролит:
если через электролит пропускается в течение времени t постоянный ток с силой тока I. Коэффициент пропорциональности называется электрохимическим эквивалентом вещества. Он численно равен массе вещества, выделившегося при прохождении через электролит единичного электрического заряда, и зависит от химической природы вещества. 1-вый закон Фарадэя:
2-рой закон Фарадэя:
Закон Ома для электролитов. Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (то есть проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
где R = const. Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Это соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А. Проводники, подчиняющиеся закону Ома, называются линейными. Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
IR = U12 = φ1 – φ2 + По закону Ома, IR = Δφcd. Участок (ab) содержит источник тока с ЭДС, равной Сложив оба равенства, получим:I(R + r) = Δφcd + Δφab + Но Δφcd = Δφba = – Δφab. Поэтому Закон Ома для аднароднага ўчастка электрычнага цепи постоянного тока кажа, что сила тока прямо пропорциональна напряжению на участке и адваротна прапарцыянальна супраціўленню гэтага ўчастка. Гэта залежнасць выражаецца формулай:
ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ В обычных условиях газ - это диэлектрик, т.е. состоит из нейтральных атомов и молекул и не содержит свободных носителей эл.тока. Газ-проводник - это ионизированный газ. Ионизированный газ обладает электронно-ионной проводимостью.Воздух является диэлектриком в линиях электропередач, в воздушных конденсаторах, в контактных выключателях. Воздух является проводником при возникновении молнии, электрической искры, при возникновении сварочной дуги. Ионизация газа - это распад нейтральных атомов или молекул на положительные ионы и электроны путем отрыва электронов от атомов. Ионизация происходит при нагревании газа или воздействия излучений (УФ, рентген, радиоактивное) и объясняется распадом атомов и молекул при столкновениях на высоких скоростях. Газовый разряд- это эл.ток в ионизированных газах. Носителями зарядов являются положительные ионы и электроны. Газовый разряд наблюдается в газоразрядных трубках (лампах) при воздействии электрического или магнитного поля. Существует самостоятельный и несамостоятельный газовый разряд.Несамостоятельный газовый разряд- если действие ионизатора прекратить, то прекратится и разряд.Когда разряд достигает насыщения - график становится горизонтальным. Здесь электропроводность газа вызвана лишь действием ионизатора. Самостоятельный газовый разряд - в этом случае газовый разряд продолжается и после прекращения действия внешнего ионизатора за счет ионов и электронов, возникших в результате ударной ионизации (= ионизации эл. удара); возникает при увеличении разности потенциалов между электродами (возникает электронная лавина).
Несамостоятельный газовый разряд может переходить в самостоятельный газовый разряд при [Ua = U ]зажигания. Электрический пробой газа- процесс перехода несамостоятельного газового разряда в самостоятельный. Плазма- это четвертое агрегатное состояние вещества с высокой степенью ионизации за счет столкновения молекул на большой скорости при высокой температуре; встречается в природе:ионосфера - слабо ионизированная плазма, Солнце - полностью ионизированная плазма; искусственная плазма - в газоразрядных лампах.Плазма бывает:Низкотемпературная - при температурах меньше 100 000К;высокотемпературная - при температурах больше 100 000К. Вариант 20 Га́зовый разря́д — совокупность процессов, возникающих при протекании электрического тока через вещество, находящееся в газообразном состоянии. Обычно протекание тока становится возможным только после достаточной ионизации газа и образования плазмы. Ионизация происходит за счёт столкновений электронов, ускорившихся в электромагнитном поле, сатомами газа. При этом возникает лавинное увеличение числа заряженных частиц, поскольку в процессе ионизации образуются новые электроны, которые тоже после ускорения начинают участвовать в соударениях с атомами, вызывая их ионизацию. Для возникновения и поддержания газового разряда требуется существование электрического поля, так как плазма может существовать только если электроны приобретают во внешнем поле энергию, достаточную для ионизации атомов, и количество образованных ионов превышает число рекомбинировавших ионов. Ток в газе, возникающий при наличии внешнего ионизатора называется несамостоятельным газовым разрядом. Газовый разряд который продолжается после прекращения действия внешнего ионизатора называется самостоятельным газовым разрядом. Напряжение при котором возникает самостоятельный разряд,- напряжение пробоя. Виды газовых разрядов: Тихий разряд. Весьма низкая плотность тока в газе, не сопровождается испусканием света или звука. Тлеющий разряд. Ток, проходящий через разряжённый газ при высоких напряжениях. Сопровождается холодным свечением Дуговой разряд. Характеризуется большим плотностями тока (тысячи ампер на мм.кв.), сравнительно небольшими напряжениями(десятки вольт), сопровождается сильным свечением и температурой(3000-6000 Г.Ц.) Искровой разряд. Электрический пробой газов при кратковременном лавинообразном увеличении количества ионов в нём. Коронный разряд. Слабые электрические токи в газах при атмосферном давлении, вызванные сильно неоднородным полем при больших значениях напряжённости поля. Наблюдается слабое свечение в области электродов Сильно ионизированный газ, содержащий практически одинаковое количество заряжённых частиц обоих знаков, называют плазмой. От способа получения делится на высокотемпературную и газоразрядную Магнитное поле Магнитное поле, как и эл-кое, изображается магнитными силовыми линиями – линиями (в-р) B. Линии магнитной индукции (в-р) B – это линии, касат к кот в каждой точке совпадают с напр в-ра B. Линии (в-р) B всегда замкнуты, что указывает на вихревой характер магнитного поля, на отсутствие магнитных зарядов, на кот могли бы начинаться и заканчиваться силовые линии. По густоте силовых линий судят о величине магнитного поля; там где силовые линии редкие – магнитное поле слабое.
Линии индукции прямолинейного проводника с током представляют собой концентрические окружности, центры которых лежат на оси тока. При поступательном движении правого винта направление вращения рукоятки винта указывает направление силовых линий. 1. Электронный орбитальный магнитный момент – из-за вращения эл-нов вокруг ядер.
2. Электронный спиновой магнитный момент.
Если известна Е, то сила со стороны поля действующая на зар. q =: Сила F, действующая на пробный зар. q в данной точке поля, = векторной сумме сил каждого зар. в отдельности, т.е.:
Напряженность Эл.п. системы зар. = векторной сумме напряженностей полей, создаваемых каждым зар. в отдельности.
Если непрерывно распределенный зар. т.е.:
Закон Био-Савара-Лапласа Взаимодействие между покоящимися зар. осуществляется посредством Эл.п. (электро-статического поля). понятие Эл.п. ввел Фарадей. Неподвижный Эл.зар. изменяет свойство пространства и создает Эл.п. Оно проявляется по действию на пробный зар. Отношение силы действующей со стороны поля на пробный зар. не зависит от величины этого зар. и может хар-ть само Эл.п., тогда приходим к характеристике поля – напряженности: Эл.п. эсть векторная силовая характеристика поля = отношению силы, действующей на зар. со стороны поля,к зар., т.е.:
Если известна Е, то сила со стороны поля действующая на зар. q =: Сила F, действующая на пробный зар. q в данной точке поля, = векторной сумме сил каждого зар. в отдельности, т.е.:
Напряженность Эл.п. системы зар. = векторной сумме напряженностей полей, создаваемых каждым зар. в отдельности.
Если непрерывно распределенный зар. т.е.:
Закон Ампера Ампер эксп-но установил, что сила d(в-р)F действ на элемент тока Id(в-р)l с индукцией (в-р) B равна: Рассмотрим работу перемещения проводника с током в магнитном поле: На проводник с током будет действовать сила Ампера и проводник передвинется: Элементарная работа при перемещении проводника:
Конечная работа это: Теорема о циркуляции Теорема о циркуляции вектора магнитной индукции в вакууме (
Так как С учетом последнего соотношения теорема о циркуляции вектора магнитной индукции принимает вид:
Циркуляция вектора напряженности магнитного поля вдоль произвольного замкнутого конура равна результирующему макро току через поверхность ограниченного этим контуром. Для изотропных магнетиков связь намагниченности j и напряженности Н магнитного поля. Т.е. Закон полного тока (теорема о циркуляции вектора магнитной индукции):циркуляция вдоль замкнутого контура вектора магнитной индукции в вакууме равна произведению магнитной постояннойm0 на алгебраическую сумму токовохватываемых этим контуром:
 , , 
Теорема о циркуляции вектора магнитной индукции есть следствие з-на БСЛ, но она допуск обобщение на поля и люб среды. При таком обобщении эта теорема – одно из обобщ электродинамики Максвелла:
Вопрос 25 Рассмотрим соленоид длиной l, который имеет N витков, и по которому течет ток (рис. 1). Будем считать длину соленоида во много раз больше, чем диаметр его витков. Экспериментальное изучение магнитного поля соленоида (см. главу "магнитное поле и его характеристики") показывает, что внутри соленоида поле однородно, вне соленоида — неоднородно и практически отсутствует. На рис. 1 даны линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем магнитная индукция вне его меньше. Поэтому приближенно можно полагать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а поле соленоида можно не учитывать. Для вычисления магнитной индукции В выберем замкнутый прямоугольный контур ABCDA, как показано на рис. 1. Циркуляция вектора В по замкнутому контуру ABCDA, который охватывает все N витков, используя формулу циркуляции вектора В, будет
Интеграл по ABCDA можно разложить на четыре интеграла: по АВ, ВС, CD и DA. На участках АВ и CD контур и линии магнитной индукции перпендикулярны: B l =0. На участке вне соленоида B=0. На участке DA циркуляция вектора В равна В l (контур и линии магнитной индукции совпадают); значит,
Из (1) приходим к формуле магнитной индукции поля внутри соленоида (в вакууме):
Мы видим, что поле внутри соленоида однородно (при расчетах пренебрегают краевыми эффектами в областях, прилегающих к торцам соленоида). Но отметим, что вывод этой формулы не совсем корректен (поскольку линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно найти поле внутри соленоида можно, используя закон Био — Савара — Лапласа; в результате получается такая же формула (2). Важное практическое значение имеет также магнитное поле тороида — кольцевой катушки, у которой витки намотаны на сердечник, который имеет форму тора (рис. 2). Магнитное поле, как известно из опыта, сосредоточено внутри тороида, а вне его поле равно нулю. В данном случае линии магнитной индукции, как следует из соображений симметрии, есть окружности, у которых центры расположены по оси тороида. В качестве контура возьмем одну такую окружность радиуса r. Тогда, используя теорему о циркуляции, B•2πr=μ0NI, откуда следует, что магнитная индукция внутри тороида (в вакууме)
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.143.183 (0.013 с.) |

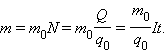

 ,
,  ,
,  ,
, 


 = Δφ12 +
= Δφ12 + 



 , где Ls – спиновой механический момент
, где Ls – спиновой механический момент
 , помножим на
, помножим на 
 … т.е.
… т.е.  - принцип суперпозиции.
- принцип суперпозиции.

 .Эл.п. графически изображается с помощью линий напряженности Е, силовых линий, линий Е, метод предложил Фарадей.
.Эл.п. графически изображается с помощью линий напряженности Е, силовых линий, линий Е, метод предложил Фарадей.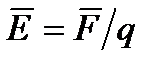 , q≷0, Напряженность поля численно = силе, действующей на единичный «+» зар.
, q≷0, Напряженность поля численно = силе, действующей на единичный «+» зар.  , когда q=+1. Единицы измерения напряжения
, когда q=+1. Единицы измерения напряжения  ,
, 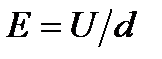 . Найдем напряжение поля точечного зар. q, находящейся в точке. Хар. вектором
. Найдем напряжение поля точечного зар. q, находящейся в точке. Хар. вектором  в среде, по З.Кулона можем записать
в среде, по З.Кулона можем записать
 ,
,  - созд. точечный зар.
- созд. точечный зар. . Густота силовых линий,т.е. число линий на ед. площади поверхности перпендикулярной к линиям. Она выбирается так, что количество линий пронизывающих ед. площади поверхности равно или пропорционально
. Густота силовых линий,т.е. число линий на ед. площади поверхности перпендикулярной к линиям. Она выбирается так, что количество линий пронизывающих ед. площади поверхности равно или пропорционально  . По силовым линиям можно судить о величине и направлении вектора в разных точках пространства. Рассмотрим примеры силовых линий:
. По силовым линиям можно судить о величине и направлении вектора в разных точках пространства. Рассмотрим примеры силовых линий:

 – закон Ампера (сила Ампера). Если проводник прямолинейный и магнитное поле однородное (одинаковое в каждой точке), интегрируя последнее выражение, получаем:
– закон Ампера (сила Ампера). Если проводник прямолинейный и магнитное поле однородное (одинаковое в каждой точке), интегрируя последнее выражение, получаем:  . Направление силы Ампера (в-р)F опр по правилу в-рного произведения. Сила (в-р)F ┴-а пл-сти, в кот лежат в-ры l и B и напр силы (в-р)F опред правилом правого винта: «если рукоятка правого винта вращается от первого вектора l ко второму ве-ру B на кратчайший угол, то поступательное движ винта указ направление силы (в-р)F». Модуль силы Ампера:
. Направление силы Ампера (в-р)F опр по правилу в-рного произведения. Сила (в-р)F ┴-а пл-сти, в кот лежат в-ры l и B и напр силы (в-р)F опред правилом правого винта: «если рукоятка правого винта вращается от первого вектора l ко второму ве-ру B на кратчайший угол, то поступательное движ винта указ направление силы (в-р)F». Модуль силы Ампера: 

 ,
, 
 ,
, 
 ) допускает обобщение на магнитное поле в веществе в виде:
) допускает обобщение на магнитное поле в веществе в виде:  , где Iмакро и Iмикро – алгебраическая сумма макро и микро токов через поверхность S ограниченных контуром L. Покажем теперь, что Iмикро связан с намагниченностью j:
, где Iмакро и Iмикро – алгебраическая сумма макро и микро токов через поверхность S ограниченных контуром L. Покажем теперь, что Iмикро связан с намагниченностью j: 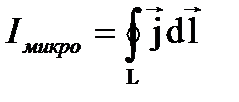
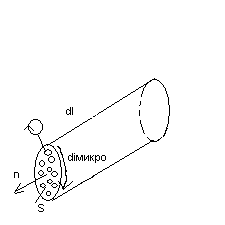 Т.е. сумма микро токов через поверхность S ограниченных контуром L равна циркуляции вектора намагниченности j. Рассмотрим прямой круговой намагниченный цилиндр длинной dl и площадью поперечного сечения S. Молекулярные токи внутри цилиндра текут в противоположные стороны и поэтому взаимноскомпенсированы. Нескомпенсированы только те токи, которые выходят на поверхность цилиндра и ни складываются в поверхностный ток
Т.е. сумма микро токов через поверхность S ограниченных контуром L равна циркуляции вектора намагниченности j. Рассмотрим прямой круговой намагниченный цилиндр длинной dl и площадью поперечного сечения S. Молекулярные токи внутри цилиндра текут в противоположные стороны и поэтому взаимноскомпенсированы. Нескомпенсированы только те токи, которые выходят на поверхность цилиндра и ни складываются в поверхностный ток 
 С другой стороны полный магнитный момент цилиндра по опр намагниченности равен:
С другой стороны полный магнитный момент цилиндра по опр намагниченности равен:  ,
, 
 и
и  направлены в одну сторону, то dIмикро=jdl. Вклад в циркуляцию намагниченность дадут только те токи, которые нанизаны как бусы на нитку. Тогда окончательно можно написать:
направлены в одну сторону, то dIмикро=jdl. Вклад в циркуляцию намагниченность дадут только те токи, которые нанизаны как бусы на нитку. Тогда окончательно можно написать:  ,
, 
 ,
,  - теорема о циркуляции магнитного поля
- теорема о циркуляции магнитного поля χ—безразмерная величина – магнитная восприимчивость среды или вещества. Подставим
χ—безразмерная величина – магнитная восприимчивость среды или вещества. Подставим  в выражении для
в выражении для  :
:  ,
,  ,
, 
 . Выбор направления обхода контур L согласовывается с направлением тока по правилу правого винта. Ток берётся с «+»если с острия тока I обход контура совершается против часовой стрелки иначе «-». Если замкнутый контур не охватывает проводник с током, то циркуляция вектора равна В=0. Рассмотрим доказательство для магнитного поля бесконечного прямолинейного проводника с током I в вакууме. За контур L возьмем линии индукции В находящихся на r от оси проводника с током.
. Выбор направления обхода контур L согласовывается с направлением тока по правилу правого винта. Ток берётся с «+»если с острия тока I обход контура совершается против часовой стрелки иначе «-». Если замкнутый контур не охватывает проводник с током, то циркуляция вектора равна В=0. Рассмотрим доказательство для магнитного поля бесконечного прямолинейного проводника с током I в вакууме. За контур L возьмем линии индукции В находящихся на r от оси проводника с током. . Т о цирк в-ра магн инд позвол магн поля различных конструкций токов.
. Т о цирк в-ра магн инд позвол магн поля различных конструкций токов.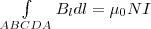
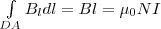 (1)
(1) (2)
(2) где N — число витков тороида. Если контур проходит вне тороида, то токов он не охватывает и B•2πr = 0. Следовательно, что поле вне тороида отсутствует (что показывает и опыт).
где N — число витков тороида. Если контур проходит вне тороида, то токов он не охватывает и B•2πr = 0. Следовательно, что поле вне тороида отсутствует (что показывает и опыт).



