
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие 7. Последовательные независимые испытания.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Краткая теоретическая часть В настоящем разделе мы изучим основные закономерности, относящиеся к одной из важнейших схем теории вероятностей — схеме последовательных независимых испытаний. В это понятие мы вкладываем следующий смысл. Под испытанием(опытом) мы станем понимать осуществление определенного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства U элементарных событий. Математической моделью последовательности п испытаний является новое пространство Предположим, что для s-го испытания пространство U разбито на k несовместимых случайных событий
Событие Обозначим через В дальнейшем мы ограничимся случаем, когда вероятности событий Из определения независимых испытаний вытекает следующий результат: Теорема. Если данные п испытаний независимы, то любые т из них также независимы. Простейшая задача, относящаяся к схеме независимых испытаний, состоит в определении вероятности
Здесь Аi – событие состоящее в том, что событие А произойдет в i- ом испытании. Событие В представляет собой сумму несовместных событий, тогда согласно теореме сложения вероятностей получаем
Вероятность каждого слагаемого в данной сумме по теореме умножения для независимых событий равна
Так как все возможные несовместимые между собой исходы п испытаний состоят в появлении события
Легко заметить, что вероятность Исследуем далее, как ведет себя вероятность при различных значениях m. Поставим теперь более общую задачу. Рассмотрим последовательность n независимых испытаний, в каждом из которых может произойти или не произойти некоторое событие А. При этом вероятность появления события в каждом испытании различна. Обозначим через Следует определить вероятность того что событие А произойдет m раз в серии из n испытаний. Вероятность того, что событие А произойдет m раз в серии из n испытаний равна коэффициенту при
то есть
Обозначим через
В тех случаях когда
Тест Вычисление вероятностей появления события при повторных независимых испытаниях.
1. В каком случае опыты называют независимыми? а) Если вероятности исходов (событий) в каждом из предыдущих опытов не влияют на вероятности этих исходов в последующих опытах б) Если вероятности исходов в каждом из опытов не зависят от порядка следования этих опытов в) Вероятности исходов (событий) в каждом из предыдущих опытов влияют на вероятности этих исходов в последующих опытах
2. Если вероятность появления события в каждом из опытов одинакова, то вероятность появления события m раз при n опытах а) Сначала убывает, затем достигает своего наименьшего значения, а потом увеличивается б) Монотонно убывает в) Сохраняет постоянное значение г) Монотонно возрастает д)Сначала возрастает, затем достигает своего наибольшего значения, а потом уменьшается
3. Если вероятность появления события в каждом из опытов одинакова, то вероятность появления события А m раз при n опытах а) б) в) г)
4. Укажите формулы, по которой можно вычислить вероятность появления события А не менее m раз при n опытах а) б) в)
5. Чему равно наивероятнейшее значение а) Целой части числа б) Максимальному целому числу, большему из в) Целой части числа
6. Если опыты независимы, но вероятности появления события А в каждом из них различны, то вероятность появления события m раз при n опытах а) б) в) Решение типовых задач Пример 7.1. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен): а) три партии из четырех или пять из восьми; б) не менее трех партий из четырех или не менее пяти партий из восьми?
Решение. Так как противники равносильные, то вероятности выигрыша и проигрыша каждой партии одинаковы и равны p = q = l/2. а) Вероятность выиграть три партии из четырех
Вероятность выиграть пять партий из восьми
Так как б) Вероятность выиграть не менее трех партий из четырех
а вероятность выиграть не менее пяти партий из восьми
Так как
Пример 7.2. Имеется шесть потребителей электрического тока, для первого из которых при определенных условиях вероятность того, что произойдет авария, приводящая к отключению потребителя, равна 0,6, для второго — 0,2, а для четырех остальных — по 0,3. Определить вероятность того, что генератор тока будет отключен полностью: а) если все потребители соединены последовательно; б) если потребители соединены так, как показано на схеме (рис. 6).
Решение. а) Вероятность неотключения всех шести потребителей равна произведению вероятностей неотключения каждого потребителя, т. е.
Искомая вероятность равна вероятности отключения хотя бы одного потребителя, т. е. б) В этом случае генератор будет отключен полностью, если в каждой паре последовательно соединенных потребителей отключен хотя бы один потребитель:
Пример 7.3. Большая партия изделий содержит один процент брака. Каков должен быть объем случайной выборки, чтобы вероятность встретить в ней хотя бы одно бракованное изделие была не меньше 0,95?
Решение. Искомое число n находится по формуле В данном случае
Пример 7.4. Оптовая база снабжает 10 магазинов, от каждого из которых может поступить заявка на очередной день с вероятностью 0,4 независимо от заявок других магазинов. Найти наивероятнейшее число заявок в день и вероятность получения этого числа заявок.
Решение. В данном случае n = 10, p = 0,4, (n + 1) p = 4,4. Наивероятнейшеё число Вероятность четырёх заявок из десяти
7.4. Задачи для самостоятельной работы 7.1. Определить вероятность того, что номер первой встретившейся автомашины не содержит: а) цифры пять; б) двух пятерок. Известно, что все номера четырехзначные, неповторяющиеся и равновозможные (считается возможным номер 0000). (Ответ: а) p =
7.2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными 0,5, определить вероятность того, что в данной семье: а) пять мальчиков; б) мальчиков не менее трех, но и не более восьми. (Ответ: а) p =
7.3. В библиотеке имеются книги только по технике и математике. Вероятности того, что любой читатель возьмет книгу по технике и по математике, равны соответственно 0,7 и 0,3. Определить вероятность того, что пять читателей подряд возьмут книги или только по технике, или только по математике, если каждый из них берет только одну книгу. (Ответ: p = 0,17)
7.4. Событие В наступает в том случае, если событие A появится не менее трех раз. Определить вероятность появления события В, если вероятность появления события A при одном опыте равна 0,3 и произведено: а) пять независимых опытов; б) семь независимых опытов. (Ответ: а) p = 0,163; б) р = 0,353)
7.5. Производится четыре независимых опыта, в каждом из которых событие A происходит с вероятностью 0,3. Событие В наступает с вероятностью, равной 1, если событие A произошло не менее двух раз; не может наступить, если событие A не имело места, и наступает с вероятностью 0,6, если событие A имело место один раз. Определить вероятность появления события В. (Ответ: p =
7.6. По мишени в тире произведено 200 независимых выстрелов при одинаковых условиях, которые дали 116 попаданий. Определить, какое значение вероятности попадания на один выстрел более вероятно: (Ответ: Вероятнее первая гипотеза)
7.7. Вероятность хотя бы одного появления события при четырех независимых опытах равна 0,59. Какова вероятность появления события A при одном опыте, если при каждом опыте эта вероятность одинакова? (Ответ: p = 0,2)
7.8. Вероятность появления некоторого события в каждом из восемнадцати независимых опытов равна 0,2. Определить вероятность появления этого события по крайней мере три раза. (Ответ: p = 0,73)
7.9. Игра состоит в набрасывании колец на колышек. Игрок получает 6 колец и бросает кольца до первого попадания. Найти вероятность того, что хотя бы одно кольцо останется неизрасходованным, если вероятность попадания при каждом броске равна 0,1. (Ответ: p =
7.10. Определить вероятность получения не менее 28 очков при трех выстрелах из спортивного пистолета по мишени с максимальным числом очков, равным 10, если вероятность получения 30 очков равна 0,008. Известно, что при одном выстреле вероятность получения восьми очков равна 0,15, а менее восьми очков — 0,4. (Ответ: p =
7.11. Два баскетболиста делают по три броска мячом в корзину. Вероятности попадания мяча при каждом броске равны соответственно 0,6 и 0,7. Найти вероятность того, что: а) у обоих будет равное количество попаданий; б) у первого баскетболиста будет больше попаданий, чем у второго. (Ответ: а) p = 0,321; б) р = 0,243)
7.12. Для прикуривания гражданин пользовался двумя коробками спичек, доставая наудачу ту или иную коробку, Через некоторое время он обнаружил, что одна коробка пуста. Какова вероятность, что во второй коробке при этом k спичек, если вначале в каждой коробке было по n спичек? (Задача Банаха). (Ответ: p =
7.13. Вероятность попадания стрелком в десятку равна 0,7, а в девятку — 0,3. Определить вероятность того, что данный стрелок при трех выстрелах наберет не менее 29 очков. (Ответ: p = 0,784)
7.14. Вероятность возникновения опасной для прибора перегрузки в каждом опыте равна 0,4. Определить вероятность отказа прибора в серии из трех независимых опытов, если вероятности отказа прибора при одной, двух и трех опасных перегрузках соответственно равны 0,2; 0,5 и 0,8. (Ответ: p = 0,2816)
7.15. Вероятность отказа каждого прибора при испытании равна 0,2. Сколько таких приборов нужно испытать, чтобы с вероятностью не менее 0,9 получить не меньше трех отказов? (Ответ: Должно быть
7.16. Охотник стреляет в лося с расстояния 100 м и попадает в него с вероятностью 0,5. Если при первом выстреле попадания нет, то охотник стреляет второй раз, но с расстояния 150 м. Если нет попадания и в этом случае, то охотник стреляет третий раз, причем в момент выстрела расстояние до лося равно 200 м. Считая, что вероятность попадания обратно пропорциональна квадрату расстояния, определить вероятность попадания в лося. (Ответ: p =
7.17. Вероятность попадания в десятку при одном выстреле p = 0,2. Сколько нужно произвести независимых выстрелов, чтобы с вероятностью не менее 0,9 попасть в десятку хотя бы один раз? (Ответ:
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1846; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

 элементарных событий, состоящее из точек
элементарных событий, состоящее из точек  , где
, где  - произвольная точка пространства U, отвечающая испытанию с номером i.
- произвольная точка пространства U, отвечающая испытанию с номером i. , т. е. предположим, что
, т. е. предположим, что
 назовем i-м исходом при s-м испытании. Обозначим вероятность i-го исхода при s-м испытании через
назовем i-м исходом при s-м испытании. Обозначим вероятность i-го исхода при s-м испытании через  .
. событие, состоящее из всех тех точек
событие, состоящее из всех тех точек  пространства
пространства  , для которых
, для которых  . Если в пространстве Un имеет место равенство
. Если в пространстве Un имеет место равенство  при любых
при любых 
 - то испытания называются независимыми.
- то испытания называются независимыми. ; в силу несовместимости и единственной возможности исходов
; в силу несовместимости и единственной возможности исходов  . Эта схема впервые была рассмотрена Я. Бернулли в важнейшем частном случае
. Эта схема впервые была рассмотрена Я. Бернулли в важнейшем частном случае  ; по этой причине указанный случай носит название схемы Бернулли. В схеме Бернулли обычно полагают
; по этой причине указанный случай носит название схемы Бернулли. В схеме Бернулли обычно полагают 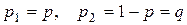 .
. того, что при п испытаниях событие А наступит т раз, а остальные п—т раз наступит противоположное событие
того, что при п испытаниях событие А наступит т раз, а остальные п—т раз наступит противоположное событие  , обозначим это событие В. Тогда
, обозначим это событие В. Тогда
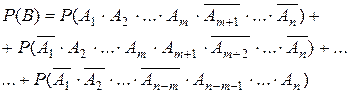
 . По теореме сложения вероятностей искомая вероятность
. По теореме сложения вероятностей искомая вероятность  равна сумме только что вычисленных вероятностей для всех различных способов т появлений события А и n—т не появлений среди п испытаний. Число таких способов, как известно из теории сочетаний, равно
равна сумме только что вычисленных вероятностей для всех различных способов т появлений события А и n—т не появлений среди п испытаний. Число таких способов, как известно из теории сочетаний, равно 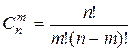 ; следовательно, искомая вероятность равна
; следовательно, искомая вероятность равна
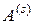 0 раз, 1 раз, 2 раза,..., n раз, то ясно, что
0 раз, 1 раз, 2 раза,..., n раз, то ясно, что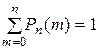
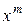 в разложении бинома
в разложении бинома  по степеням x.
по степеням x.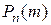 с увеличением m сначала возрастает, затем достигает максимума и при дальнейшем росте m убывает. При этом, если
с увеличением m сначала возрастает, затем достигает максимума и при дальнейшем росте m убывает. При этом, если  является целым числом, то максимальное значение вероятность
является целым числом, то максимальное значение вероятность  принимает для двух значений m, а именно
принимает для двух значений m, а именно  и
и 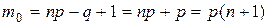 . Если же
. Если же  , равном максимальному целому числу, большему из
, равном максимальному целому числу, большему из  и
и 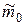 . Число
. Число  .
.
 . Аi – событие состоящее том что А произойдет в i-ом испытании
. Аi – событие состоящее том что А произойдет в i-ом испытании  – событие состоящее том что А не произойдет в i-ом испытании соответственно.
– событие состоящее том что А не произойдет в i-ом испытании соответственно. в выражении производящей функции
в выражении производящей функции


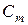 событие состоящее в том, что А появляется не менее m раз в n независимых испытаниях, а вероятность
событие состоящее в том, что А появляется не менее m раз в n независимых испытаниях, а вероятность  обозначим
обозначим  , тогда
, тогда
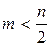 удобно пользоваться следующей формулой
удобно пользоваться следующей формулой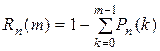







 и
и 
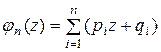


 .
. , то вероятнее выиграть три партии из четырех.
, то вероятнее выиграть три партии из четырех. ,
, .
.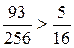 , то вероятнее выиграть не менее пяти партий из восьми.
, то вероятнее выиграть не менее пяти партий из восьми.
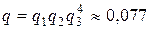 .
. .
. .
.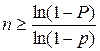 .
. , а
, а  . Поэтому
. Поэтому  .
. .
. ; б) р =
; б) р =  )
) б) р =
б) р =  )
) )
)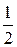 или
или  , если до опыта обе гипотезы равновероятны и единственно возможны.
, если до опыта обе гипотезы равновероятны и единственно возможны. )
) )
) )
) )
) )
) )
)


