
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условная вероятность и простейшие основные формулы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Мы уже говорили, что в основе определения вероятности события лежит некоторая совокупность условий. Если никаких ограничений, кроме условий, при вычислении вероятности Однако в ряде случаев приходится находить вероятности событий при дополнительном условии, что произошло некоторое событие В, имеющее не нулевую вероятность, т.е Пример 1. Брошены две игральные кости. Чему равна вероятность того, что сумма выпавших на них очков равна 8 (событие A), если известно, что эта сумма есть четное число (событие В)? Все возможные случаи, которые могут представиться при бросании двух костей, мы запишем в таблице 1.7.1, каждая клетка которой содержит запись возможного события: на первом месте в скобках указывается число очков, выпавших на первой кости, на втором месте — число очков, выпавших на второй кости. Табл. 1.7.1
Общее число возможных случаев — 36, благоприятствующих событию A — 5. Таким образом, безусловная вероятность Если событие В произошло, то осуществилась одна из 18 (а не 36) возможностей и, следовательно, условная вероятность равна Пример 2. Из колоды карт последовательно вынуты две карты. Найти: а) безусловную вероятность того, что вторая карта окажется тузом (неизвестно, какая карта была вынута вначале), и б) условную вероятность, что вторая карта будет тузом, если первоначально был вынут туз. Обозначим через A событие, состоящее в появлении туза на втором месте, а через В —событие, состоящее в появлении туза на первом месте. Ясно, что имеет место равенство В силу несовместимости событий АВ и АВ имеем: При вынимании двух карт из колоды в 36 карт могут произойти 36•35 (учитывая порядок!) случаев. Из них благоприятствующих событию АВ — 4•3 случаев, а событию Если первая карта есть туз, то в колоде осталось 35 карт и среди них только три туза. Следовательно, Общее решение задачи нахождения условной вероятности для классического определения вероятности не представляет труда. В самом деле, пусть из n единственно возможных, несовместимых и равновероятных событий
Точно так же можно вывести, что
Понятно, что
т. е. вероятность произведения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого при условии, что первое произошло. Теорема умножения применима и в том случае, когда одно из событий А или В есть невозможное событие, так как в этом случае вместе с Условная вероятность обладает всеми свойствами вероятности. В этом легко убедиться, проверив, что она удовлетворяет всем свойствам, сформулированных в предыдущих параграфах. Действительно, первое свойство выполняется очевидным образом, поскольку для каждого события А определена неотрицательная функция Проверка третьего свойства также не составляет труда и мы предоставляем читателю ее осуществление. Заметим, что вероятностное пространство для условных вероятностей задается следующей тройкой Определение 1. Говорят, что событие А независимо от события В, если имеет место равенство Если событие А независимо от В, то имеет место равенство Если события А и В независимы, то независимы также события А и Отсюда мы делаем важное заключение: если события А и В независимы, то независимы также каждые два события Понятие независимости событий играет значительную роль в теории вероятностей и в ее приложениях. В частности, большая часть результатов, изложенных в настоящем пособии, получена в предположении независимости тех или иных рассматриваемых событий. Так, например, ясно, что выпадение герба на одной монете не изменяет вероятности появления герба (решки) на другой монете, если только эти монеты во время бросания не связаны между собой (например, жестко не скреплены). Точно так же рождение мальчика у одной матери не изменяет вероятности появления мальчика (девочки) у другой матери. Это — события независимые. Для независимых событий теорема умножения принимает особенно простой вид, а именно, если события A и В независимы, то Мы обобщим теперь понятие независимости двух событий на совокупность нескольких событий. Определение 2. События Заметим, что для независимости в совокупности нескольких событий недостаточно их по парной независимости. В этом можно убедиться на следующем простом примере. Пример С.Н. Бернштейна. Представим себе, что грани тетраэдра окрашены: 1-я — в красный цвет (A), 2-я — в зеленый (В), третья — в синий (С) и 4-я — во все эти три цвета (AВС). Легко видеть, что вероятность выпадения грани, на которую упадет тетраэдр при бросании, и своей окраске иметь красный цвет равна 1/2: граней четыре и две из них имеют в окраске красный цвет. Таким образом, Однако, если нам известно, что осуществились события В и С, то заведомо осуществилось и событие A, т. е. Таким образом, события A,В,С в совокупности зависимы. Таким образом, в общем случае при (В случае Формула полной вероятности. Предположим теперь, что событие В может осуществиться с одним и только с одним из n несовместимых событий Применяя теорему умножения, находим:
Это равенство носит название формулы полной вероятности и играет важную роль во всей дальнейшей теории. В качестве иллюстрации рассмотрим два примера. Пример 1. Имеется пять урн: 2 урны состава A1 — по два белых шара и одному черному, 1 урна состава A2 —по 10 черных шаров, 2 урны состава A3 — по три белых шара и одному черному. Наудачу выбирается урна и из нее наудачу вынимается шар. Чему равна вероятность, что вынутый шар белый (событие В)? Так как вынутый шар может быть только из урны 1-го, 2-го или 3-го состава, то По формуле полной вероятности
Но
Таким образом, Пример 2. Известно, что вероятность поступления k вызовов на телефонную станцию за промежуток времени t равна Считая, что появление какого-либо числа вызовов за два соседних промежутка времени являются событиями независимыми, найти вероятность поступления s вызовов за промежуток времени длительности 2 t. Решение. Обозначим через По теореме сложения вероятностей
По теореме умножения вероятностей для независимых событий
Таким образом, если положить Впоследствии мы увидим, что при некоторых весьма общих условиях находим:
Но
Поэтому
Для промежутков времени, в два раза больших, и, как легко убедиться, для любых кратных t промежутков времени характер формулы для вероятности сохраняется. Формула Бейеса. Получим важные формулы Бейеса или, как иногда говорят, формулы вероятности гипотез. Требуется найти вероятность события Ai, если известно, что В произошло. Согласно теореме умножения имеем:
Из соотношения (1.9.1) получаем
используя формулу полной вероятности (1.8.1), находим:
Полученные формулы (1.9.3) носят название формул Бейеса. Общая схема применения этих формул к решению практических задач такова. Пусть событие В может протекать в различных условиях, относительно характера которых может быть сделано n гипотез: Вероятности Пример 1. Имеется пять урн следующего состава: 2 урны (состава 2 урны (состава 1 урна (состава Из одной наудачу выбранной урны взят шар. Он оказался белым (событие В). Чему равна после опыта вероятность (апостериорная вероятность) того, что шар вынут из урны третьего состава? Согласно предположению
Согласно формуле Бейеса имеем:
Точно так же находим:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 725; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.73.149 (0.016 с.) |

 не налагается, то такие вероятности называются безусловными.
не налагается, то такие вероятности называются безусловными. . Данные вероятности мы будем называть условными и обозначать символом
. Данные вероятности мы будем называть условными и обозначать символом  ; это означает вероятность события А при условии, что событие В произошло.
; это означает вероятность события А при условии, что событие В произошло. .
. .
. .
. .
. — 32 • 4 случаев. Таким образом,
— 32 • 4 случаев. Таким образом, 
 .
. событию А благоприятствует m событий. Если событие В произошло, то это означает, что наступило одно из событий
событию А благоприятствует m событий. Если событие В произошло, то это означает, что наступило одно из событий 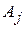 , благоприятствующих В. При этом условии событию А благоприятствуют r и только r событий Aj, благоприятствующих АВ. Таким образом,
, благоприятствующих В. При этом условии событию А благоприятствуют r и только r событий Aj, благоприятствующих АВ. Таким образом,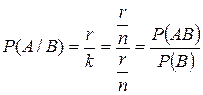
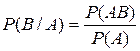

 имеют место равенства
имеют место равенства  и
и  .
. , то
, то  .
. .
. т. е. если наступление события В не изменяет вероятности появления события А.
т. е. если наступление события В не изменяет вероятности появления события А. . Отсюда находим:
. Отсюда находим:  т. е. событие В также независимо от А. Таким образом, свойство независимости событий взаимно.
т. е. событие В также независимо от А. Таким образом, свойство независимости событий взаимно.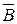 . Действительно, так как
. Действительно, так как  и по предположению
и по предположению  .
. .
. .
. называются независимыми в совокупности, если для любого события
называются независимыми в совокупности, если для любого события  из их числа и произвольных
из их числа и произвольных  из их же числа события
из их же числа события  взаимно независимы. В силу предыдущего это определение эквивалентно: при любых
взаимно независимы. В силу предыдущего это определение эквивалентно: при любых  и
и 
 .
. . Точно так же можно подсчитать, что
. Точно так же можно подсчитать, что  события A,В,С, таким образом, попарно независимы.
события A,В,С, таким образом, попарно независимы. .
. по определению
по определению  .
.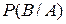 остается неопределенной.) Это позволяет нам перенести автоматически на общее понятие вероятности все определения и результаты настоящего параграфа.
остается неопределенной.) Это позволяет нам перенести автоматически на общее понятие вероятности все определения и результаты настоящего параграфа. , где события BAi и BAj с разными индексами i и j несовместимы. По теореме сложения вероятностей имеем:
, где события BAi и BAj с разными индексами i и j несовместимы. По теореме сложения вероятностей имеем:  .
.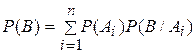
 .
.

 .
. .
.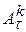 событие, состоящее в поступлении k вызовов за время
событие, состоящее в поступлении k вызовов за время  . Очевидно, что мы имеем следующее равенство:
. Очевидно, что мы имеем следующее равенство:  , которое означает, что событие
, которое означает, что событие 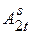 можно рассматривать как сумму s+ 1 несовместимых событий, состоящих в том, что за первый промежуток времени длительности t поступает i вызовов, а за следующий промежуток той же продолжительности — поступает s — i вызовов
можно рассматривать как сумму s+ 1 несовместимых событий, состоящих в том, что за первый промежуток времени длительности t поступает i вызовов, а за следующий промежуток той же продолжительности — поступает s — i вызовов  .
.

 , то
, то  .
. .
.  , где а — некоторая константа.
, где а — некоторая константа.





 этих гипотез до испытания(априорные вероятности гипотез). Известно также, что гипотеза
этих гипотез до испытания(априорные вероятности гипотез). Известно также, что гипотеза  сообщает событию В вероятность
сообщает событию В вероятность  . Произведен опыт, в котором событие В наступило. Это должно вызвать переоценку вероятностей гипотез
. Произведен опыт, в котором событие В наступило. Это должно вызвать переоценку вероятностей гипотез  называются апостериорными вероятностями события
называются апостериорными вероятностями события  ) по 2 белых и 3 черных шара,
) по 2 белых и 3 черных шара, ) по 1 белому и 4 черных шара,
) по 1 белому и 4 черных шара,





