
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие случайной величины и функции распределения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Одним из основных понятий теории вероятностей является понятие случайной величины. Прежде чем переходить к формальному его определению, мы остановимся на рассмотрении примеров. Пример 1. Число космических частиц, попадающих на определенный участок земной поверхности в течение промежутка времени определенной длины, подвержено значительным колебаниям в зависимости от многих случайных обстоятельств. Пример 2. Размер уклонения точки падения снаряда от центра цели определяется большим количеством разнообразных причин, носящих случайный характер. В результате в теории стрельбы вынуждены считаться с явлением рассеивания снарядов около центра цели как со случайным явлением и рассматривать указанные уклонения как случайные величины. Пример 3. Скорость молекулы газа не остается неизменной, а меняется в зависимости от столкновений с другими молекулами. Этих столкновений очень много даже в течение короткого промежутка времени. Зная скорость молекулы в данный момент, нельзя с полной определенностью указать ее значение, скажем, через 0,01 или 0,001 секунды. Изменение скорости молекулы носит случайный характер. Приведенные примеры показывают с достаточной определенностью, что со случайными величинами приходится иметь дело в самых разнообразных областях науки и техники. Несмотря на всю разнородность конкретного содержания приведенных нами примеров, все они с точки зрения математики представляют одну и ту же картину. А именно, в каждом примере мы имеем дело с величиной, так или иначе характеризующей исследуемое явление. Каждая из этих величин под влиянием случайных обстоятельств способна принимать различные значения. Заранее указать, какое значение примет эта величина, нельзя, так как оно меняется случайным образом от испытания к испытанию. Разнообразие случайных величин весьма велико. Число принимаемых ими значений может быть конечным, счетным и несчетным; значения могут быть расположены дискретно или заполнять интервалы сплошь, или же не заполнять интервалы, но располагаться всюду плотно. Для того чтобы задавать вероятности значений случайных величин, столь различных по своей природе, и притом задавать их одним и тем же способом, в теории вероятностей вводят понятие функции распределения случайной величины. Рассмотрим пример с подбрасыванием игральной кости: Выпадению одного и двух очков сопоставим число –1 и будем считать, что это проигрыш; Выпадению трех и четырех очков сопоставим число 0 и будем считать, что это ничья; Выпадению пяти и шести очков сопоставим число +1 и будем считать, что это выигрыш; Множество элементарных исходов в данном случае будет
Аргументом это функции является случайное событие. При определении случайной величины будем исходить в соответствии с общими понятиями случайного события из множества элементарных событий U, поля событий F определенной на нем вероятности P(A). Пусть задано вероятностное пространство { U, F, P }. Определение 1. Случайной величиной называется вещественная функция X (u), определенная на элементах пространства элементарных событий U, так что
Иначе можно считать, что X (u) есть случайная величина, если для любого события Пусть X — случайная величина и х — произвольное действительное число. Вероятность того, что X, примет значение, меньшее чем х будет зависеть от значений x. Таким образом вероятность события
Условимся в дальнейшем, как правило, случайные величины обозначать прописными латинскими буквами, а принимаемые ими значения — строчными. Резюмируем сказанное, случайной величиной называется переменная величина, значения которой зависят от случая и для которой определена функция распределения вероятностей. Пример 1. Мы скажем, что случайная величина нормально распределена, если ее функция распределения имеет вид
где С > 0,
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 612; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

 . В соответствии с принятыми правилами на множестве элементарных исходов определена функция
. В соответствии с принятыми правилами на множестве элементарных исходов определена функция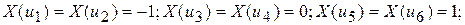
 - числовой оси, множество U1 на которых функция X (u) строго меньше x является элементом поля событий F, то есть
- числовой оси, множество U1 на которых функция X (u) строго меньше x является элементом поля событий F, то есть
 определена вероятность
определена вероятность  . Часто аргумент функции X (u) можно опускать, то есть
. Часто аргумент функции X (u) можно опускать, то есть 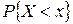 .
.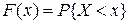

 > 0, m — постоянные. Впоследствии мы установим связь между постоянными
> 0, m — постоянные. Впоследствии мы установим связь между постоянными 


