
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие 4. Теорема сложения вероятностей.Содержание книги
Поиск на нашем сайте
Краткая теоретическая часть Вероятность суммы двух событий определяется по формуле P(A + В) = Р(A)+Р(B) — Р(AB), которая обобщается на сумму любого числа событий
Для несовместных событий вероятность суммы событий равна сумме вероятностей этих событий, т. е. Тест 1. В каком случае события А и В называются несовместными или несовместимыми? а) Когда вероятность появления одного из них не зависит от вероятности появления второго б) Когда хотя бы одно из этих событий произойдет в ходе испытания в) Когда совместное появление этих событий невозможно г) Когда оба этих события произойдут в ходе опыта
2. Укажите события, которые являются совместимыми. а) Выпадение «герба» и цифры при подбрасывании монеты б) Присутствие одного и того же студента одновременно на лекции в аудитории и в кинотеатре в) Наступление весны по календарю и выпадение снега г) Появление на выпавшей грани каждой из двух игральных костей трех очков и равенство суммы очков на выпавших гранях обеих костей нечетному числу д) Показ по одному каналу телевидения футбольного матча, а по другому – выпуска новостей
3. Теорема сложения вероятностей несовместных событий формулируется следующим образом: а) Вероятность появления одного из двух несовместных событий равна вероятности появления второго события б) Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий в) Вероятность появления одного из двух несовместных событий равна разности вероятностей появления этих событий
4. Теорема сложения вероятностей совместных событий формулируется следующим образом: а) Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий б) Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления в) Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий и вероятности их совместного появления
5. Теорема сложения вероятностей обобщается на сумму любого числа событий и вероятность суммы событий в общем виде вычисляется по формуле: а) б) в)
6. Если события а) б)
в) Решение типовых задач Пример 4.1. Определить вероятность того, что партия из ста изделий, среди которых пять бракованных, будет принята при испытании наудачу выбранной половины всей партии, если условиями приема допускается бракованных изделий не более одного из пятидесяти.
Решение. Введем в рассмотрение событие С, состоящее в том, что партия из ста изделий, среди которых пять бракованных, будет принята при испытании наудачу выбранной половины всей партии. Обозначим через А событие, состоящее в том, что при испытании не получено ни одного бракованного изделия, а через В — событие, состоящее в том, что получено только одно бракованное изделие. Так как С=А+В, то искомая вероятность P(C) = Р(А + B). События А и В несовместны. Поэтому P(C) = Р(А)+ Р(B). Из 100 изделий 50 можно выбрать Поэтому Р(A)= Аналогично Р(B)= Тогда P(C) = Р(А)+ Р(B)=
Пример 4.2. Электрическая цепь между точками М и N составлена по схеме, приведенной на рис. 5.
Таблица 1
Определить вероятность разрыва цепи за указанный промежуток времени.
Решение.
Введем в рассмотрение событие С, состоящее в том, что за указанный промежуток времени будет разрыв цепи. Обозначим через Aj (j = 1,2) событие, состоящее в выходе из строя элемента Кj, через А — выход из строя хотя бы одного элемента Кj, а через В — выход из строя всех трех элементов Аi (i =1, 2, 3). Тогда искомая вероятность Р(С) = Р(A + В) = Р(A) + Р(В) — Р(A)Р(B). Так как Р(A) = Р(A1) + Р(A2) — Р(A1)Р(A2) = 0,8, Р(В) = Р(Л1)Р(Л 2) Р(Л3) = 0,252, то Пример 4.3. В урне имеются n белых, m черных и l красных шаров, которые извлекаются наудачу по одному: а) без возвращения; б) с возвращением после каждого извлечения. Определить в обоих случаях вероятности того, что белый шар будет извлечен раньше черного.
Решение. Пусть Р1 — вероятность того, что белый шар будет извлечен раньше черного, а Р11 — вероятность того, что черный шар будет извлечен раньше белого. Вероятность Р1 является суммой вероятностей извлечения белого шара сразу, после извлечения одного красного, двух красных и т. д. Таким образом, можно записать в случае, когда шары не возвращаются,
а при возвращении шаров
Для получения вероятностей Р11 в предыдущих формулах нужно произвести замену n на m, а m на n. Отсюда следует, что в обоих случаях Р1: Р11 = n: m. Так как, кроме того, Р1 + Р11 = 1, то искомая вероятность при извлечении шаров без возвращения также равна Пример 4.4. Некто написал n писем, запечатал их в конверты, а затем наудачу на каждом из них написал различные адреса. Определить вероятность того, что хотя бы на одном из конвертов написан правильный адрес.
Решение. Пусть событие Ak состоит в том, что на k -м конверте написан правильный адрес (k = l, 2,..., n). Искомая вероятность События Ak совместны; при любых различных k, j, i,... имеют место равенства:
Используя формулу для вероятности суммы n событий, получаем
или
При больших n 4.4. Задачи для самостоятельной работы 4.1. Каждое из четырех несовместных событий может произойти соответственно с вероятностями 0,012, 0,010, 0,006 и 0,002. Определить вероятность того, что в результате опыта произойдет хотя бы одно из этих событий. (Ответ: p = 0,03)
4.2. Стрелок производит один выстрел в мишень, состоящую из центрального круга и двух концентрических колец. Вероятности попадания в круг и кольца соответственно равны 0,20, 0,15 и 0,10. Определить вероятность непопадания в мишень. (Ответ: p = 0,55)
4.3. Две одинаковые монеты радиуса r расположены внутри круга радиуса R, в который наудачу бросается точка. Определить вероятность того, что эта точка упадет на одну из монет, если монеты не перекрываются. (Ответ: p =
4.4. Какова вероятность извлечь из колоды в 52 карты фигуру любой масти или карту пиковой масти (фигурой называется валет, дама или король)? (Ответ: p =
4.5. В ящике имеются 10 монет по 20 коп., 5 монет по 15 коп. и 2 монеты по 10 коп. Наугад берутся шесть монет. Какова вероятность, что в сумме они составят не более одного рубля? (Ответ: p =
4.6. В двух урнах находятся шары, отличающиеся только цветом, причем в первой урне 5 белых шаров, 11 черных и 8 красных, а во второй соответственно 10, 8 и 6. Из обеих урн наудачу извлекается по одному шару. Какова вероятность, что оба шара одного цвета? (Ответ: p = 0,323)
4.7. Игра между A и B ведется на следующих условиях: в результате первого хода, который всегда делает А, он может выиграть с вероятностью 0,3; если первым ходом A не выигрывает, то ход делает В и может выиграть с вероятностью 0,5; если в результате этого хода В не выигрывает, то A делает второй ход, который может привести к его выигрышу с вероятностью 0,4. Определить вероятности выигрыша для А и для В. (Ответ:
4.8. Вероятность для данного спортсмена улучшить свой предыдущий результат с одной попытки равна р. Определить вероятность того, что на соревнованиях спортсмен улучшит свой результат, если разрешается делать две попытки. (Ответ: p(А) =
4.9. Из урны, содержащей n шаров с номерами от 1 до n, последовательно извлекаются два шара, причем первый шар возвращается, если его номер не равен единице. Определить вероятность того, что шар с номером 2 будет извлечен при втором извлечении. (Ответ: p =
4.10. Игрок А поочередно играет с игроками В и С, имея вероятность выигрыша в каждой партии 0,25, и прекращает игру после первого проигрыша или после двух партий, сыгранных с каждым игроком. Определить вероятности выигрыша В и С. (Ответ:
4.11. Двое поочередно бросают монету. Выигрывает тот, у которого раньше появится герб. Определить вероятности выигрыша для каждого из игроков. (Ответ:
4.12. Вероятность получить очко, не теряя подачи, при игре двух равносильных волейбольных команд равна половине. Определить вероятность получения одного очка для подающей команды. (Ответ: p =
4.13. Два стрелка поочередно стреляют по мишени до первого попадания. Вероятность попадания для первого стрелка равна 0,2, а для второго равна 0,3. Найти вероятность того, что первый стрелок сделает больше выстрелов, чем второй. (Ответ: p = 0,455)
4.14. Двое играют до победы, причем для этого необходимо первому выиграть т партий, а второму п партий. Вероятность выигрыша каждой партии первым игроком равна р, а вторым q =1— р. Определить вероятность выигрыша всей игры первым игроком. (Ответ: p(A) =
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1945; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.244 (0.006 с.) |

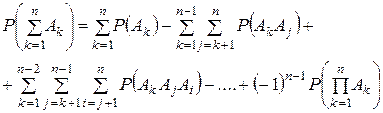
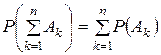 .
.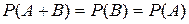

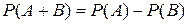
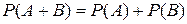
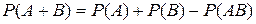
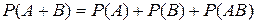


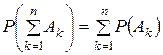
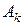 ,
, 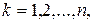 являются несовместными, то вероятность суммы этих событий равна:
являются несовместными, то вероятность суммы этих событий равна:

 способами. Из 95 небракованных изделий 50 можно выбрать
способами. Из 95 небракованных изделий 50 можно выбрать 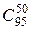 способами.
способами.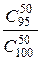 .
.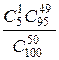 .
.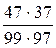 =0,181.
=0,181. Выход из строя за время Т различных элементов цепи — независимые события, имеющие следующие вероятности (табл. 1).
Выход из строя за время Т различных элементов цепи — независимые события, имеющие следующие вероятности (табл. 1).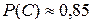 .
.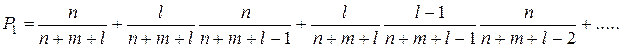

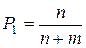 .
.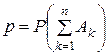 .
.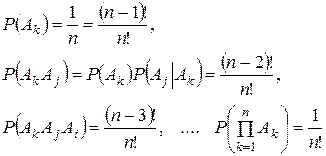

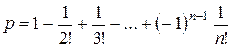
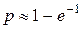 .
. )
)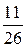 )
)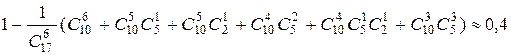 )
)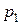 = 0,44,
= 0,44,  = 0,35)
= 0,35)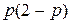 )
) )
)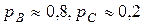 )
) )
) )
) )
)


