
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение и простейшие свойства характеристических функций.Содержание книги
Поиск на нашем сайте Определение 1. Характеристической функцией
если X – дискретная случайная величина и известен ряд ее распределения, то
если X – непрерывная случайная величина с известной плотностью распределения f(x), то
Следует заметить, что ряд (8.1.2) и интеграл (8.1.3) сходится абсолютно. Рассмотрим сходимость на примере интеграла (8.1.3)
Теорема 1. Характеристическая функция равномерно непрерывна на всей прямой и удовлетворяет следующим соотношениям:
Доказательство. Соотношения (8.1.4) немедленно вытекают из определения характеристической функции. Действительно, подставляя в (8.1.3)
Откуда Нам остается доказать равномерную непрерывность функции q(x). С этой целью рассмотрим разность
и оценим ее по модулю. Имеем:
Пусть
и подберем столь малое h, чтобы для
Тогда, учитывая (8.1.6) и (8.1.7) получаем
Это неравенство доказывает теорему. Теорема 2. Если
где Доказательство. Действительно,
Теорема 3. Характеристическая функция суммы двух независимых случайных величин равна произведению их характеристических функций. Доказательство. Пусть X и Y — независимые случайные величины и Это доказывает теорему. Следствие. Если
причем каждое слагаемое независимо от суммы предыдущих, то характеристическая функция величины X равна произведению характеристических функций слагаемых. Применение характеристических функций в значительной степени опирается на свойство, сформулированное в теореме 3. Сложение независимых случайных величин приводит к весьма сложной операции — композиции функций распределения слагаемых. Для характеристических функций эта сложная операция заменяется весьма простой — простым умножением характеристических функций. Теорема 4(единственности). Распределения F(x),f(x) однозначно определяются своей характеристической функцией Обратное соответствие устанавливается, в частности, следующей формулой:
Теорема 5(непрерывности). а) Если последовательность функций распределения б) Если последовательность характеристических функций Теорема 6. Если случайная величина X имеет абсолютный момент п-го порядка, то характеристическая функция величины X дифференцируема п раз и при
Доказательство. Действительно, k - кратное (
Но
и, следовательно, в силу предположения теоремы ограничен. Отсюда следует существование интеграла (8.1.12) и законность дифференцирования. Положив в (8.1.12) t= 0, получим:
Математическое ожидание и дисперсия весьма просто выражаются при помощи производных от логарифма характеристической функции. В самом деле, положим
Приняв во внимание, что qx (0)=1 и равенство (8.1.11), находим:
Отсюда
Производная k -го порядка логарифма характеристической функции в точке 0, умноженная на Как это непосредственно следует из теоремы 3, при сложении независимых случайных величин их семиинварианты складываются. Мы только что видели, что первыми двумя семиинвариантами являются математическое ожидание и дисперсия, т. е. момент первого порядка и некоторая рациональная функция моментов первого и второго порядков. Путем вычислений легко убедиться, что семиинвариант любого порядка k есть (целая) рациональная функция первых k моментов. Для примера приведем явные выражения семиинвариантов третьего и четвертого порядков:
Рассмотрим теперь несколько примеров характеристических функций. Пример 1. Случайная величина X распределена по нормальному закону с математическим ожиданием а и дисперсией
Подстановкой
Известно, что при любом вещественном a
следовательно.
В частном случае, когда Пример 2. Найти характеристическую функцию случайной величины X, распределенной по закону Пуассона. Согласно предположению, случайная величина X принимает только целочисленные значения, причем
где
отсюда находим:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 661; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |

 случайной величины X называется математическое ожидание случайной величины
случайной величины X называется математическое ожидание случайной величины  , то есть
, то есть




 получим
получим 

 .
.

 произвольно; выберем столь большое А, чтобы
произвольно; выберем столь большое А, чтобы
 выполнилось условие
выполнилось условие

 , где a и b — постоянные, то
, где a и b — постоянные, то
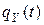 и
и  есть характеристические функции величин Y и X.
есть характеристические функции величин Y и X.
 . Так как X и Y независимы, то случайные величины
. Так как X и Y независимы, то случайные величины  и
и  . Отсюда вытекает, что
. Отсюда вытекает, что  .
.
 .
.
 сходится к функции распределения F в точках ее непрерывности, то последовательность
сходится к функции распределения F в точках ее непрерывности, то последовательность  соответствующих характеристических функций сходится к характеристической функции
соответствующих характеристических функций сходится к характеристической функции  распределения F.
распределения F. сходится всюду на R1 к некоторой функции
сходится всюду на R1 к некоторой функции  , непрерывной в точке t =0, то
, непрерывной в точке t =0, то 

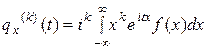


 . Тогда
. Тогда




 , называется семиинвариантом k-го порядка случайной величины.
, называется семиинвариантом k-го порядка случайной величины.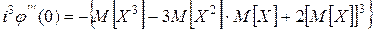

 . Характеристическая функция величины равна
. Характеристическая функция величины равна

 приводится к виду
приводится к виду


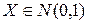 , то есть a =0, а
, то есть a =0, а  =1, то характеристическая функция имеет вид
=1, то характеристическая функция имеет вид  .
.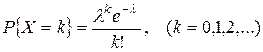
 — постоянная. Характеристическая функция величины X равна
— постоянная. Характеристическая функция величины X равна




