
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие 10. Дискретные и непрерывные случайные величины.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Краткая теоретическая часть Математическое ожидание
Математические ожидания и дисперсии непрерывных случайных величин обладают такими же свойствами, что и аналогичные вероятностные характеристики дискретных случайных величин. Среднее квадратическое отклонение
Для симметричного закона распределения характеристикой рассеивания случайной величины может служить срединное отклонение Е, определяемое из условия
Начальный момент k -ro порядка mk и центральный момент k -ro порядка
Для существования моментов нечетного порядка необходима абсолютная сходимость соответствующих интегралов.
Тест 1. Выберите те из следующих предложений, которые являются верными. Математическое ожидание и дисперсия непрерывных случайных величин… а) являются вероятностными характеристиками, не имеющими ничего общего с аналогичными характеристиками дискретных случайных величин б) обладают такими же свойствами, что и аналогичные вероятностные характеристики дискретных случайных величин в) как и в случае дискретных случайных величин, определяют положение реализации случайной величины на числовой прямой и рассеянье случайной величины соответственно 2. Математическое ожидание а)
б)
в)
г)
3. Начальный а) дискретных случайных величин б) непрерывных случайных величин в) и дискретных, и непрерывных случайных величин
4. Начальный а)
где б)
где в)
где г)
где
Решение типовых задач Пример 10.1. Плотность вероятности случайных амплитуд боковой качки корабля имеет вид (закон Рэлея)
Определить: а) математическое ожидание М[X]; б) дисперсию D[Х] и среднее квадратическое отклонение в) центральные моменты третьего и четвертого порядков Решение. Вычисление моментов сводится к вычислению интегралов вида
которые равны: при n четном
где
и при n нечетном
Математическое ожидание случайной амплитуды боковой качки равно
Произведя замену переменных
б) Так как
в) где Следовательно,
Следовательно, Пример 10.2. Найти срединное отклонение случайной величины, плотность вероятности которой имеет вид (распределение Лапласа)
Решение. Так как плотность вероятности симметрична относительно нуля, то
Отсюда 10.4. Задачи для самостоятельной работы
10.1. Плотность вероятности случайной величины Х имеет вид (закон равномерного распределения)
Определить: а) б) в) найти связь между средним квадратическим и срединным отклонениями случайной величины Х. (Ответ: а)
10.2. Функция распределения случайной величины Х имеет вид (закон арксинуса)
Определить постоянные a и b. Найти (Ответ:
10.3. Определить математическое ожидание и дисперсию случайной величины Х, если плотность вероятности
(Ответ:
10.4. Плотность вероятности случайной величины Х имеет вид (закон арксинуса)
Определить дисперсию и срединное отклонение. (Ответ:
10.5. Плотность вероятности случайных амплитуд А боковой качки корабля определяется формулой (закон Рэлея)
где Одинаково ли часто встречаются амплитуды, меньшие и большие средней? (Ответ: 10.6. Скорость молекул газа имеет плотность вероятности (закон Максвелла)
Найти математическое ожидание и дисперсию скорости молекул, а также величину А при заданном h. (Ответ:
10.7. Плотность вероятности случайной величины X задана в виде
Определить (Ответ:
10.8. Функция распределения случайной величины X имеет вид
Найти М[Х] и D[X]. (Ответ: 10.9. Найти математическое ожидание и дисперсию случайной величины, плотность вероятности которой имеет вид (распределение Лапласа):
(Ответ:
10.10. Случайная величина X имеет плотность вероятности (гамма-распределение)
Определить параметр А, математическое ожидание и дисперсию случайной величины X. (Ответ:
10.11. Случайная величина X имеет плотность вероятности (бета-распределение)
Определить параметр А, математическое ожидание и дисперсию случайной величины X. (Ответ: 10.12. Случайная величина X имеет плотность вероятности
где (Ответ: Указание: Для вычисления интеграла 10.13. Плотность вероятности неотрицательной случайной величины X имеет вид (
где Определить А, математическое ожидание и дисперсию случайной величины X. (Ответ:
10.14. Доказать, что при выполнении условий
для математического ожидания случайной величины справедливо равенство
(Указание: Воспользоваться соотношением
10.15. Вероятность обнаружения затонувшего судна за время поиска t задается формулой
Определить среднее время поиска, необходимое для обнаружения судна. (Ответ: Указание: Обратить внимание на то, что
10.16. Определить математическое ожидание m(t) массы радиоактивного вещества спустя время t, если в начальный момент масса вещества была (Ответ: Указание: Учесть, что вероятность распада любого фиксированного атома за промежуток времени
10.17. Определить время полураспада радиоактивного вещества, если вероятность распада ядра любого атома в единицу времени постоянна и равна р. (Время полураспада Тп определяется моментом, когда масса радиоактивного вещества в среднем уменьшается вдвое.) (Ответ: Указание: Воспользоваться решением задачи 10.16)
10.18. Обработка результатов одной переписи показала, что плотность вероятности возраста лиц, занимающихся научной работой, может быть представлена формулой
Определить, во сколько раз число научных работников в возрасте ниже среднего превышает число научных работников в возрасте выше среднего. (Ответ:
10.19. Найти для распределения Стьюдента, задаваемого плотностью вероятности
начальные моменты при (Ответ: Указание: При вычислении интегралов вида
10.20. Случайная величина X подчиняется бета-распределению, т. е. имеет плотность вероятности
Найти начальный момент k -гoпорядка. (Ответ:
10.21. Найти математическое ожидание и дисперсию случайной величины, имеющей в интервале (Ответ:
10.22. Выразить центральный момент (Ответ: 10.23. Выразить начальный момент (Ответ:
Занятие 11. Закон Пуассона. Краткая теоретическая часть Законом распределения Пуассона называется ряд распределения случайной величины X вида
где Законом Пуассона может быть приближенно заменено биномиальное распределение, когда вероятность р появления события А в каждом отдельном опыте мала, а число п производимых опытов велико. В этом случае имеет место приближенное равенство
где
Тест 1. Распределенными по закону Пуассона могут быть: а) только дискретные случайные величины б) только непрерывные случайные величины в) и дискретные, и непрерывные случайные величины
2. Является ли обязательным условие, что случайная величина может быть распределенной по закону Пуассона только в случае, если она принимает целочисленные значения? а) Да б) Нет
3. Законом распределения Пуассона называется ряд распределения случайной величины а) б) в) г) д)
4. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, обладают следующим свойством: а) равны нулю б) равны между собой в) равны параметру Пуассона
Решение типовых задач Пример 11.1. Радиоаппаратура состоит из 1000 электроэлементов. Вероятность отказа одного элемента в течение одного года работы равна 0,001 и не зависит от состояния других элементов. Какова вероятность отказа двух и не менее двух электроэлементов за год? Решение. Считая случайное число X отказавших элементов подчиняющимся закону Пуассона
1) вероятность отказа ровно двух элементов
2) вероятность отказа не менее двух элементов
Решение. Пересечем конус разлета осколков сферой радиуса 50 м и определим математическое ожидание числа осколков, приходящихся на единицу площади поверхности шарового пояса, образовавшегося в результате пересечения конуса разлета со сферой. Обозначим через S площадь поверхности шарового пояса:
Так как общее число осколков N= 100, то математическое ожидание числа их а, приходящегося на единицу площади поверхности шарового пояса, будет
Вероятность попадания данного осколка в данную площадку
11.4. Задачи для самостоятельной работы 11.1. Математическое ожидание числа отказов радиоаппаратуры за 10000 часов работы равно 10. Определить вероятность отказа радиоаппаратуры за 100 часов работы. (Ответ:
11.2. Вероятность того, что любой абонент позвонит на коммутатор в течение часа равна 0,01. Телефонная станция обслуживает 300 абонентов. Какова вероятность, что в течение часа позвонят 4 абонента? (Ответ:
11.3. Аппаратура содержит 2000 одинаково надежных элементов, вероятность отказа для каждого из которых равна р = 0,0005. Какова вероятность отказа аппаратуры, если он наступает при отказе хотя бы одного из элементов? (Ответ: 11.4. В течение часа коммутатор получает в среднем 60 вызовов. Какова вероятность того, что за время 30 сек, в течение которых телефонистка отлучилась, не будет ни одного вызова? (Ответ:
11.5. Вероятность того, что изделие не выдержит испытания, равна 0,001. Найти вероятность того, что из 5000 изделий более чем одно не выдержит испытания. Сравнить результаты расчетов, полученных с использованием распределения Пуассона и с использованием биномиального распределения. В последнем случае расчет производить с помощью семизначных таблиц логарифмов. (Ответ: 1) 0,95958; 2) 0,95963) 11.6. За рассматриваемый период времени среднее число ошибочных соединений, приходящееся на одного телефонного абонента, равно 8. Какова вероятность, что для данного абонента число ошибочных соединений будет больше 4? (Ответ: 0,9)
11.7. Найти вероятность того, что среди 200 изделий окажется более трех бракованных, если в среднем бракованные изделия составляют 1%. (Ответ: 0,143) 11.8. Корректура в 500 страниц содержит 500 опечаток. Найти вероятность того, что на странице не меньше трех опечаток. (Ответ: 11.9. В наблюдениях Резерфорда и Гейгера радиоактивное вещество за промежуток времени 7,5 сек, испускало в среднем 3,87 (Ответ: 0,4)
11.10. Определить асимметрию случайной величины, распределенной по закону Пуассона. (Асимметрией называется отношение (Ответ:
11.11. В аппаратурный отсек космической ракеты за время ее полета попадает
Условная вероятность для каждой из них попасть при этом в уязвимый блок равна р. Найти вероятность попадания в блок: а) ровно k частиц; б) хотя бы одной частицы. (Ответ: а)
11.12. Определить дисперсию числа атомов радиоактивного вещества, распадающегося в единицу времени, если даны масса вещества М, период полураспада Рассеиванием и поглощением частиц пренебречь. Число Авогадро N0 = Периодом полураспада вещества (Ответ:
11.13. Определить вероятность того, что в экран площадью а) ровно десять б) не менее двух если период полураспада вещества Рассеиванием и поглощением частиц пренебречь. Число Авогадро N0 = Периодом полураспада вещества (Ответ: а)
11.14. Доказать, что полиномиальное распределение
где
а
можно аппроксимировать функцией
где (Указание: Представить
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1597; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.102.163 (0.009 с.) |

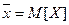 и дисперсия
и дисперсия  случайной величины X, имеющей плотность вероятности
случайной величины X, имеющей плотность вероятности  , вычисляются по формулам
, вычисляются по формулам ,
, .
. определяется формулой
определяется формулой .
. .
. вычисляются по формулам
вычисляются по формулам
 ,
,


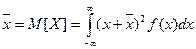
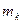 и центральный
и центральный  -го порядка – это числовые характеристики
-го порядка – это числовые характеристики
 ,
, - математическое ожидание
- математическое ожидание  ,
,  - возможные значения случайной величины
- возможные значения случайной величины 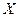 ,
,  - соответствующие им вероятности,
- соответствующие им вероятности,  - математическое ожидание
- математическое ожидание 
 ,
,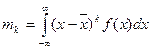
 ,
,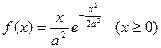 .
. ;
; и
и  .
. целое),
целое), ,
, ,
,
 .
. .
. , получим
, получим .
. , то
, то .
.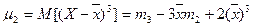 ,
, .
. ,
, , где
, где 
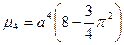 .
. .
.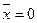 . Срединное отклонение Е вычисляется по формуле
. Срединное отклонение Е вычисляется по формуле .
.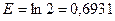 .
.
 ;
;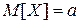 ; б)
; б)  в)
в)  )
)
 )
)
 )
) .
. )
) ,
, - дисперсия угла крена.
- дисперсия угла крена. ;
;  )
) .
. )
)
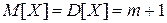 )
)
 )
) )
)
 )
)
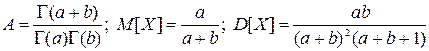 )
) 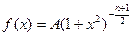 ,
, — целое положительное число, большее 1. Определить постоянную А, математическое ожидание и дисперсию случайной величины X.
— целое положительное число, большее 1. Определить постоянную А, математическое ожидание и дисперсию случайной величины X.
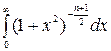 следует воспользоваться подстановкой
следует воспользоваться подстановкой  , приводящей к бета-функции, а последнюю выразить через гамма-функцию)
, приводящей к бета-функции, а последнюю выразить через гамма-функцию) -распределение)
-распределение) ,
, .
. )
) и
и 
 .
.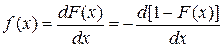 )
) .
.
 является функцией распределения случайного времени поисков
является функцией распределения случайного времени поисков  , необходимого для обнаружения судна)
, необходимого для обнаружения судна) , а вероятность распада ядра любого атома в единицу времени постоянна и равна р.
, а вероятность распада ядра любого атома в единицу времени постоянна и равна р.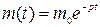
 равна
равна 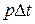 и составить дифференциальное уравнение для m(t))
и составить дифференциальное уравнение для m(t))
 ,
,  время в годах,
время в годах,  .
. , то есть научных работников, имеющих возраст меньше среднего (среди научных работников), больше, чем имеющих возраст больше среднего. Средний возраст среди научных работников
, то есть научных работников, имеющих возраст меньше среднего (среди научных работников), больше, чем имеющих возраст больше среднего. Средний возраст среди научных работников  года)
года) ,
, при
при  .
. при
при 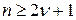 ,
, 
 произвести замену переменных
произвести замену переменных  , приводящей к бета-функции, а последнюю выразить через гамма-функцию)
, приводящей к бета-функции, а последнюю выразить через гамма-функцию)
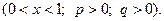
 )
) плотность вероятности
плотность вероятности 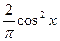 .
. )
)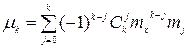 , где
, где  )
) .
. , где
, где  )
) ,
, .
. ,
, .
.



 , где
, где  , получим:
, получим: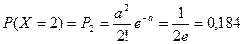 ;
; .
. Пример 11.2. При разрыве баллона в процессе испытания на прочность образовалось 100 осколков, распределившихся равномерно в «конусе разлета», т. е. в области, ограниченной двумя коническими поверхностями с углами 30° и 60° (см. рис.). Найти математическое ожидание и дисперсию числа осколков, приходящихся на 1 м2 части поверхности сферы, находящейся внутри конуса разлета, если радиус сферы 50 м, а центр ее совпадает с точкой разрыва.
Пример 11.2. При разрыве баллона в процессе испытания на прочность образовалось 100 осколков, распределившихся равномерно в «конусе разлета», т. е. в области, ограниченной двумя коническими поверхностями с углами 30° и 60° (см. рис.). Найти математическое ожидание и дисперсию числа осколков, приходящихся на 1 м2 части поверхности сферы, находящейся внутри конуса разлета, если радиус сферы 50 м, а центр ее совпадает с точкой разрыва. м2
м2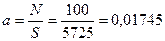 осколка.
осколка. м2 мала(она равна
м2 мала(она равна  , а направления полета осколков взаимно независимы; поэтому можно считать, что случайное число осколков X, приходящееся на 1 м2 поверхности сферы, распределено по закону Пуассона и, следовательно, имеет место равенство
, а направления полета осколков взаимно независимы; поэтому можно считать, что случайное число осколков X, приходящееся на 1 м2 поверхности сферы, распределено по закону Пуассона и, следовательно, имеет место равенство .
. )
) )
) )
) )
) )
) -частицы. Найти вероятность того, что за 1 сек это вещество испустит хотя бы одну
-частицы. Найти вероятность того, что за 1 сек это вещество испустит хотя бы одну  ).
). )
) элементарных частиц с вероятностью
элементарных частиц с вероятностью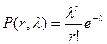 .
. ; б)
; б)  )
) , атомный вес вещества А, число атомов в грамм-атоме
, атомный вес вещества А, число атомов в грамм-атоме  .
. — число атомов в грамм-атоме, т. е. в количестве вещества, вес которого в граммах равен атомному весу.
— число атомов в грамм-атоме, т. е. в количестве вещества, вес которого в граммах равен атомному весу. . Составить дифференциальное уравнение для среднего числа частиц в момент времени
. Составить дифференциальное уравнение для среднего числа частиц в момент времени  . Приравнять среднее число частиц половине первоначального. Полученное в результате этого уравнение дает возможность найти вероятность распада данной частицы; умножая ее на число частиц, получим
. Приравнять среднее число частиц половине первоначального. Полученное в результате этого уравнение дает возможность найти вероятность распада данной частицы; умножая ее на число частиц, получим  )
) см2, поставленный на расстоянии r =5 см перпендикулярно потоку от
см2, поставленный на расстоянии r =5 см перпендикулярно потоку от  лет, масса вещества М — 0,1 г, атомный вес вещества А = 238.
лет, масса вещества М — 0,1 г, атомный вес вещества А = 238. ; б)
; б)  , где
, где  )
)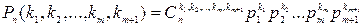 ,
, ,
, ,
, ,
, , если все вероятности
, если все вероятности  ,малы, а
,малы, а  в виде:
в виде: , где
, где  . Так как
. Так как  и
и  конечны, то
конечны, то  )
)


