
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: «Случайные величины и законы их распределения».Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тема: «Случайные величины и законы их распределения». Понятие случайной величины. Перейдем от рассмотрения случайных событий к изучению случайных величин. Ведь, даже в таком простом опыте, как измерение длины отрезка, вообще говоря, мы будем иметь дело и со случайными событиями и со случайными величинами. Проводя многократные измерения этой длины, мы получим серию результатов, отличающихся друг от друга в силу случайных причин (способа расположения линейки, положения глаз наблюдателя, качества обработки поверхностей и т.д.). Получить то или иное значение длины будет являться случайным событием, а само значение длины - случайной величиной. То есть случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств. Это может быть и число больных на приеме у врача, и число студентов на лекции, и величина давления, или температуры у любого из сидящих, например, в лекционной аудитории. Различают дискретные и непрерывные случайные величины. Дискретная случайная величина принимает счетное множество значений (например, число студентов в аудитории, число вызовов врача на дом). Непрерывная случайная величина принимает любые значения внутри некоторого интервала (температура, масса, давление). Каждой случайной величине Дискретная случайная величина. Дискретной (прерывной) называют случайную величину, принимающую некоторые определенные числовые значения. Чтобы задать случайную дискретную величину, надо перечислить ее возможные значения и вероятности, с которыми они достигаются. Закон распределения дискретной случайной величины может быть задан в виде: · таблицы; · графика; · функции распределения. Рассмотрим подробнее каждый из этих способов. Закон распределения в виде таблицы.
Таблица может быть конечной или бесконечной. При этом все вероятности больше нуля. Так как события
График распределения.
График распределения часто называют многоугольником распределения или полигоном частот. Функция распределения.
График функции распределения:
Пример задания функции распределения.
Числовые характеристики дискретной случайной величины. Математическое ожидание. Математическим ожиданием (средним значением) называется сумма произведений всех возможных значений случайной величины на вероятности появления этих значений. Пусть в результате испытаний значение Найдем среднее значение
Математическое ожидание - это то значение, около которого происходит случайный разброс. Дисперсия дискретной случайной величины. Величина разброса (рассеяния) всех возможных значений около математического ожидания измеряется дисперсией.
Свойства дисперсии: 1. Дисперсия постоянной величины равна 0. 2. Если Числовые характеристики непрерывной случайной величины. Математическое ожидание. Не останавливаясь подробно на выводе этой формулы, отметим лишь, что ее легко получить из формулы для математического ожидания дискретной случайной величины, произведя соответствующие замены. От суммирования дискретных значений переходим к интегрированию на отрезке числовой оси. Соответственно суммирование по всем возможным значениям заменяется на интегрирование в пределах
Биномиальное распределение. Пусть производится
где Число сочетаний вычисляется по формуле: причем Таблица биномиального распределения имеет вид:
Числа Пример 1. Вероятность рождения мальчика равна 0,515. Как велика вероятность того, что из 10 наугад выбранных новорожденных будет 6 мальчиков? Предположение о независимости может считаться выполненным. Следовательно, для искомой вероятности имеем
Пример 2. Появление колонии микроорганизмов данного вида в определенных условиях оценивается вероятностью 0,7. Найти вероятность того, что в шести пробах данная колония микроорганизмов появится 4 раза. Решение. Распределение Пуассона. Случайная величина называется распределенной по закону Пуассона, если она принимает счетное множество возможных значений 0, 1, 2... с вероятностями, которые вычисляются по формуле:
Следует отметить, что из всех дискретных распределений, распределение Пуассона встречается чаще других. Оно тесно связано с биномиальным распределением, являясь предельным. Если в биномиальном распределении зафиксировать
Распределение Пуассона затабулировано для различных значений параметра Пример 1. Известно, что в среднем на приеме у врача бывает ежедневно 5 пациентов. Найти вероятности обслуживания в день от 0 до 12 пациентов. Решение:
Нормальное распределение.
Случайная величина называется распределенной по нормальному закону, если она имеет плотность вероятности следующего вида:
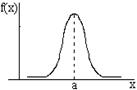
здесь График этой функции приведен на рисунке.
Часто эту кривую называют колоколом за ее форму. Отметим ее основные особенности. Кривая симметрична. Центр симметрии, и это легко доказать, есть точка
Ветви кривой не пересекают ось абсцисс, а лишь асимптотически приближаются к ней, то есть
Исследование заданной функции с помощью производных, а именно нахождение максимума и точек перегиба (что рекомендуется проделать самостоятельно) дает следующие результаты: 1. 2. Координаты точек перегиба
Параметр
Это значит, что площадь под кривой должна сохраняться постоянной, равной единице. Следовательно, если вершина колокола опускается, то ветви будут подниматься. Вот пример двух кривых Гаусса для разных
Математическое ожидание. Вспомним общую формулу для
Подставим вместо
Чтобы взять этот интеграл, введем замену переменной:
Сократив на
Решая первый интеграл, получаем:
При подстановке значений верхнего и нижнего пределов интеграл обращается в ноль. Обратимся ко второму интегралу. Функция вида В результате интегрирования мы пришли к интересному и важному результату: Дисперсия.
Подставляя под интеграл функцию Гаусса и пользуясь только что полученным соотношением
Дисперсия была введена как мера рассеяния всех значений вблизи математического ожидания. Оказалось, что параметр ширины кривой играет ту же роль. Его называют среднеквадратичным отклонением Тема: «Случайные величины и законы их распределения». Понятие случайной величины. Перейдем от рассмотрения случайных событий к изучению случайных величин. Ведь, даже в таком простом опыте, как измерение длины отрезка, вообще говоря, мы будем иметь дело и со случайными событиями и со случайными величинами. Проводя многократные измерения этой длины, мы получим серию результатов, отличающихся друг от друга в силу случайных причин (способа расположения линейки, положения глаз наблюдателя, качества обработки поверхностей и т.д.). Получить то или иное значение длины будет являться случайным событием, а само значение длины - случайной величиной. То есть случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств. Это может быть и число больных на приеме у врача, и число студентов на лекции, и величина давления, или температуры у любого из сидящих, например, в лекционной аудитории. Различают дискретные и непрерывные случайные величины. Дискретная случайная величина принимает счетное множество значений (например, число студентов в аудитории, число вызовов врача на дом). Непрерывная случайная величина принимает любые значения внутри некоторого интервала (температура, масса, давление). Каждой случайной величине
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 733; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.51.35 (0.008 с.) |

 соответствует некоторое множество чисел. Это множество значений, которое может принимать величина
соответствует некоторое множество чисел. Это множество значений, которое может принимать величина  - ее возможные значения. Для полного описания случайной величины кроме множества возможных значений нужно знать как часто случайная величина принимает то или другое из своих значений, то есть вероятность появления данного значения. Обозначим вероятности появления тех или иных значений как:
- ее возможные значения. Для полного описания случайной величины кроме множества возможных значений нужно знать как часто случайная величина принимает то или другое из своих значений, то есть вероятность появления данного значения. Обозначим вероятности появления тех или иных значений как: 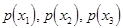 . Л юбое правило, устанавливающее связь между возможными значениями случайной величины и их вероятностями называется законом распределения случайной величины.
. Л юбое правило, устанавливающее связь между возможными значениями случайной величины и их вероятностями называется законом распределения случайной величины.





 попарно несовместны, а их сумма есть событие достоверное (при каждом осуществлении опыта величина
попарно несовместны, а их сумма есть событие достоверное (при каждом осуществлении опыта величина  . Это положение называется условием нормировки.
. Это положение называется условием нормировки.

 ,
,  .
.
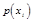

 раз,
раз,  раз и т.д.
раз и т.д.



 - независимые случайные величины, то
- независимые случайные величины, то 
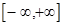 . Вероятность отдельного значения дискретной случайной величины
. Вероятность отдельного значения дискретной случайной величины 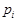 заменим на элемент вероятности для непрерывной случайной величины
заменим на элемент вероятности для непрерывной случайной величины 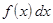 . Тогда получаем:
. Тогда получаем: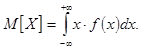
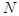 независимых опытов. В каждом опыте с одной и той же вероятностью
независимых опытов. В каждом опыте с одной и той же вероятностью 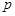 может наступить событие
может наступить событие 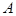 . Случайная величина
. Случайная величина 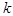 наступлений события
наступлений события  вычисляются по формуле:
вычисляются по формуле: ,
, .
.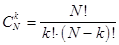 ,
,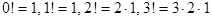 и т. д.
и т. д.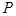

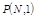
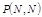
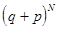 . Отсюда и распределение получило такое название.
. Отсюда и распределение получило такое название.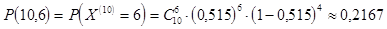 .
.
 ,
,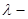 параметр распределения.
параметр распределения.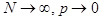 , таким образом, чтобы произведение
, таким образом, чтобы произведение  оставалось постоянным и равным
оставалось постоянным и равным 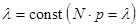 , то получим
, то получим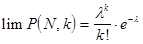 .
. .
.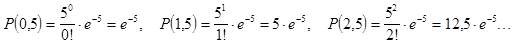
 ,
, постоянные величины, смысл которых станет ясен при дальнейшем рассмотрении. Пока же будем называть их параметрами кривой,
постоянные величины, смысл которых станет ясен при дальнейшем рассмотрении. Пока же будем называть их параметрами кривой, 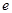 - основание натурального логарифма (
- основание натурального логарифма ( )
)
 . Значит параметр
. Значит параметр  можно назвать центром симметрии. При возрастании величины
можно назвать центром симметрии. При возрастании величины  , кривая, не меняя своей формы будет смещаться вдоль оси абсцисс вправо.
, кривая, не меняя своей формы будет смещаться вдоль оси абсцисс вправо.


 .
.
 часто называют параметром ширины кривой. При возрастании
часто называют параметром ширины кривой. При возрастании 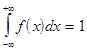


 .
.
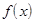 функцию Гаусса:
функцию Гаусса: .
.
 и представив интеграл от суммы функций, как сумму интегралов, имеем:
и представив интеграл от суммы функций, как сумму интегралов, имеем: .
. .
. - есть табличный интеграл.
- есть табличный интеграл. .
. .
.
 измеряются в метрах
измеряются в метрах  , в то время как дисперсия измеряется в метрах квадратных
, в то время как дисперсия измеряется в метрах квадратных  .
.


