
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение случайной величины.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Случайной величиной x называется величина, значение которой заранее предсказать нельзя. Все экономические показатели являются случайными величинами. Это и заработная плата работников, и объем выпуска продукции, и рентабельность, и производительность труда и др. Понятие случайной величины тесно связано с понятием случайного события. Рассмотрим пример: один раз подбрасывают монету. Пусть случайная величина x - число выпадений герба. Эта случайная величина принимает два значения: x = 0, если выпадает «решка» и x = 1, если выпадает «герб».Таким образом, случайная величина принимает свои значения в зависимости от элементарных исходов эксперимента т.е. является функцией от элементарных исходов эксперимента x = f ( т.е. каждое значение случайной величины ставится в соответствие исходу эксперимента. Возможные значения случайной величины будем обозначать малыми буквами латинского алфавита. Поскольку множество исходов эксперимента может быть конечным или бесконечным, то будем рассматривать случайные величины двух типов. Случайная величина x называется случайной величиной дискретного типа, если множество ее возможных значений конечно или счетно. Случайная величина называется случайной величиной непрерывного типа, если ее значения заполняют сплошь некоторый интервал. Рассмотрим сначала дискретные случайные величины. Дискретные случайные величины. Ряд распределения. Рядом распределения или законом распределения случайной величины называется перечень значений случайной величины и соответствующих этим значениям вероятностей. Пусть р(x=а распространяется на все возможные значения k. Пример 11. Монету бросают дважды. Найти ряд распределения числа появлений герба. Здесь x - число появления герба, ряд распределения приведен в Таблице 1. Таблица 1
р р р
Функция распределения. Функцией распределения F(x) называется вероятность того, что случайная величина x примет значение меньше x, где x– любое действительное число, F(x) = р (x < х), где - ¥ < х < ¥ Свойства функции распределения: 1. 0 £ F(x) £ 1 2. При х 3. При х 4. Вероятность попадания случайной величины в произвольный интервал действительной оси [x
Докажем это свойство. Для этого рассмотрим событие (x < х2). Очевидно, что это событие можно записать в виде суммы: (x < х2) = (х1 £ x < х2) + (x < х1), используя формулу сложения для несовместных событий, получим р(x < х2) = р(х1 £ x < х2) + р(x < х1), откуда следует F (х2) = р(х1 £ x < х2) + F (х1) или р(х1 £ x < х2) = F (х2)- F (х1). 5. Функция распределения F (х) – неубывающая функция на всей оси Ох, т.е. если х2 > х1, то F (х2) ³ F (х1). Действительно, пусть х2 > х1 , в пункте 5 показано, что для F (х2) справедливо равенство F (х2) = р(х1 £ x < х2) + F (х1), а так как р(х1 £ x < х2) что F (х2) ³ F (х1). 6. Функция распределения непрерывна слева
Зная закон распределения дискретной случайной величины, можно вычислить функцию распределения по формуле F (x) = где суммирование распространяется на все те значения индекса i, для которых
Пример 12. Построить функцию распределения для случайной величины, рассмотренной в Примере 11. Поскольку функция F(x) определена для всей действительных значений x, то рассмотрим последовательно интервалы: 1. х Î (- ∞; 0], F (x) = р(x < x) = 0, так как событие (x < x) на данном интервале является невозможным событием. 2. х Î (0; 1], F (x) = р(x = 0) = 1/4, здесь неравенству x < x удовлетворяет одно значение x = 0. 3. х Î (1; 2], F (x) = р(x = 0) + P (x = 1) = 1/4 + 1/2 = 3/4,здесь неравенству x < x удовлетворяют два значения x = 0 и x = 1. 4. х Î (2; ∞) F (x) = P (x = 0) + P (x = 1) + P (x = 2) = 1/4 + 1/2 + 1/4 = 1, на этом интервале неравенству x < x удовлетворяют все значения случайной величины. Таким образом, F(x) = График вычисленной функции приведен на Рис.7.
Рис. 7. Квантилью порядка р распределения случайной величины x непрерывного типа называется действительное число x Лекция 7. Числовые характеристики случайной величины. Математическое ожидание. Случайные величины помимо законов распределения могут описываться также числовыми характеристиками. Математическим ожиданием М (x) случайной величины называется ее среднее значение. Математическое ожидание дискретной случайной величины вычисляется по формуле М (x) = где Рассмотрим свойства математического ожидания: 1. Математическое ожидание константы равно самой константе М (С) = С 2. Если случайную величину умножить на некоторое число k, то и математическое ожидание умножится на это же число М (kx) = kМ (x) 3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий М (x1 + x2 + … + xn) = М (x1) + М (x2) +…+ М (xn) 4. М (x1 - x2) = М (x1) - М (x2) 5. Для независимых случайных величин x1, x2, … xn математическое ожидание произведения равно произведению их математических ожиданий М (x1, x2, … xn) = М (x1) М (x2) … М (xn) 6. М (x - М (x)) = М (x) - М (М(x)) = М (x) - М (x) = 0 Вычислим математическое ожидание для случайной величины из Примера 11. М (x) = Пример 12. Пусть случайные величины x1, x2 заданы соответственно законами распределения: x1 Таблица 2
x2 Таблица 3
Вычислим М (x1) и М (x2) М (x1) = (- 0,1) 0,1 + (- 0,01) 0,2 + 0 · 0,4 + 0,01 · 0,2 + 0,1 · 0,1 = 0 М (x2) = (- 20) 0,3 + (- 10) 0,1 + 0 · 0,2 + 10 · 0,1 + 20 · 0,3 = 0 Математические ожидания обеих случайных величин одинаковы- они равны нулю. Однако характер их распределения различный. Если значения x1 мало отличаются от своего математического ожидания, то значения x2 в большой степени отличаются от своего математического ожидания, и вероятности таких отклонений не малы. Эти примеры показывают, что по среднему значению нельзя определить, какие отклонения от него имеют место как в меньшую, так и в большую сторону. Так при одинаковой средней величине выпадающих в двух местностях осадков за год нельзя сказать, что эти местности одинаково благоприятны для сельскохозяйственных работ. Аналогично по показателю средней заработной платы не возможно судить об удельном весе высоко- и низкооплачиваемых работниках. Поэтому, вводится числовая характеристика – дисперсия D (x), которая характеризует степень отклонения случайной величины от своего среднего значения: D (x) = M (x - M (x))2 . (2) Дисперсия –это математическое ожидание квадрата отклонения случайной величины от математического ожидания. Для дискретной случайной величины дисперсия вычисляется по формуле: D (x) = Из определения дисперсии следует, что D (x) Свойства дисперсии: 1. Дисперсия константы равна нулю D (C) = 0 2. Если случайную величину умножить на некоторое число k, то дисперсия умножится на квадрат этого числа D (kx) = k2 D (x) 3. D (x) = М (x2) – М2 (x) 4. Для попарно независимых случайных величин x1, x2, … xn дисперсия суммы равна сумме дисперсий. D (x1 + x2 + … + xn) = D (x1) + D (x2) +…+ D (xn) Вычислим дисперсию для случайной величины из Примера 11. Математическое ожидание М (x) = 1. Поэтому по формуле (3) имеем: D (x) = (0 – 1)2·1/4 + (1 – 1)2·1/2 + (2 – 1)2·1/4 =1·1/4 +1·1/4= 1/2 Отметим, что дисперсию вычислять проще, если воспользоваться свойством 3: D (x) = М (x2) – М2 (x). Вычислим дисперсии для случайных величин x1, x2 из Примера 12 по этой формуле. Математические ожидания обеих случайных величин равны нулю. D (x1) = 0,01· 0,1 + 0,0001· 0,2 + 0,0001· 0,2 + 0,01· 0,1 = 0,001 + 0,00002 + 0,00002 + 0,001 = 0,00204 D (x2) = (-20)2 · 0,3 + (-10)2 · 0,1 + 102 · 0,1 + 202 · 0,3 = 240 +20 = 260 Чем ближе значение дисперсии к нулю, тем меньше разброс случайной величины относительно среднего значения. Величина Модой случайной величины x непрерывного типа Md, называется действительное число, определяемое как точка максимума плотности распределения вероятностей f(x). Медианой случайной величины x непрерывного типа Mn называется действительное число, удовлетворяющее уравнению F(x) = Лекция 8. Примеры дискретных распределений. 1. Биноминальное. Пусть произведено n независимых испытаний. В каждом испытании наступает либо событие А, либо Закон распределения этой случайной величины можно записать следующим образом Р (x = m) = Действительно, рассмотрим выражение (p + q)n =1 , разложим двучлен (p + q)n по формуле бинома Ньютона. Получим т.е. сумма вероятностей значений случайной величины равна единице, следовательно (4) является законом распределения. Найдем математическое ожидание: M (x) = Рассмотрим случайные величины x1, x2, … xn, с одинаковым законом распределения: xk = где k = 1,2,…n. Тогда x = x1 + x2 + … + xn. Используя свойства математического ожидания получим: М (x) = М (x1 + x2 + … + xn) = М (x1) + М (x2) +…+ М (xn). Найдем математическое ожидание xk, М (xk) = 0 · (1 – p) + 1· p = р, тогда М (x) = np Аналогично найдем дисперсию: D (x) = D (x1 + x2 + … + xn) = D (x1) + D (x2) +…+ D (xn) D (xk) = (0 – p)2 (1 – p) + (1 – p)2 p = p2 (1 – p) + (1 – p)2 p = = p (1 – p) (p + 1 – p) = p (1 – p) = p q D (x) = n p q,
2. Распределение Пуассона. Пусть произведено бесконечное число испытаний. Рассмотрим случайную величину x -число появлений события А. m = 0, 1, 2,... Закон распределения в данном случае имеет вид: p (x =m) = Покажем, что сумма вероятностей равна единице.
Аналогично можно показать, что математическое ожидание и дисперсия соответственно равны М (x) = Закон Пуассона называют законом редких событий.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 603; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 ), w Î W,
), w Î W, ) = р
) = р 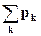 = 1, где суммирование
= 1, где суммирование (x = 0) = р(РР) = 1/2 * 1/2 = 1/4,
(x = 0) = р(РР) = 1/2 * 1/2 = 1/4, (x = 1) = р(ГР + РГ) = Р(ГР) + Р(РГ) = 1/2 * 1/2 + 1/2*1/2= 1/2,
(x = 1) = р(ГР + РГ) = Р(ГР) + Р(РГ) = 1/2 * 1/2 + 1/2*1/2= 1/2, (x =2) = р (ГГ) = 1/2 * 1/2 = 1/4,
(x =2) = р (ГГ) = 1/2 * 1/2 = 1/4, = 1/4 +1/2 + 1/4 = 1.
= 1/4 +1/2 + 1/4 = 1. - ¥ F(x)
- ¥ F(x)  р(х1 £ x < х2) = F (х2) – F (х1)
р(х1 £ x < х2) = F (х2) – F (х1) 0, то отсюда следует,
0, то отсюда следует, .
. ,
, .
.

 , удовлетворяющее уравнению р
, удовлетворяющее уравнению р  = р
= р , (1)
, (1) – значения случайной величины, р i - ихвероятности.
– значения случайной величины, р i - ихвероятности. .
. =
=  (3)
(3) называется среднеквадратическим отклонением. Модой случайной величины x дискретного типа Md называется такое значение случайной величины, которому соответствует наибольшая вероятность.
называется среднеквадратическим отклонением. Модой случайной величины x дискретного типа Md называется такое значение случайной величины, которому соответствует наибольшая вероятность. .
.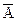 соответственно с вероятностями р, 1 –р. Рассмотрим случайную величину x - число появлений события А в последовательности испытаний.
соответственно с вероятностями р, 1 –р. Рассмотрим случайную величину x - число появлений события А в последовательности испытаний. , m=0,1,2,…n. (4)
, m=0,1,2,…n. (4)
 ,
,

 , λ > 0 - параметр распределения, m = 0, 1, 2,... (5)
, λ > 0 - параметр распределения, m = 0, 1, 2,... (5) .
. ,
,


