
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стохастический эксперимент, пространство элементарных исходовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Исходными понятиями теории вероятностей являются понятия стохастического эксперимента, cлучайного события и вероятности случайного события. Стохастическими называются эксперименты, возможные исходы которых известны, но заранее предугадать, какой из них будет иметь место нельзя. Все возможные исходы эксперимента называют пространством элементарных исходов и обозначают Таким образом, рассматриваемому эксперименту поставлено в соответствие некоторое множество 1. Производится эксперимент: один раз бросают монету. Множество 2. Один раз бросают игральный кубик. Возможные исходы этого эксперимента - выпадение числа очков, равного 1, 2, 3, 4, 5, 6, т.е.
3. Монету бросают дважды,
Здесь ГГ означает,что оба раза появится герб, ГР -при первом бросании появится герб,а при втором –решка, РГ -при первом бросании появится решка, при втором –герб, РР -оба раза появится решка. 3.4. Монету бросают до первого появления герба. Возможные исходы эксперимента: Г -герб выпадет с первого раза, РГ -герб выпадет при втором бросании, РРГ -герб выпадет при третьем бросании и т.д Теоретически эксперимент может продолжаться бесконечно долго. Пространством элементарных событий такого эксперимента является бесконечное множество
4.5. Два лица А и В условились встретиться в интервале времени [ 0,T ]. Обозначим x - время прихода лица А , Y -время прихода лица В.
Геометрически это пространство представляет квадрат, изображенный на Рис.1
Рис.1 Множество Приведенные примеры показывают,что множество Пространство элементарных исходов зависит от условий,, в которых производится случайный эксперимент. В дальнейшем будем рассматривать условия, при которых исходы эксперимента равновозможны, т.е. никакой исход эксперимента не имеет объективного преимущества перед другими. В рассмотренных выше примерах предполагается, что эксперименты производятся в идеальных условиях (идеальная монета бросается на идеально гладкую поверхность и т. д.).
Лекция 2. Определение случайного события. Элементарные исходы эксперимента - это простейшие случайные события и определению не подлежат. Однако в каждом случайном эксперименте кроме элементарных могут происходить и другие случайные события. Так, например, в примере 2 можно рассмотреть события: А - хотя бы один раз появится герб, В - герб появится при первом бросании, С - хотя бы один раз появится решка и т. А - выпадение четного числа очков, В - выпадение числа очков, не меньше 4, С – выпадение нечетного числа очков и т. д. Событие А произойдет, если будет иметь место один из исходов эксперимента ГГ,ГР,РГ.: выпадет число очков, равное 2 или 4 или 6. Таким образом, А = Пусть в примере 3 В примере 3 могут произойти события: А - хотя бы один раз выпадет герб, В - герб выпадет при первом бросании, С - хотя бы один раз выпадет решка и т.д. Здесь А={ ГГ, ГР, РГ }, В={ ГГ,ГР }, С = { РР,РГ,ГР }. Пусть в примере 4 событие А состоит в том, что будет сделано не более трех бросаний. Тогда А = Рассмотрим задачу о встрече (пример 4).Предположим, что каждое из лиц А и В ожидает другого время, не большее чем t, С ={(x, y): (Рис.2).
Рис.2
Итак, случайное событие А – это некоторое подмножество Алгебра событий. Событие называется невозможным, если оно в эксперименте заведомо не наступит и обозначается Если в случайном эксперименте из наступления события А следует наступление события В, то говорят, что А влечет В Если А Суммой двух событий А и В называют событие А + В (А
Рис.3 В примере 2 А + В= { 2, 4, 5, 6 }. Аналогичный смысл имеет сумма любого числа событий. Если I -произвольное множество значений некоторого индекса i, A Произведением двух событий А и B называют событие AВ (А дящее тогда и только тогда, когда происходит и событие А, и событие В (все события А Произведение событий соответствует пересечению множеств, (Рис.4).
Рис.4 Для событий из примера 2 АВ = { 4, 6 }. Разностью А \ В двух событий А и В есть событие, происходящее тогда и только тогда. когда происходит А, но не происходит В. Разность событий соответствует разности множеств, (Рис.5)
Рис.5. В примере 2 А \ В = { 2 }. Событие
Рис.6. В примере 2 Операции сложения и умножения событий обладают следующими свойствами: а) А+В = В+А, АВ = ВА (коммутативность); б) (А+В)+С=А+(В+С ), А(ВС)=(АВ)С (ассоциативность); в) (А+В)С=АС+ВС) (дистрибутивность умножения относительно cложения). Отметим еще некоторые очевидные соотношения: А Два события А и В называются несовместными, если невозможно их совместное наступление, иными словами АВ = Совокупность событий А 1) хотя бы одно из этих событий непременно происходит; 2) любая пара событий несовместна, А Лекция 3. Классическое определение вероятности.
Вероятность – это количественная оценка возможности наступления случайного события. По классическому определению, вероятностью случайного события Р(А) называется отношение числа m благоприятствующих исходов к общему числу n равновозможных исходов эксперимента Р(А) = Классическая вероятность обладает следующими свойствами: 1. Р(А) 2. Вероятность достоверного события Р( 3. Если событие С = А+В, причем А и В несовместны, то Р(С) = Р(А)+Р(В). 4. Вероятность противоположного события Р( 5. Вероятность невозможного события равна нулю Р( 6. Если А 7. Вероятность любого события заключена между нулем и единицей 0 Рассмотрим примеры на вычисление вероятностей. Пример 1. Один раз подбрасывают монету. Чему равна вероятность выпадения герба? Здесь Пример 2. Один раз подбрасывают шестигранный игральный кубик. Чему равна вероятность того, что выпадет число очков, не менее четырех?
В более сложных задачах не представляется возможным наглядно записать все исходы эксперимента, а также благоприятные случайному событию исходы. В таких случаях применяются комбинаторные методы подсчета чисел m и n. Пример 3. В ящике находится 10 деталей, среди которых 3 бракованных. Из ящика наугад извлекают 5 деталей. Найти вероятность того, что среди них окажется две бракованных. Событие А - среди 5-ти извлеченных деталей 2 бракованных, а три доброкачественных. Для подсчета m и n используем правило сочетаний: n = Отметим недостатки классического определения вероятностей: 1.Классическое определение невозможно применить в случае бесконечного пространства элементарных исходов. 2.Существует проблема нахождения разумного способа выделения «равновозможных случаев». Например, как определить вероятность того, что родившийся ребенок окажется мальчиком? По мере развития теории вероятностей появлялись другие определения вероятности, которые устраняли недостатки классического. Эти определения будут рассмотрены немного позже.
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 779; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.21 (0.007 с.) |


 =
=  .
. . Результатом эксперимента является один и только один исход. Рассмотрим примеры.
. Результатом эксперимента является один и только один исход. Рассмотрим примеры.
 , где буква Г означает появление герба, буква Р -появление решки.
, где буква Г означает появление герба, буква Р -появление решки.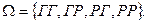



 = { 2, 4, 6 }, В = { 4, 5, 6 }, C = { 1, 3, 5 }.
= { 2, 4, 6 }, В = { 4, 5, 6 }, C = { 1, 3, 5 }. .
. <t < Т. Пусть С-событие, состоящее в том, что встреча произойдет. Тогда
<t < Т. Пусть С-событие, состоящее в том, что встреча произойдет. Тогда }
}
 Те элементарные исходы, при которых событие А наступает, называют благоприятствующими событию А.
Те элементарные исходы, при которых событие А наступает, называют благоприятствующими событию А. Событие называется достоверным, если оно в эксперименте заведомо наступит и обозначается
Событие называется достоверным, если оно в эксперименте заведомо наступит и обозначается  В).
В). В), происходящее тогда и только тогда, когда происходит или событие А, или событие В. Сумма событий соответствует объединению множеств, Рис.3.
В), происходящее тогда и только тогда, когда происходит или событие А, или событие В. Сумма событий соответствует объединению множеств, Рис.3.

 -некоторое множество событий то сумма есть событие,происходящее тогда и только тогда, когда происходит хотя бы одно событие.
-некоторое множество событий то сумма есть событие,происходящее тогда и только тогда, когда происходит хотя бы одно событие. В), происхо-
В), происхо- ).
).

 называется противоположным событию А, если оно происходит тогда и только тогда, когда не происходит А (соответствует дополнению множеств) Рис. 6.
называется противоположным событию А, если оно происходит тогда и только тогда, когда не происходит А (соответствует дополнению множеств) Рис. 6.
 , А
, А  ,
,  ,
,  .
. .Примером несовместных событий являются А и
.Примером несовместных событий являются А и  ,А
,А  , …, А
, …, А  составляет полную группу попарно несовместных событий, если:
составляет полную группу попарно несовместных событий, если: =
=  i
i  j, i,j=
j, i,j=  .
.
 0.
0. равна
равна Р(В).
Р(В). , причем исходы эксперимента равновозможны, А={ Г }, таким образом m =1, n =2, P(A) =
, причем исходы эксперимента равновозможны, А={ Г }, таким образом m =1, n =2, P(A) =  .
. -равновозможны, А={4,5,6}, m =3, n =6, P(A) =
-равновозможны, А={4,5,6}, m =3, n =6, P(A) =  .
. , P(A) =
, P(A) =  =
=  =
=  .
.


