
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы комбинаторики. Пространство элементарныхСодержание книги
Поиск на нашем сайте
Событий. Определения вероятности
Элементы комбинаторики Пусть дано множество, состоящее из n различных элементов Две различные перестановки состоят из одних и тех же элементов, но отличаются порядком следования элементов. Пример 1.1. Имеется четыре вакантных должности и четыре претендента на эти должности. Сколькими способами можно заполнить эти должности? Решение. Р 4 = 4! = 24. Размещением на множестве из n элементов по m элементов называется любое упорядоченное подмножество, содержащее m элементов. Два размещения считаются различными, если они состоят из различных элементов, или состоят из одних и тех же элементов, но отличаются порядком следования элементов в наборе. Число размещений на множестве из n элементов по m элементов определяется формулой Пример 1.2. Сколькими способами можно рассадить по 3 студента за стол в группе из 20 студентов? Решение. Сочетанием на множестве из n элементов по m элементов называется всякое неупорядоченное подмножество, содержащее m элементов. Два различных сочетания отличаются хотя бы одним элементом. Число сочетаний на множестве из п элементов по т элементов определяется формулой Пример 1.3. В ящике 5 деталей. Сколькими способами из ящика можно взять 3 детали? Решение. Классическое определение вероятности. Элементарным событием или исходом называется всякая возможная реализация эксперимента. Множество
где п – общее число исходов; т – число исходов, благоприятствующих появлению события А. Пример 1.4. В группе 8 юношей и 5 девушек. Из группы случайным образом отбирается 5 студентов. Найти вероятность того, что среди них окажется 4 девушки. Решение. Пусть событие А состоит в том, что из 5 случайно отобранных студентов окажутся 4 девушки. Общее число исходов будет равно количеству способов, сколькими из 13 студентов можно отобрать по 5 студентов Геометрическое определение вероятности. Пусть указана область W, из которой наугад выбирается точка. Вероятность того, что выбранная точка одновременно попадет в область А (А Ì W) пропорциональна мере области А (длине, площади, объему): Пример 1.5. Случайно поставленная точка принадлежит квадрату со стороной 4. Найти вероятность того, что она попадет в круг, вписанный в этот квадрат. Решение. Пусть событие А состоит в том, что случайно поставленная точка попадет в круг, вписанный в квадрат. Тогда Статистическое определение вероятности. Пусть некоторый эксперимент повторяют п раз, в результате этого событие А наступило т раз. Относительной частотой
Если число испытаний неограниченно увеличивать, то относительная частота события «стремится» к вероятности наступления события А. Поэтому при статистическом определении вероятности полагают
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.116 (0.005 с.) |

 . Перестановкой на множестве из n элементов называется всякое упорядоченное множество, состоящее из этих n элементов. Число перестановок на множестве из n элементов Рn определяется по формуле
. Перестановкой на множестве из n элементов называется всякое упорядоченное множество, состоящее из этих n элементов. Число перестановок на множестве из n элементов Рn определяется по формуле  .
.
 .
. .
. .
. всех элементарных событий называется пространством элементарных событий. Любое подмножество пространства элементарных исходов называется случайным событием. Исход vi благоприятствует событию А, если появление исхода vi влечет появление события А. Вероятность события характеризует степень объективной возможности наступления этого события. Вероятностью Р(А) события А называется отношение числа исходов, благоприятствующих появлению события А, к общему числу равновозможных исходов.
всех элементарных событий называется пространством элементарных событий. Любое подмножество пространства элементарных исходов называется случайным событием. Исход vi благоприятствует событию А, если появление исхода vi влечет появление события А. Вероятность события характеризует степень объективной возможности наступления этого события. Вероятностью Р(А) события А называется отношение числа исходов, благоприятствующих появлению события А, к общему числу равновозможных исходов. ,
, . Благоприятствовать событию А будут те исходы, в которых будет 4 девушки и 1 юноша
. Благоприятствовать событию А будут те исходы, в которых будет 4 девушки и 1 юноша  . Тогда
. Тогда  .
. . Понятие геометрической вероятности обобщает классическое определение вероятности на случай опытов с бесконечным числом исходов.
. Понятие геометрической вероятности обобщает классическое определение вероятности на случай опытов с бесконечным числом исходов. .
.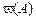 события А называется отношение количества испытаний, в которых наступило событие А, к общему числу проведенных испытаний:
события А называется отношение количества испытаний, в которых наступило событие А, к общему числу проведенных испытаний: .
.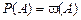 .
.


