
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема повторных одинаковых независимых испытанийСодержание книги
Поиск на нашем сайте (схема Бернулли)
Формула Бернулли Если производится n независимых испытаний, в результате которых могут быть только два исхода А или Если в каждом из n независимых испытаний вероятность появления события А постоянна (равна р) и отлична от 0 и 1, то вероятность того, что в n испытаниях событие А произойдет ровно m раз, определяется по формуле Бернулли
Пример 4.1. Прибор состоит из четырех узлов. Вероятность безотказной работы в течение смены для каждого узла равна 0,8. Узлы выходят из строя независимо друг от друга. Найти вероятность того, что в течение смены откажут ровно два узла. Решение. Из условия задачи
Локальная и интегральная теоремы Муавра–Лапласа Локальная теорема Муавра–Лапласа. Если вероятность появления события А в каждом из независимых испытаний постоянна (равна р) и отлична от 0 и 1, а число испытаний п достаточно велико, то вероятность того, что в п независимых испытаниях событие наступит ровно т раз приближенно определяется по формуле:
где Функция Пример 4.2. Вероятность того, что автомат выпускает стандартную деталь равна 0,9. Какова вероятность того, что из 400 выпущенных автоматом деталей 356 окажутся стандартными. Решение. Из условия задачи р = 0,9; п = 400; т = 356; q = 1– p =
Интегральная теорема Муавра–Лапласа. Если вероятность р наступления события А в каждом из независимых испытаний постоянна и отлична от 0 и 1, а число испытаний велико, товероятность того, что в п независимых испытаниях событие А появится от т1 до т2 раз определяется по формуле
где
Функция Лапласа является нечетной функцией:
Значения функции Лапласа берут из таблицы по найденным значениям х. Пример 4.3. Вероятность реализации одной акции некоторой компании равна 0,8. Брокерская фирма предлагает 100 акций этой компании. Какова вероятность того, что будет продано не менее 70 и не более 85 акций. Решение. По условию задачи п = 100, т1 = 70, т2 = 85, р = 0,8. Находим Поэтому
Формула Пуассона Если в схеме Бернулли п велико, а вероятность появления события р мала, то вероятность того, что в п испытаниях событие наступит ровно т раз определяется по формуле
Формулу Пуассона обычно применяют, если р < 0,01; п >100 и пр £ 10. Пример 4.4. При массовом производстве шестерен вероятность брака равна 0,002. Найти вероятность того, что из 500 выпущенных шестерен будет ровно 2 бракованных. Решение. По условию задачи п =500 и т = 2, р = 0,002, l = пр =
Случайные величины Понятие случайной величины Случайной величиной (СВ) называется числовая функция
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.48.226 (0.006 с.) |

 с неизменными вероятностями
с неизменными вероятностями 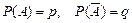 , то такая схема испытаний называется схемой Бернулли.
, то такая схема испытаний называется схемой Бернулли.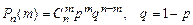 .
. . Используя формулу Бернулли, получим
. Используя формулу Бернулли, получим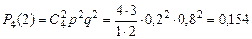 .
.
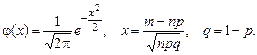
 является четной функцией:
является четной функцией:  . Для функции
. Для функции  ,
,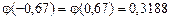 ,
, .
.
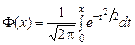 – функция Лапласа,
– функция Лапласа,


 ,
,  .
.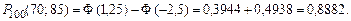
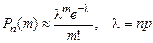 .
. .
.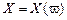 , заданная на пространстве элементарных исходов W и такая, что для любого действительного числа х определена вероятность
, заданная на пространстве элементарных исходов W и такая, что для любого действительного числа х определена вероятность 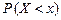 . Случайная величина – это величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно. Различают два вида СВ: дискретные и непрерывные. Дискретная СВ – это величина, которая принимает счетное или конечное число значений. Непрерывной СВ на интервале (a; b) называют СВ, которая может принять любое значение из (a; b). Чтобы задать СВ нужно задать закон распределения. Закон распределения дискретной СВ – это соответствие между возможными значениями СВ и вероятностями их появления. Закон распределения дискретной СВ записывается в виде таблицы:
. Случайная величина – это величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно. Различают два вида СВ: дискретные и непрерывные. Дискретная СВ – это величина, которая принимает счетное или конечное число значений. Непрерывной СВ на интервале (a; b) называют СВ, которая может принять любое значение из (a; b). Чтобы задать СВ нужно задать закон распределения. Закон распределения дискретной СВ – это соответствие между возможными значениями СВ и вероятностями их появления. Закон распределения дискретной СВ записывается в виде таблицы: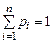 .
.


