
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условные вероятности. Независимость событий.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В ряде случав приходится рассматривать вероятности событий при условии, что имело место некоторое другое событие. Такие вероятности называются условными и обозначаются Р(А / В). Пример. Брошены две игральные кости.Чему равна вероятность того,что сумма выпавших очков равна 8, если известно, что эта сумма является четным числом? Пусть А – сумма выпавших очков равна 8, В – сумма выпавших очков четное число. Найдем сначала безусловную вероятность Р(А) по классическому определению. Число всех возможных исходов эксперимента n =6 (2,6), (3,5), (4,4), (5,3), (6,2). Таким образом m =5 и Р(А) = Теперь вычислим вероятность события А при условии, что наступило событие В. В этом случае возможные исходы эксперимента составляют комбинации, при которых сумма выпавших очков- четное число, таких комбинаций – 18, поэтому m = 5, n = 18, а условная вероятность Р(А / В) = Два события А и В называются независимыми, если наступление одного из них не влияет на вероятность наступления другого, иными словами, если условная вероятность равна безусловной, Р(А / В) = Р(А). В противном случае события считают зависимыми. Так, в приведенном выше примере, события А и В являются зависимыми. События А Рассмотрим пример. Тетраэдр,три грани которого окрашены соответственно в красный, зеленый и синий цвета, а четвертая грань содержит все три цвета, бросается наудачу на плоскость. События А, В, С состоят в том, что тетраэдр упал на грань, содержащую соответственно красный, зеленый либо синий цвет. Безусловные вероятности Р(А) = Р(В) = Р(С) = условные вероятности Р(А/В) = Р(А/С) = Р(В/С) = Р(С/А) = Р(В/А) = Следовательно попарно события - независимы, однако Р(А/ВС) = 1, а это свидетельствует о том,что в совокупности события - зависимы. Рассмотрим формулы, которые используються для вычисления вероятностей сложных событий. Сложным событием называется наблюдаемое событие, выраженное через другие наблюдаемые в том же эксперименте события с помощью допустимих алгебраических операций. Формула сложения. Для произвольных событий А и В справедливо соотношение Р(А+В) = Р(А) + Р(В) - Р(АВ) Для произвольного конечного числа событий формулы сложения имеет вид: Р(А Для несовместных событий вероятность суммы событий равна сумме вероятностей этих событий, т.е. Р(А Формула умножения. Для произвольных событий А и В Р(АВ) = Р(А) Р(B/A)=P(B)P(A/B. Формула справедлива, если Р(А) > 0, P(B) > 0, и позволяет вычислять вероятность совместного осуществления событий А и В в тех случаях, когда условная вероятность считается известной (из дополнительных опытов) или определяется методом вспомогательного эксперимента. Для произвольного конечного числа событий формула умножения имеет вид: Р(А Для независимых в совокупности событий вероятность произведения событий равна произведению их вероятностей, т.е. Р(А Пример 4. В условиях эксперимента, рассмотренного в примере 3 найти вероятности того, что среди выбранных изделий содержатся: а) не более одного бракованного; б) хотя бы одно бракованное. Пусть событие А - среди выбранных изделий не более одного бракованного, Рассмотрим события: А А Тогда А = А Р(А Р(А) = Пусть событие В – среди выбранных изделий хотя бы одно бракованное. Можно решить эту задачу с помощью формулы сложения, но решение будет значительно проще, если перейти к противоположному событию
Пример 5. Определить вероятность того, что выбранное наудачу изделие является первосортным, если известно, что 5% всей продукции является браком, а 80% небракованных изделий удовлетворяют требованиям 1-го сорта. Обозначим А – выбранное изделие является небракованным, В – выбранное изделие удовлетворяет требованиям 1-го сорта, тогда АВ – выбранное изделие является первосортным, а искомая вероятность Р(АВ) = Р(А)Р(В/А) = здесь Р(А) = 1 – 0,05, Р(В/А) = 0,8.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.41.109 (0.008 с.) |

 6=36, а сумма очков, равная 8, выпадет в следующих комбинациях:
6=36, а сумма очков, равная 8, выпадет в следующих комбинациях: .
. .
. ,А
,А  , …, А
, …, А  называются независимыми в совокупности, если для любого А
называются независимыми в совокупности, если для любого А  из их числа и любого подмножества данной совокупности, событие А
из их числа и любого подмножества данной совокупности, событие А  ,
, .
. )-…- Р(А
)-…- Р(А  А
А  )+…+Р(А
)+…+Р(А  А
А  Р(А
Р(А  - среди выбранных изделий - ни одного бракованного,
- среди выбранных изделий - ни одного бракованного,
 =
=  =
=  , Р(А
, Р(А  =
=  =
=  ,
,
 - среди выбранных изделий нет бракованных.
- среди выбранных изделий нет бракованных.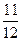
 ,
,


